《数据结构》课程PPT教学课件（2012）第5章 数组和广义表 Arrays & Lists（2/2）

第5章 数组和广义表(Arrays&Lists) 数组和广义表的特点： 表中元素也是一个线性表，即广义的线性表 5.1数组的定义 5.2数组的顺序表示和实现 5.3 矩阵的压缩存储 5.4广义表的定义 5.5 广义表的存储结构 1

1 第5章 数组和广义表（Arrays & Lists） 5.1 数组的定义 5.2 数组的顺序表示和实现 5.3 矩阵的压缩存储 5.4 广义表的定义 5.5 广义表的存储结构 数组和广义表的特点： 表中元素也是一个线性表，即广义的线性表

5.3矩阵的压缩存储 重点介绍稀疏矩阵的压缩和相应的操作。 做加减操作时 很方便 一、稀疏矩阵的压缩存储 有4种压缩方式：线性表、 十字链表、三元组表、 带辅助向量的三元组表 做转置操作时 很方便 二、稀疏矩阵的操作 2

2 5.3 矩阵的压缩存储 重点介绍稀疏矩阵的压缩和相应的操作。 一、稀疏矩阵的压缩存储 二、稀疏矩阵的操作 有4种压缩方式：线性表、十字链表、三元组表、 带辅助向量的三元组表 做加减操作时 很方便 做转置操作时 很方便

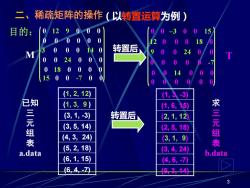
二、稀疏矩阵的操作（以转置运算为例） 目的： 1012900 0 15 0 000 0 0 00014 M 0 转置后 00240 0 0 018000 0 1500-7 0 0 (1,2,12) (1,3 -3} 已知 (1,3,9) (1,6,15】 求 三元组 (3,1,3) 转置后 (2,1,12) (3,5,14) (2,5,18) 三元组 (4,3,24) 3,1,9】 (5,2,18) a.data (3,4,24) b.data (6,1,15) (4,6,-7 (6,4,-Z 344

3 二、稀疏矩阵的操作 0 12 9 0 0 0 0 0 0 0 0 0 -3 0 0 0 14 0 0 0 24 0 0 0 0 18 0 0 0 0 15 0 0 -7 0 0 0 0 –3 0 0 15 12 0 0 0 18 0 9 0 0 24 0 0 0 0 0 0 0 -7 0 0 14 0 0 0 0 0 0 0 0 0 (1, 2, 12) (1, 3, 9 ) (3, 1, -3) (3, 5, 14) (4, 3, 24) (5, 2, 18) (6, 1, 15) (6, 4, -7) (1, 3, -3) (1, 6, 15) (2, 1, 12) (2, 5, 18) (3, 1, 9) (3, 4, 24) (4, 6, -7) (5, 3, 14) 已知 三 元 组 表 a.data 求 三 元 组 表 b.data 转置后 M T （以转置运算为例） 目的： 转置后

有两种实现 压缩转置 转置的方法 快速（压缩）转置 压缩转置的思路：反复扫描a表（记为a.data)y中的 列序，从=1~n依次进行转置。 快速转置的思路：依次把a.data中的元素直接送入b.data 的恰当位置上（即a.data三元组的p指针不回溯）。 关键：怎样寻找b.data的"恰当”位置？

4 有两种实现 转置的方法 压缩转置 快速(压缩)转置 压缩转置的思路：反复扫描a表（记为a.data）中的 列序，从j=1～n依次进行转置。 快速转置的思路：依次把a.data中的元素直接送入b.data 的恰当位置上（即a.data三元组的p指针不回溯）。 关键：怎样寻找b.data的“恰当”位置？

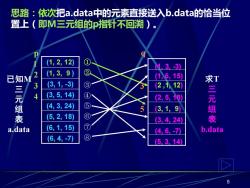
思路：依次把a.data中的元素直接送入b.data的恰当位 置上（即M三元组的指针不回溯）。 (1,2,12) M,3.3 已知M 2 (1,3,9) ② (16,15) (3,1,3) ③ 2,1,12 是 4 (3,5,14) ④ (2,5,18) 组表 (4,3,24) ⑤ 3,1,9) 求三元组表 (5,2,18) ⑥ (3,4,24 a.data (6,1,15) ⑦ 46,-70 data (6,4,-7) ⑧ 5,3,14

5 已知M 三 元 组 表 a.data 求T 三 元 组 表 b.data ③ (1, 3, -3) ① (2 ,1, 12) ⑥ (2, 5, 18) ② (3, 1, 9) ⑧ (4, 6, -7) ④ (5, 3, 14) ⑦ (1, 6, 15) ⑤ (3, 4, 24) (1, 2, 12) (1, 3, 9 ) (3, 1, -3) (3, 5, 14) (4, 3, 24) (5, 2, 18) (6, 1, 15) (6, 4, -7) 思路：依次把a.data中的元素直接送入b.data的恰当位 置上（即M三元组的p指针不回溯）。 p 1 2 3 4 q 3 5

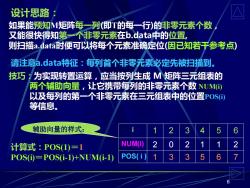
设计思路 如果能预知M矩阵每一列（即T的每一行）的非零元素个数 又能很快得知第一个非零元素在b.data中的位置， 则扫描a.data时便可以将每个元素准确定位（因已知若干参考点） 请注意a.data特征：每列首个非零元素必定先被扫描到。 技巧：为实现转置运算，应当按列生成M矩阵三元组表的 两个辅助向量，让它携带每列的非零元素个数NUM⑥ 以及每列的第一个非零元素在三元组表中的位置P0S) 等信息。 辅助向量的样式： 3 计算式：POS1)=1 POS(i)=POS(i-1)+NUM(i-1) POS( 6

6 如果能预知M矩阵每一列(即T的每一行)的非零元素个数， 又能很快得知第一个非零元素在b.data中的位置, 则扫描a.data时便可以将每个元素准确定位(因已知若干参考点) 技巧：为实现转置运算，应当按列生成 M 矩阵三元组表的 两个辅助向量，让它携带每列的非零元素个数 NUM(i) 以及每列的第一个非零元素在三元组表中的位置POS(i) 等信息。 设计思路： i 1 2 3 4 5 6 NUM(i) 2 0 2 1 1 2 POS( i ) 1 3 3 5 6 7 计算式：POS(1)＝1 POS(i)＝POS(i-1)+NUM(i-1) 辅助向量的样式： 请注意a.data特征：每列首个非零元素必定先被扫描到

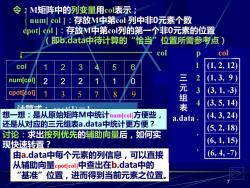
令 ?M矩阵中的列变量用col表示： num[col]:存放M中第col列中非0元素个数 pot[col]:存放M中第col列的第一个非0元素的位置 即b.data中待计算的”恰当”位置所需参考点) col col 5 6 1 (1,2,12 num[col] 2 三元 2 (1,3,9 3 Q 3 (3,1,-3) L竺H 表 (3,5,14) 41N 想一想：是从原始矩阵M中统计numfcoll方便些 a.data (4,3,24 还是从对应的三元组表a.data中统计更方便？ (5,2,18) 讨论：求出按列优先的铺助向量后，如何实 现快速转置？ (6,1,15) 由a.data中每个元素的列信息，可以直接 (6,4,-7 从辅助向量epotcoll中查出在b.data中的 “基准”位置，进而得到当前元素之位置

7 令：M矩阵中的列变量用col表示； num[ col ]：存放M中第col 列中非0元素个数 cpot[ col ]：存放M中第col列的第一个非0元素的位置 （即b.data中待计算的“恰当”位置所需参考点） 讨论：求出按列优先的辅助向量后，如何实 现快速转置？ col 1 2 3 4 5 6 num[col] 2 2 2 1 1 0 cpot[col] 1 计算式： cpot(1)＝1 cpot[col]＝ cpot[col-1] + num[col-1] 3 5 7 8 9 0 12 9 0 0 0 0 0 0 0 0 0 -3 0 0 0 14 0 0 0 24 0 0 0 0 18 0 0 0 0 15 0 0 -7 0 0 M col 1 2 3 4 5 6 由a.data中每个元素的列信息，可以直接 从辅助向量cpot[col]中查出在b.data中的 “基准”位置，进而得到当前元素之位置。 三 元 组 表 a.data (6, 4, -7) (6, 1, 15) (5, 2, 18) (4, 3, 24) (3, 5, 14) (3, 1, -3) (1, 3, 9 ) (1, 2, 12) p col 1 2 3 4 . . . 想一想：是从原始矩阵M中统计num[col]方便些， 还是从对应的三元组表a.data中统计更方便？

快速转置算法描述： Status FastTransposeSMatrix (TSMatirx M,TSMatirx &T) 前3个for循环 /M是顺序存储的三元组表，求M的转置矩阵钉 用来产生两个 T.mu Mnu ;T.nu=M.mu T.tu M.tu; 辅助向量 f(Tt血)4 for(col片1；col<=M.nu;col++)numcol]=O;/W先清0再统计每列非零元素个数 for(i=1;i<=M.tu;i++){col =M.data[i]j;+num [col]; cpos[1 ]=1; /再生成每列首元位置辅助向量 for(col=2;col <=M.nu;col++)cpos[col]=cpos[col-1]+num [col-1]; for(p=1;p<=M.tu;p+)77p指向a.data,循环次数为菲0元素总个数 {eol=M.datalp.j;g=cpos fdol];/查辅助向量得q,即T中位置 T.data[ql.i=M.data[p].j; T.data[ql.j=M.data[p].i; 元素转置 T.data[g].value=M.data[p].value; +cpos col]; //for 重要！修改向量内容（列坐标加1)，预 }1/if 备给同列的下一非零元素定位之用 return OK; }//FastTranposeSMatrix; 8

8 Status FastTransposeSMatrix（TSMatirx M, TSMatirx &T） { T.mu = M.nu ;T .nu = M.mu ; T.tu = M.tu ; if ( T.tu ) { for(col = 1; col <=M.nu; col++) num[col] =0; for( i = 1; i <=M.tu; i ++) {col =M.data[i] .j ; ++num [col] ;} cpos[ 1 ] =1; for(col = 2; col <=M.nu; col++) cpos[col ]=cpos[col-1]+num [col-1 ] ; for( p =1; p <=M.tu ; p ++ ) { col =M.data[ p ]. j ; q =cpos [ col ]; T.data[q].i = M.data[p]. j; T.data[q].j = M.data[p]. i; T.data[q]. value = M.data[p]. value; + + cpos[col] ; } //for } //if return OK; } //FastTranposeSMatrix; 快速转置算法描述： //M是顺序存储的三元组表，求M的转置矩阵T //先清0再统计每列非零元素个数 //再生成每列首元位置辅助向量 //p指向a.data，循环次数为非0元素总个数 tu //查辅助向量得q，即T中位置 前3个for循环 用来产生两个 辅助向量 重要！修改向量内容（列坐标加1），预 备给同列的下一非零元素定位之用 元素转置

快速转置算法的效率分析： 1.与常规算法相比，附加了生成辅助向量表的工作。增开了2 个长度为列长的数组(m[和cpos]) 2.从时间上，此算法用了4个并列的单循环，而且其中前3个 单循环都是用来产生辅助向量表的。 for(col=1;col<=M.nu;col+){};循环次数=nu(列数)： for(i=1;i<=M.tu;i+){); 循环次数=tu(非0元素个数)： for(col片2；col<=M.nu;col+){};循环次数=nu; for(p1;p<=Mtu;p+){};八循环次数=tu; 该算法的时间复杂度=nu+tu+nu+tu=O(nu+tu) 讨论：最恶劣情况是矩阵中全为非零元素，此时tu=nu*mu 而此时的时间复杂度也只是O(mu*nu),并未超过传统转置 算法的时间复杂度。 小结传统转置：O(mu*n四 压缩转置：O(mu*tu) 压缩快速转置：O(nu+tu) 增设辅助向量，牺牲空间 稀疏矩阵相乘的算法略， 效率换取时间效率。 见教材P101-103

9 1. 与常规算法相比，附加了生成辅助向量表的工作。增开了2 个长度为列长的数组(num[ ]和cpos[ ]）。 传统转置：O(mu*nu) 压缩转置：O(mu*tu) 压缩快速转置：O(nu+tu) 快速转置算法的效率分析： 2. 从时间上，此算法用了4个并列的单循环，而且其中前3个 单循环都是用来产生辅助向量表的。 for(col = 1; col <=M.nu; col++){ }; 循环次数＝nu（列数）; for( i = 1; i <=M.tu; i ++) { }; 循环次数＝tu （非0元素个数）; for(col = 2; col <=M.nu; col++) { }; 循环次数＝nu; for( p =1; p <=M.tu ; p ++ ) { }; 循环次数＝tu; 该算法的时间复杂度＝nu+tu+nu+tu=O(nu+tu） 讨论：最恶劣情况是矩阵中全为非零元素，此时tu=nu*mu 而此时的时间复杂度也只是O(mu*nu)，并未超过传统转置 算法的时间复杂度。 小结： 稀疏矩阵相乘的算法略， 见教材P101-103 增设辅助向量，牺牲空间 效率换取时间效率

5.4六义表的定义 1、定义日 广义表是线性表的推广，也称为列表(sts) 记为： a1,a2 a 广义表名表头(Head) 表尾(Tail) n是表长 在广义表中约定： ①第一个元素是表头，而其余元素组成的表称为表尾： ②用小写字母表示原子类型，用大写字母表示列表。 讨论：广义表与线性表的区别和联系？ 广义表中元素既可以是原子类型，也可以是列表； 当每个元素都为原子且类型相同时，就是线性表。 10

10 5.4 广义表的定义 广义表是线性表的推广，也称为列表（lists） 记为： LS = ( a1 , a2 , .， an ) 广义表名 表头(Head） 表尾 (Tail) 1、定义： ① 第一个元素是表头，而其余元素组成的表称为表尾； ② 用小写字母表示原子类型，用大写字母表示列表。 n是表长 在广义表中约定： 讨论：广义表与线性表的区别和联系？ 广义表中元素既可以是原子类型，也可以是列表； 当每个元素都为原子且类型相同时，就是线性表