《数据结构》课程PPT教学课件（2015）第7章 图（上）

《数据结构》 第七章图（上）

《 数据结构》 第七章 图(上)

数据结构 第七章图 7.1图的定义和术语 7.2图的存储结构 7.2.1数组表示法 7.2.2邻接表 7.3图的遍历 7.3.1深度优先搜索 7.3.2广度优先搜索 7.4图的连通性问题 7.4.3最小生成树 7.5有向无环图及其应用 7.5.1拓扑排序 7.6最短路径 7.6.1从某个源点到其余各顶点的最短路径 7.6.2每一对顶点之间的最短路径

数据结构 tjm 第七章 图 7.1 图的定义和术语 7.2 图的存储结构 7.2.1 数组表示法 7.2.2 邻接表 7.3 图的遍历 7.3.1 深度优先搜索 7.3.2 广度优先搜索 7.4 图的连通性问题 7.4.3 最小生成树 7.5 有向无环图及其应用 7.5.1 拓扑排序 7.6 最短路径 7.6.1 从某个源点到其余各顶点的最短路径 7.6.2 每一对顶点之间的最短路径

数据结构 7.1图的定义和术语 圜的定义：是一种多对多的结构关系，每个元素 可以有零个或多个直接前趋；零个或多个直接后 继。图是由顶点集合(vertex)及顶点间的关系集 合组成的一种数据结构： Graph=(V,R) 其中 V={v|v∈某个数据对像} 是顶点的有穷非空集合； R=VR}={(V,w)IV,w∈V} 图的类型定义参见P156

数据结构 tjm 图的类型定义参见P156 7.1 图的定义和术语 图的定义：是一种多对多的结构关系，每个元素 可以有零个或多个直接前趋；零个或多个直接后 继。图是由顶点集合(vertex)及顶点间的关系集 合组成的一种数据结构： Graph＝( V, R ) 其中 V = { v | v  某个数据对象} 是顶点的有穷非空集合； R ={VR}={(v, w) | v, w  V }

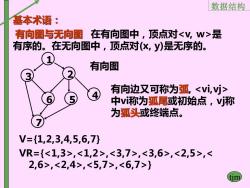
数据结构 基本术语： 有向图与无向图在有向图中，顶点对是 有序的。在无向图中，顶点对(x,y)是无序的。 有向图 有向边又可称为弧， 中V称为狐尾或初始点，Vj称 为狐头或终端点。 V={1,2,3,4,5,6,7} VR={,,,,,,,,}

数据结构 tjm 基本术语： 有向图与无向图 在有向图中，顶点对是 有序的。在无向图中，顶点对(x, y)是无序的。 5 3 6 7 2 1 4 有向图 V={1,2,3,4,5,6,7} VR={,,,,,,,,} 有向边又可称为弧, 中vi称为狐尾或初始点，vj称 为狐头或终端点

数据结构 无向图 V={1,23,4,5,6,7} VR={(1,3),(3,4),(4,5),(1,2).(2,6),(2,7).(6,7), (5,6),(1,5).(1,7)}

数据结构 tjm 无向图 5 3 6 7 2 1 4 V={1,2,3,4,5,6,7} VR={(1,3),(3,4),(4,5),(1,2),(2,6),(2,7),(6,7), (5,6),(1,5),(1,7) }

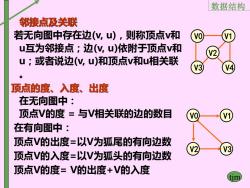
数据结构 邻接点及关联 若无向图中存在边(N,u),则称顶点V和 u互为邻接点；边(V,u)依附于顶点V和 V2 u;或者说边(N,u)和顶点V和u相关联 顶点的度、入度、出度 在无向图中： 顶点V的度=与V相关联的边的数目 vo 在有向图中： 顶点V的出度=以V为狐尾的有向边数 顶点V的入度=以V为狐头的有向边数 顶点V的度=V的出度+V的入度

数据结构 tjm 邻接点及关联 若无向图中存在边(v, u)，则称顶点v和 u互为邻接点；边(v, u)依附于顶点v和 u；或者说边(v, u)和顶点v和u相关联 。 顶点的度、入度、出度 在无向图中： 顶点V的度 = 与V相关联的边的数目 在有向图中： 顶点V的出度=以V为狐尾的有向边数 顶点V的入度=以V为狐头的有向边数 顶点V的度= V的出度+V的入度 V0 V3 V4 V1 V2 V0 V1 V2 V3

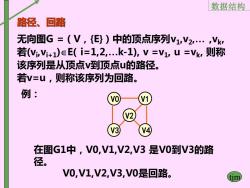
数据结构 路径、回路 无向图G=（V,{E})中的顶点序列V1V2·Vk, 若(V,V+1)∈E(i=1,2,.k-1),V=V1,u=Vk,则称 该序列是从顶点V到顶点u的路径。 若V=u,则称该序列为回路。 例： V3 在图G1中，V0,V1,V2,V3是V0到V3的路 径。 V0,V1,V2,V3,V0是回路

数据结构 tjm 路径、回路 无向图G =（V，{E}）中的顶点序列v1 ,v2 ,. ,vk , 若(vi ,vi+1)E( i=1,2,.k-1), v =v1 , u =vk , 则称 该序列是从顶点v到顶点u的路径。 若v=u，则称该序列为回路。 在图G1中，V0,V1,V2,V3 是V0到V3的路 径。 V0,V1,V2,V3,V0是回路。 V0 V3 V4 V1 V2 例：

数据结构 有向图G=(V,{E))中的顶点序列V1V2,.Vk, 若∈E(i=1,2,.k-1),V=V,u=Vk,则 称该序列是从顶点V到顶点u的路径。 若V=u,则称该序列为回路。 例： 有向图G2 在图G2中，V0,V2,V3是V0到V3的路径 V0,V2,V3,V0是▣路

数据结构 tjm 有向图G2 V0 V1 V2 V3 在图G2中，V0,V2,V3 是V0到V3的路径 。 V0,V2,V3,V0是回路。 有向图G =（V，{E}）中的顶点序列v1 ,v2 ,. ,vk , 若E (i=1,2,.k-1), v =v1 , u =vk , 则 称该序列是从顶点v到顶点u的路径。 若v=u，则称该序列为回路。 例：

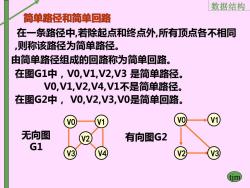
数据结构 简单路径和简单回路 在一条路径中，若除起点和终点外，所有顶点各不相同 ,则称该路径为简单路径。 由简单路径组成的回路称为简单回路。 在图G1中，V0,V1,V2,V3是简单路径。 V0,V1,V2,V4,V1不是简单路径。 在图G2中，V0,V2,V3,V0是简单回路。 0 无向图 V2 有向图G2 G1 13 V3

数据结构 tjm 在一条路径中,若除起点和终点外,所有顶点各不相同 ,则称该路径为简单路径。 由简单路径组成的回路称为简单回路。 在图G1中，V0,V1,V2,V3 是简单路径。 V0,V1,V2,V4,V1不是简单路径。 在图G2中， V0,V2,V3,V0是简单回路。 无向图 G1 有向图G2 V0 V3 V4 V1 V2 V0 V1 V2 V3 简单路径和简单回路

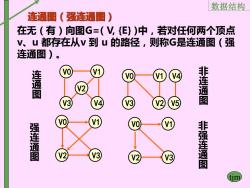
数据结构 连通图（强连通图） 在无（有)向图G=(V,{})中，若对任何两个顶点 V、u都存在从V到u的路径，则称G是连通图（强 连通图) 。 连通图 非连通图 强连通图 V3 非强连通图

数据结构 tjm 非 连 通 图 连 通 图 强 连 通 图 非 强 连 通 图 V0 V1 V2 V3 V0 V3 V4 V1 V2 V0 V1 V2 V3 V0 V3 V2 V1 V5 V4 连通图（强连通图） 在无（有）向图G=( V, {E} )中，若对任何两个顶点 v、u 都存在从v 到 u 的路径，则称G是连通图（强 连通图）