《互换性与测量技术》课程教学资源（教案讲义）第二章几何量测量基础

互换性与测量技术课程教案第二次课次授课方式|理论课讨论课口实验课口习腿课口 其他口课时2（请打√）安排授课题目（教学章、节或主题）：第二章几何量测量基础S2-1概述S2-1概述S2-2长度、角度量值的传递$2-3计量器具和测量方法$2-4测量误差2-5各类测量误差的处理教学目的、要求（分掌握、熟悉、了解三个层次）：掌握测量技术的基本知识；熟悉计量器具与测量方法、测量误差分类；了解计量单位与量值的传递。了解等精度测量列的数据处理方法。教学重点及难点：教学重点：量块的组合使用；误差的处理方法教学难点：随机误差的处理方法及步骤；教学基本内容方法及手段采用多媒体和黑板相第二章几何量测量基础结合的教学手段。通过一、概述实例讲解量块的组合使、长度基准用。通过补充概率等内三、量块容说明随机误差的分布四、计量器具和测量方法规律。五、测量误差随机误差的处理可六、数据误差和处理结合例题分析讲解。作业、讨论题、思考题：1.测量的实质是什么？一个完整的测量过程应包括哪几个要素？2.量块的分等和分级的？3.什么是测量误差？测量误差有几种表示形式4.随机误差的能消除吗？应怎样对它处理？

1 互换性与测量技术 课程教案 课次 第二次 授课方式 （请打√） 理论课 讨论课□ 实验课□ 习题课□ 其他□ 课时 安排 2 授课题目（教学章、节或主题）： 第二章 几何量测量基础 §2-1 概述 §2-1 概述 §2-2 长度、角度量值的传递 §2-3 计量器具和测量方法 §2-4 测量误差 §2-5 各类测量误差的处理 教学目的、要求（分掌握、熟悉、了解三个层次）： 掌握测量技术的基本知识；熟悉计量器具与测量方法、测量误差分类；了解计量单位 与量值的传递。了解等精度测量列的数据处理方法。 教学重点及难点： 教学重点：量块的组合使用;误差的处理方法 教学难点：随机误差的处理方法及步骤； 教 学 基 本 内 容 方法及手段 第二章 几何量测量基础 一、概述 二、长度基准 三、量块 四、计量器具和测量方法 五、测量误差 六、数据误差和处理 采用多媒体和黑板相 结合的教学手段。通过 实例讲解量块的组合使 用。通过补充概率等内 容说明随机误差的分布 规律。 随机误差的处理可 结合例题分析讲解。 作业、讨论题、思考题： 1．测量的实质是什么？一个完整的测量过程应包括哪几个要素？ 2. 量块的分等和分级的？ 3. 什么是测量误差？测量误差有几种表示形式 4．随机误差的能消除吗？应怎样对它处理？ √

基本教材和主要参考资料：《几何量公差与检测》第九版甘永立主编上海科学技术出版社出版；参考教材：《互换性与技术测量》胡凤兰高等教育出版社《几何量公差与检测习题集》甘永立主编上海科学技术出版社出版。课后小结：1、了解测量的基础知识，理解检测的意义，掌握精度测量的基本概念和测量过程的四要素;2、了解计量单位与量值的传递，量块的相关知识；掌握量块的使用方法3、测量方法分类；掌握测量误差与数据处理的方法。第二章 几何量测量基础课次：2本章为一般讲解，要求学生基本掌握。因为在误差理论与数据处理课程中已经讲过。基本内容：概述：检测的意义、测量的基本要素、检测的一般步骤;计量单位与量值传递：长度单位及其基准、量块、长度的量值传递；测量器具与测量方法：测量器具的分类、测量器具的技术性能指标、 测量方法分类;测量误差：测量误差及表达式、误差的分类、误差的来源及减小其影响的措施、测量不确定度、测量数据的处理。81概述为了保证机械零件的互换性，需要对完工零件的几何量进行检测，以判断是否符合设计要求。、几何量测量的定义几何量测量是指为确定被测几何量的量值而进行的实验过程本质是将被测几何量与作为计量单位的标准量进行比较，从而确定两者比值的过程二、测量要素

2 基本教材和主要参考资料： 《几何量公差与检测 》第九版 甘永立 主编 上海科学技术出版社出版； 参考教材：《互换性与技术测量》 胡凤兰 高等教育出版社 《几何量公差与检测习题集》甘永立 主编 上海科学技术出版社出版。 课后小结： １、了解测量的基础知识，理解检测的意义，掌握精度测量的基本概念和测 量过程的四要素； ２、了解计量单位与量值的传递，量块的相关知识；掌握量块的使用方法 ３、测量方法分类；掌握测量误差与数据处理的方法。 第二章 几何量测量基础 课次：2 本章为一般讲解，要求学生基本掌握。因为在误差理论与数据处理课程中已经讲过。 基本内容： 概述：检测的意义、测量的基本要素、检测的一般步骤； 计量单位与量值传递：长度单位及其基准、量块、长度的量值传递； 测量器具与测量方法：测量器具的分类、测量器具的技术性能指标 、 测量方法分类； 测量误差：测量误差及表达式、误差的分类、误差的来源及减小其影响的措施、测量 不确定度、测量数据的处理。 §1 概述 为了保证机械零件的互换性，需要对完工零件的几何量进行检测，以判断是否符合设计 要求。 一、几何量测量的定义 几何量测量是指为确定被测几何量的量值而进行的实验过程。 本质是将被测几何量与作为计量单位的标准量进行比较，从而确定两者比值的过程。 二、测量要素

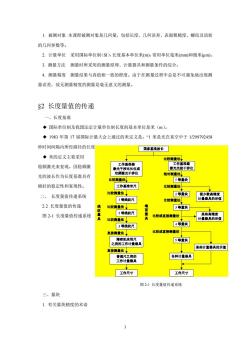
1．被测对象本课程被测对象是几何量，包括长度、几何误差、表面粗糙度、螺纹及齿轮的几何参数等。2.计量单位采用国际单位制(SI),长度基本单位米(m),常用单位毫米(mm)和微米(um)。3.测量方法测量时所采用的测量原理、计量器具和测量条件的综合。4．测量精度测量结果与真值相一致的程度。由于在测量过程中总是不可避免地出现测量误差，故无测量精度的测量是毫无意义的测量。82长度量值的传递一、长度基准◆国际单位制及我国法定计量单位制长度的基本单位是米（m）。1983年第17届国际计量大会上通过的米定义是：1米是光在真空中于1/299792458秒时间间隔内所经路径的长度国家基准波长●米的定义主要采用比较测量法无先装车部仪无仪限稳频激光来复现。因稳频激双频激光干涉仪绝对测量法光的波长作为长度基准具有比较测量法等量块极好的稳定性和复现性工作基准米尺比较测量法比较测量法2等量块二、长度量值传递系统计量卷具的示值■等线纹尺教测量法2.2长度量值的传递比较测量法、3等量块2等线纹尺高料图2-1长度量值传递系统比较或直接测量针整费具的示值比较测量法等量块等线纹尺比较或直接测量法直接测量法！5等量块之美南机床用零具其些计量器具的示值直接测量各种计量器具禁耀升芝类工作尺寸 工件尺寸图2-1长度量值传递系统三、量块1.有关量块精度的术语

3 1. 被测对象 本课程被测对象是几何量，包括长度、几何误差、表面粗糙度、螺纹及齿轮 的几何参数等。 2. 计量单位 采用国际单位制（SI），长度基本单位米(m)，常用单位毫米(mm)和微米(μm)。 3. 测量方法 测量时所采用的测量原理、计量器具和测量条件的综合。 4. 测量精度 测量结果与真值相一致的程度。由于在测量过程中总是不可避免地出现测 量误差，故无测量精度的测量是毫无意义的测量。 §2 长度量值的传递 一、长度基准 ◆ 国际单位制及我国法定计量单位制长度的基本单位是米（m）。 ◆ 1983 年第 17 届国际计量大会上通过的米定义是：“1 米是光在真空中于 1/299792458 秒时间间隔内所经路径的长度”。 ◆ 米的定义主要采用 稳频激光来复现。因稳频激 光的波长作为长度基准具有 极好的稳定性和复现性。 二、 长度量值传递系统 2.2 长度量值的传递 图 2-1 长度量值传递系统 图 2-1 长度量值传递系统 三、量块 1. 有关量块精度的术语 国家基准波长 工作基准器 激光光波干涉仪 工作基准器 激光干涉比长仪或 双频激光干涉仪 比较测量法 1 等量块 绝对测量法 比较测量法 2 等量块 3 等量块 4 等量块 极少数高精度 比较测量法 计量器具的示值 比较或直接测量法 5 等量块 比较或直接测量法 某些高精度 计量器具的示值 某些计量器具的示值 各种计量器具 工件尺寸 端 面 量 具 比较测量法 工作基准米尺 1 等线纹尺 比较测量法 2 等线纹尺 比较测量法 3 等线纹尺 比较测量法 精密机床用尺 之类的工作计量器具 直接测量法 普通尺之类的 工作计量器具 工作尺寸 直接测量法 线 纹 量 具

图2-2有关量块长度、偏差和误差的术语①量块长度1量块一个测量面上的任意点到与其相对的另一测量面相研合的辅助体表面之间的垂直距离。②量块的中心长度1。对应于量块未研合测量面中心点的量块长度。③量块标称长度Ia标记在量块上，用以表明其与主单位（m）之间关系的量值，也称为量块长度的示值。④任意点的量块长度偏差e任意点的量块长度与标称长度的代数差，即e=-ln。合格条件：-t<es+t③量块的长度变动量v量块测量面上任意点中的最大量块长度Imx与最小量块长度Imin之差。合格条件：V≤tv③量块测量面的平面度误差 fa包容量块测量面的实际表面且距离为最小的两个平行平面之间的距离。其公差为ta。合格条件：fa<ta2.量块的精度等级（1）量块的分级按照JG146-2003《量块检定规程》的规定，量块的制造精度分为五级：K、0、1、2、3级，其中K级精度最高，精度依次降低，3级最低。量块生产企业大都按“级"向市场销售量块。（2）量块的分等按照JG146-2003《量块检定规程》的规定，量块的检定精度分为五等：1、2、3、4、5等，其中1等最高，精度依次降低，5等最低。（3）量块按“等"使用与按“级"使用量块按“级"使用时，应以量块的标称长度作为工作尺寸，包含制造误差。量块按“等"使用时，以检定给出的量块中心长度的实际尺寸作为工作尺寸，排除制造误差的影响，仅包含检

4 图 2-2 有关量块长度、偏差和误差的术语 ① 量块长度 l 量块一个测量面上的任意点到与其相对的另一测量面相研合的辅助体表 面之间的垂直距离。 ② 量块的中心长度 lc 对应于量块未研合测量面中心点的量块长度。 ③ 量块标称长度 ln 标记在量块上，用以表明其与主单位（m）之间关系的量值，也称 为量块长度的示值。 ④ 任意点的量块长度偏差 e 任意点的量块长度与标称长度的代数差，即 e=l-ln。合格条 件： -te≤e≤+te。 ⑤ 量块的长度变动量 ν 量块测量面上任意点中的最大量块长度 lmax 与最小量块长度 lmin 之差。合格条件：ν≤tν ⑥ 量块测量面的平面度误差 fd 包容量块测量面的实际表面且距离为最小的两个平行 平面之间的距离。其公差为 td。合格条件：fd≤td 。 2. 量块的精度等级 （1）量块的分级 按照 JJG 146-2003《量块检定规程》的规定，量块的制造精度分为五级：K、0、1、2、3 级，其中 K 级精度最高，精度依次降低，3 级最低。量块生产企业大都按“级”向市场销售量 块。 （2）量块的分等 按照 JJG 146-2003《量块检定规程》的规定，量块的检定精度分为五等：1、2、3、4、5 等，其中 1 等最高，精度依次降低，5 等最低。 （3）量块按“等”使用与按“级”使用 量块按“级”使用时，应以量块的标称长度作为工作尺寸，包含制造误差。量块按“等”使用 时，以检定给出的量块中心长度的实际尺寸作为工作尺寸，排除制造误差的影响，仅包含检

定的测量误差。故量块按“等"使用的测量精度比量块按“级"使用时高。3.量块的组合使用量块具有研合性，故可将不同尺寸的量块进行组合而形成所需的工作尺寸。表2-1列出了国产83块量块组的尺寸系列。量块组合时，为减少量块组合的累积误差，应力求使用最少的块数，一般不超过4块。组成量块时，可从消去所需工作尺寸的最小尾数开始，逐一选取。如为了得到工作尺寸为38.785mm的量块组，从83块一套的量块中选取过程如下：38.785mm-）1.005mm第一块量块37.780mm-）1.28mm第二块量块36.500mm-）6.5mm第三块量块30.000mm第四块量块83计量器具和测量方法一、计量器具的分类计量器具按其本身的结构特点进行分类可分为：量具、量规、计量仪器和计量装置等四类。1.量具以固定形式复现量值的计量器具。2．量规没有刻度的专用计量器具，如检验孔、轴实际尺寸和形状误差的综合结果所用的光滑极限量规。3.计量仪器能将被测几何量的量值转换成可直接观测的指示值（示值）或等效信息的计量器具（量仪）。：为确定被测几何量量值所必需的计量器具和辅助设备的总体。4.计量装置二、计量器具的基本技术性能指标计量器具的基本技术性能指标是合理选择和使用计量器具的重要依据。1.标尺刻度间距标尺刻度间距是指计量器具标尺或分度盘上相邻两刻线中心之间的距离或圆弧长度。2.标尺分度值5

5 定的测量误差。故量块按“等”使用的测量精度比量块按“级”使用时高。 3. 量块的组合使用 量块具有研合性，故可将不同尺寸的量块进行组合而形成所需的工作尺寸。表 2-1 列出了 国产 83 块量块组的尺寸系列。 量块组合时，为减少量块组合的累积误差，应力求使用最少的块数，一般不超过 4 块。组 成量块时，可从消去所需工作尺寸的最小尾数开始，逐一选取。如为了得到工作尺寸为 38.785mm 的量块组，从 83 块一套的量块中选取过程如下： 38.785mm -）1.005mm 第一块量块 37.780mm -）1.28 mm 第二块量块 36.500mm -）6.5 mm 第三块量块 30.000mm 第四块量块 §3 计量器具和测量方法 一、计量器具的分类 计量器具按其本身的结构特点进行分类可分为：量具、量规、计量仪器和计量装置等四类。 1. 量具 以固定形式复现量值的计量器具。 2. 量规 没有刻度的专用计量器具，如检验孔、轴实际尺寸和形状误差的综合结果所用 的光滑极限量规。 3.计量仪器 能将被测几何量的量值转换成可直接观测的指示值（示值）或等效信息的计 量器具（量仪）。 4. 计量装置 为确定被测几何量量值所必需的计量器具和辅助设备的总体。 二、计量器具的基本技术性能指标 计量器具的基本技术性能指标是合理选择和使用计量器具的重要依据。 1. 标尺刻度间距 标尺刻度间距是指计量器具标尺或分度盘上相邻两刻线中心之间的距 离或圆弧长度。 2. 标尺分度值

标尺分度值是指计量器具标尺或分度盘上每一刻度间距所代表的量值。一般长度计算的计量器具的分度值有0.1mm、0.05mm0.02mm、0.01mm、0.005mm、0.002mm0.001mm等几种。例如图2-5中机械比较仪的分度值为0.002mm3.分辨力计量器具所能显示的最末一位数所代表的量值。4.标尺示值范围标尺示值范围是指计量器具所能显示或指示的被测几何量起始值到终止值的范围。图2-5机械比较仪的部分性能指标量块：2-被测工作5.计量器具测量范围计量器具在允许的误差限内所能测出的被测几何量量值的下限值到上限值的范围。测量范围上限值与下限值之差称为量程6.灵敏度计量器具对被测几何量变化的响应变化能力。若被测几何量的变化为Ax，该5-岁几何量引起计量器具的响应变化能力为AL，则灵敏度S为：2-1当上式中分子和分母为同种量时，灵敏度也称做为放大比或放大倍数7.示值误差计量器具的示值与被测几何量的真值的代数差8．修正值、为了消除或减少系统误差，用代数法加到未修正测量结果上的数值。其大小与示值误差的绝对值相等，而符号相反。9.测量重复性在相同的测量条件下，对同一被测几何量进行多次测量时，各测量结果之间的一致性。10.不确定度由于测量误差的存在而对被测几何量量值不能肯定的程度。三、测量方法的分类1.按实测几何量是否为被测几何量分类直接测量被测几何量的数值直接由计量器具读出。间接测量由实测几何量的量值按一定的函数关系式运算后获得。2.按示值是否为被测几何量的量值分类绝对测量计量器具显示或指示的示值即是被测几何量的量值。相对测量（比较测量）计量器具显示或指示出被测几何量相对于已知标准量的偏差，被

6 标尺分度值是指计量器具标尺或分度盘上 每一刻度间距所代表的量值。一般长度计算 的计量器具的分度值有 0.1mm、0.05mm、 0.02mm、0.01mm、0.005mm、0.002mm、 0.001mm 等几种。例如图 2-5 中机械比较仪 的分度值为 0.002mm。 3. 分辨力 计量器具所能显示的最末一位数所 代表的量值。 4. 标尺示值范围 标尺示值范围是指计量器具 所能显示或指示的被测几何量起始值到终止值的 范围。 图 2-5 机械比较仪的部分性能指标 1-量块；2-被测工件 5. 计量器具测量范围 计量器具在允许的误差限内所能测出的被测几何量量值的下限值 到上限值的范围。测量范围上限值与下限值之差称为量程。 6. 灵敏度 计量器具对被测几何量变化的响应变化能力。若被测几何量的变化为 Δx，该 几何量引起计量器具的响应变化能力为 ΔL，则灵敏度 S 为： 2-1 当上式中分子和分母为同种量时，灵敏度也称做为放大比或放大倍数。 7. 示值误差 计量器具的示值与被测几何量的真值的代数差。 8. 修正值 为了消除或减少系统误差，用代数法加到未修正测量结果上的数值。其大小 与示值误差的绝对值相等，而符号相反。 9. 测量重复性 在相同的测量条件下，对同一被测几何量进行多次测量时，各测量结果 之间的一致性。 10. 不确定度 由于测量误差的存在而对被测几何量量值不能肯定的程度。 三、测量方法的分类 1. 按实测几何量是否为被测几何量分类 直接测量 被测几何量的数值直接由计量器具读出。 间接测量 由实测几何量的量值按一定的函数关系式运算后获得。 2. 按示值是否为被测几何量的量值分类 绝对测量 计量器具显示或指示的示值即是被测几何量的量值。 相对测量（比较测量） 计量器具显示或指示出被测几何量相对于已知标准量的偏差，被 x L S   =

测几何量的量值为已知标准量与该偏差值的代数和。3.按被测表面与计量器具测头是否接触分类接触测量测量时计量器具的测头与被测表面接触，并有机械作用的测量力。例如用机械比较仪测量轴径。非接触测量测量时计量器具的测头不与被测表面接触。4.按是否多个被测几何量一起测量分类单项测量分别对工件上的各被测几何量进行独立测量。综合测量同时测量工件上几个相关几何量的综合效应或综合指标，以判断综合结果是否合格。84测量误差一、测量误差的基本概念6=x-x01.绝对误差被测几何量的量值与其真值之差，即(2-3)8一绝对误差；x一测得量值；xo一真值。被测几何量的真值可以用下式来表示：0=x±0(2-4) 测量误差的绝对值越小，则测量结果就越接近真值，因此测量精度就越高。绝对误差适用于评定或比较大小相同的被测几何量的测量精度。2.相对误差相对误差是指绝对误差（取绝对值）与真值之比。因真值无法得到，故实际中常以测得值代替真值进行计算，即(2-5) -6xx相对误差是一个无量纲的数值，通常用百分比表示。如测两孔直径大小分别为50.86mm和20.97mm，其绝对误差分别为+0.02mm和+0.01mm，则由上式得到它们的相对误差分别为fi=0.02/50.86=0.0393%，fz=0.01/20.97=0.0477%，故前者测量精度比后者高。二、测量误差的来源1．计量器具的误差计量器具本身所具有的误差，包括计量器具的设计、制造和使用过程中的各项误差，这些误差的总和反映在示值误差和测量的重复性上。2.方法误差测量方法不完善（包括计算公式不准确，测量方法选择不当等）引起的误囍3．环境误差测量时环境条件不符合标准的测量条件所引起的测量误差。如环境温度V

7 测几何量的量值为已知标准量与该偏差值的代数和。 3. 按被测表面与计量器具测头是否接触分类 接触测量 测量时计量器具的测头与被测表面接触，并有机械作用的测量力。例如用机 械比较仪测量轴径。 非接触测量 测量时计量器具的测头不与被测表面接触。 4. 按是否多个被测几何量一起测量分类 单项测量 分别对工件上的各被测几何量进行独立测量。 综合测量 同时测量工件上几个相关几何量的综合效应或综合指标，以判断综合结果是 否合格。 §4 测量误差 一、测量误差的基本概念 1. 绝对误差 被测几何量的量值与其真值之差，即: (2-3) δ—绝对误差； x—测得量值； x0—真值。 被测几何量的真值可以用下式来表示： (2-4) 测量误差的绝对值越小，则测量结果就越接近真值，因此测量精度就越高。 绝对误差适用于评定或比较大小相同的被测几何量的测量精度。 2. 相对误差 相对误差是指绝对误差（取绝对值）与真值之比。因真值无法得到，故实际中常以测得值 代替真值进行计算，即 (2-5) 相对误差是一个无量纲的数值，通常用百分比表示。如测两孔直径大小分别为 50.86mm 和 20.97mm，其绝对误差分别为+0.02mm 和+0.01mm，则由上式得到它们的相对误差分别为 f1=0.02 /50.86=0.0393%，f2=0.01/20.97=0.0477% ，故前者测量精度比后者高。 二、测量误差的来源 1. 计量器具的误差 计量器具本身所具有的误差，包括计量器具的设计、制造和使用过 程中的各项误差，这些误差的总和反映在示值误差和测量的重复性上。 2. 方法误差 测量方法不完善（包括计算公式不准确，测量方法选择不当等）引起的误 差。 3. 环境误差 测量时环境条件不符合标准的测量条件所引起的测量误差。如环境温度、 0  = x − x x0 = x   x x f   =  

湿度等不符合标准引起的测量误差4.人员误差测量人员人为引起的测量误差。如，测量人员使用计量器具不正确、测量瞄准不准确等。三、 测量误差的分类1.系统误差在相同测量条件下，多次测取同一量值时，绝对值和符号均保持不变的测量误差，或在测量条件改变时，按某一规律变化的测量误差。前者称为定值系统误差，后者称为变值系统误差。2.随机误差在相同测量条件下，多次测取同一量值时，绝对值和符号以不可预定的方式变化着的测量误差。随机误差主要由测量过程中一些偶然性因素或不确定因素引起的。对于连续多次重复测量来说，随机误差符合一定的概率统计规律，故可使用概率论和数理统计的方法来对它进行处理3．粗大误差超出在规定条件下预计的测量误差。含有粗大误差的测得值称为异常值，其数值比较大。粗大误差的产生有主观和客观两方面的原因。由于粗大误差明显歪曲测量结果，故应根据判别粗大误差的准则设法将其剔除。四、测量精度的分类正确度反映测量结果中系统误差的影响程度。若系统误差小，则正确度高。精密度反映测量结果中随机误差的影响程度。它是指连续多次测量所得值之间相互接近的程度。若随机误差小，则精密度高。准确度反映测量结果中系统误差和随机误差的综合影响程度。若系统误差和随机误差者小，则准确度高。(b)正确度高(a)精密度高(c)准确度高(d)准确度低图 2-9精密度、正确度和准确度s5各类测量误差的处理测量列:是指对被测几何量进行连续多次的重复测量得到的测量数据，对其进行数据处理，可提高测量精度。80

8 湿度等不符合标准引起的测量误差。 4. 人员误差 测量人员人为引起的测量误差。如，测量人员使用计量器具不正确、测量 瞄准不准确等。 三、 测量误差的分类 1. 系统误差 在相同测量条件下，多次测取同一量值时，绝对值和符号均保持不变的测 量误差，或在测量条件改变时，按某一规律变化的测量误差。前者称为定值系统误差，后者 称为变值系统误差。 2. 随机误差 在相同测量条件下，多次测取同一量值时，绝对值和符号以不可预定的方 式变化着的测量误差。随机误差主要由测量过程中一些偶然性因素或不确定因素引起的。对 于连续多次重复测量来说，随机误差符合一定的概率统计规律，故可使用概率论和数理统计 的方法来对它进行处理。 3. 粗大误差 超出在规定条件下预计的测量误差。含有粗大误差的测得值称为异常值， 其数值比较大。粗大误差的产生有主观和客观两方面的原因。由于粗大误差明显歪曲测量结 果，故应根据判别粗大误差的准则设法将其剔除。 四、测量精度的分类 正确度 反映测量结果中系统误差的影响程度。若系统误差小，则正确度高。 精密度 反映测量结果中随机误差的影响程度。它是指连续多次测量所得值之间相互接近 的程度。若随机误差小，则精密度高。 准确度 反映测量结果中系统误差和随机误差的综合影响程度。若系统误差和随机误差都 小，则准确度高。 (a)精密度高 (b)正确度高 (c)准确度高 (d)准确度低 图 2-9 精密度、正确度和准确度 §5 各类测量误差的处理 测量列:是指对被测几何量进行连续多次的重复测量得到的测量数据，对其进行数据处理， 可提高测量精度

、测量列中随机误差的处理1.随机误差的特性及分布规律8, =X -Xo重复测量N次，得到测量列的测得值为x1、x2、0,=X2-X0XN设不包含系统误差和粗大误差，被测几何量的真值为xo。则ON=XN-Xo可得出相应各次测得值的随机误差分别为右式。通过对大量的测试实验数据进行统计后发现，多数随机误差服从正态分布规律。正态分布曲线如图2-10所示（横坐标8表示随机误差，纵坐标y表示随机误差的概率密度），它具有如下四13个基本特性：单峰性对称性图2-10正态分布曲线有界性抵偿性正态分布曲线的数学表达式为(2-6)V2元式中，y-一概率密度；标准偏差：—一随机误差。随机误差的标准偏差可用下式计算得到：+++8(2-7)0N式中N-测量列中各测得值的随机误差。测量次数：81、82、.、标准偏差是反映测量列数值分散程度的一项指标，是测量列中单次测量值（任一测得值）的标准偏差。由概率论可知，随机误差区间落在（-8～+8）之间的概率为82P=yds=]doJ-8g/2元2g2化成标准正态分布为2p(t) =-['exp]V2元2表2-2四个特殊t值对应的概率

9 一、测量列中随机误差的处理 1. 随机误差的特性及分布规律 重复测量 N 次，得到测量列的测得值为 x1、x2、.、xN。 设不包含系统误差和粗大误差，被测几何量的真值为 x0。则 可得出相应各次测得值的随机误差分别为右式。 通过对大量的测试实验数据进行统计后发现， 多数随机误差服从正态分布规律。正态分布曲线 如图 2-10 所示（横坐标 δ 表示随机误差，纵坐 标 y 表示随机误差的概率密度），它具有如下四 个基本特性: 单峰性 对称性 图 2-10 正态分布曲线 有界性 抵偿性 正态分布曲线的数学表达式为 (2-6) 式中，y——概率密度；——标准偏差；δ——随机误差。 随机误差的标准偏差 可用下式计算得到： (2-7) 式中 N ——测量次数；δ1、δ2、.、δN ——测量列中各测得值的随机误差。 标准偏差 是反映测量列数值分散程度的一项指标，是测量列中单次测量值（任一测得 值）的标准偏差。 由概率论可知，随机误差区间落在（-δ～+δ）之间的概率为 化成标准正态分布为 表 2-2 四个特殊 t 值对应的概率 0 2 2 0 1 1 0 x x x x x x N = N − = − = −             = − 2 2 2 exp 2π 1    y N N 2 2 2 2  1    + + + =    + − + −         = = −          d 2 exp 2π 1 d 2 2 P y          = − t t t t 0 2 d 2 exp 2π 1 ( )

而测量次数一般不超过几十次，随机误差不超出的概率超出的概率超出±3α的情况实际上很难出现。因此，可取8=±3α作为随机误差的极限值，记0.68260.31740m=±3g(2-8)0.95440.0456显然，它也是测量列中单次测量值的测量0.99730.0027极限误差。0.999360.00064选择不同的t值，就对应不同的概率测量极限误差的可信程度也就不一样。随机误差在+to范围内出现的概率称为置信概率，t称为置信因子或置信系数。在几何量测量中，通常取t-3，即置信概率为99.73%。2.测量列中随机误差的处理步骤①计算测量列中各个测得值的算术平均值F-2设测量列测得值为x1、x2、、x，则算术平均值为(2-9)②计算残差用算术平均值代替真值后，计算残余误差（简称残差），记为vi，即=x-x(2-10)残差具有两个特性：残差的代数和等于零。可用来校核及其残差计算的正确性残差的平方和为最小。用作为测量结果最可靠且最合理。③估算测量列中单次测量值的标准偏差接贝癌 (）公式计算由单次葡量重值的标准病差的估计值后(2-11)这时，单次测量值的测量结果x可表示为x=x,±30(2-12) ④计算测量列算术平均值的标准偏差若相同测量条件对同一被测量进行多组测量（每组皆测量N次），则每组测量的算术平均值可能不相同。但其分散程度要比单次测量值的分散程度小得多。说明测量次数越多，就越小，测量精密度就越高。但当一定时，N>10以后，减小已很缓慢，故一般取N=10～15次为宜。85各类测量误差的处理根据误差理论，测量列算术平均值的标准偏差与测量列单次测量值的标准偏差存在如下i关系：(2-13)

10 而测量次数一般不超过几十次，随机误差 超出±3σ的情况实际上很难出现。因此，可 取 δ=±3σ作为随机误差的极限值，记 (2-8) 显然，它也是测量列中单次测量值的测量 极限误差。 选择不同的 t 值，就对应不同的概率， 测量极限误差的可信程度也就不一样。随机 误差在±tσ范围内出现的概率称为置信概率，t 称为置信因子或置信系数。在几何量测量中， 通常取 t=3，即置信概率为 99.73%。 2. 测量列中随机误差的处理步骤 ① 计算测量列中各个测得值的算术平均值 设测量列测得值为 x1、x2、.、xN，则算术平均值为 (2-9) ②计算残差 用算术平均值代替真值后，计算残余误差（简称残差），记为 νi，即 (2-10) 残差具有两个特性： 残差的代数和等于零。可用来校核 及其残差计算的正确性。 残差的平方和为最小。用 作为测量结果最可靠且最合理。 ③ 估算测量列中单次测量值的标准偏差 按贝塞尔（Bessel）公式计算出单次测量值的标准偏差的估计值。 (2-11) 这时，单次测量值的测量结果 xe可表示为 (2-12) ④ 计算测量列算术平均值的标准偏差 若相同测量条件对同一被测量进行多组测量（每组皆测量 N 次），则每组测量的算术平均 值可能不相同。但其分散程度要比单次测量值的分散程度小得多。 说明测量次数越多,就越小，测量精密度就越高。但当一定时，N>10 以后，减小已很缓慢， 故一般取 N=10～15 次为宜。 §5 各类测量误差的处理 根据误差理论，测量列算术平均值的标准偏差与测量列单次测量值的标准偏差存在如下 关系： (2-13) t 不超出的概率 超出的概率 1 2 3 4 1 2 3 4 0.6826 0.9544 0.9973 0.99936 0.3174 0.0456 0.0027 0.00064  lim = 3 = = N i i x N x 1 1 v x x i = i − 1 1 1 2 − = = N i i v N  xe = xi 3 N σ σ x =