南京大学：《非线性物理学》课程电子教案（课件讲稿）非线性物理混沌物理1/4（负责人：刘俊明）

非线性物理：混沌物理 形态多样性：以平方映射为例 。 最简单动力学系统可以表示为(4为控制参数)： y=(4,x) xn=f(u,xn) 1838年，生物学家Verhulst在研究生物种群演化时提出平方映 射演化方程，也即logistic map: x1-x) 数学物理学家R.May于1971年发现了这一单参量方程竞然具有 不同寻常的行为。微分形式（与迭代方程稍有不同）： dx =x(1-x) dt

非线性物理：混沌物理 形态多样性：以平方映射为例 • 最简单动力学系统可以表示为(  为控制参数)： yf x  (,)  • 1838年，生物学家 Verhulst 在研究生物种群演化时提出平方映 射演化方程，也即logistic map： ( , ) n 1 n x  f  x  (1 ) n 1 n n x  x  x   • 数学物理学家 R. May 于1971年发现了这一单参量方程竟然具有 不同寻常的行为。 微分形式(与迭代方程稍有不同)： x(1 x) dt dx   

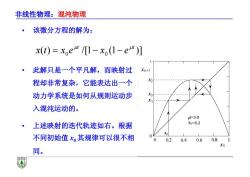
非线性物理：混沌物理 该微分方程的解为： x(t)=xe“/1-x(1-e“)] 此解只是一个平凡解，而映射过 Xn+1 程却非常复杂，它能表达出一个 动力学系统是如何从规则运动步 入混沌运动的。 4=3.0 ·上述映射的迭代轨迹如右。根据 x0=0.2 不同初始值x其规律可以很不相 0 0 0.20.4 0.608 Xn 同

非线性物理：混沌物理 • 该微分方程的解为： • 此解只是一个平凡解，而映射过 程却非常复杂，它能表达出一个 动力学系统是如何从规则运动步 入混沌运动的。 • 上述映射的迭代轨迹如右。根据 不同初始值 x0 其规律可以很不相 同。 ( ) /[1 (1 )] 0 0 t t x t x e x e     

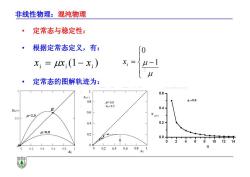
非线性物理：混沌物理 ·定常态与稳定性： 根据定常态定义，有： 0 x:=X(1-x) 定常态的图解轨迹为： 0.6 Xn+1 μ0.8 =0.8 0=0.5 Xn+ B 0.6 0.5 l-2.5 0.4 0.2 1=0.8 0.2 0.0 02 0406 0.8 0020.40.6081 n

非线性物理：混沌物理 • 定常态与稳定性： • 根据定常态定义，有： • 定常态的图解轨迹为： xxx iii   ( ) 1     1 0 i x

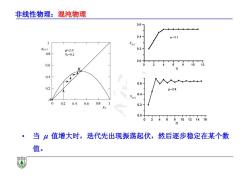
非线性物理：混沌物理 06 ◆◆◆◆◆◆ 0.4 μ=2.1 Xn+l Xn+1 1=2.0 0.2 08 0=0.2 0.0 0.6 0.4 0.6 0.2 1=2.8 0.4 A 0 0.20.4 0.60.8 02 Xn 0.0 0 46810121416 当山值增大时，迭代先出现振荡起伏，然后逐步稳定在某个数 值

非线性物理：混沌物理 • 当  值增大时，迭代先出现振荡起伏，然后逐步稳定在某个数 值

非线性物理：混沌物理 在定常态附近进行稳定性分析： x=f(uxn) x*=f(山，*) 在定常态x*处施加微扰6，则： x *+n=f(Lx*+n) x*+61=fu,x*）+4 8x x=x of(u,x) En 8x x=Y* 稳定不动点应该满足： Entl En m=≤1

非线性物理：混沌物理 • 在定常态附近进行稳定性分析： • 在定常态 x* 处施加微扰 n，则： ( , ) n 1 n x  f  x  x*  f (, x*) * ( , * ) n 1 n x   f  x           n x x n x f x x f x     * 1 ( , ) * ( , *) * 1 ( , ) n x x n x f x m          • 稳定不动点应该满足：   n+1 n  m  1

非线性物理：混沌物理 01表示迭代指数增长发散。 -1<0:迭代经过几次上下起伏趋近于x*,<-1表示迭代指数 振荡增长发散。 周期解： 按照上述稳定性分析，从初值x出发，迭代过程要么发散，要么 收敛到两个定常态之一。然而，在合适的μ值情况下，迭代过程 表现为：xf小，xf,循环往复，出现倍周期解。 周期2解应该满足：x=ffx)》→f2x),周期4解满足 x=f0f0f0f》→f4)

非线性物理：混沌物理 • 01表示迭代指数增长发散。 • -1<m<0：迭代经过几次上下起伏趋近于 x*， m<-1表示迭代指数 振荡增长发散。 • 周期解： • 按照上述稳定性分析，从初值 x0 出发，迭代过程要么发散，要么 收敛到两个定常态之一。然而，在合适的  值情况下，迭代过程 表现为：x2=f(x1)，x1=f(x2)，循环往复，出现倍周期解。 • 周期2解应该满足：x=f(f(x)) f 2(x)，周期4解满足 x=f(f(f(f(x)))) f 4(x)

非线性物理：混沌物理 以x=f2x为例，方程变为： x=f(f(x》=4I(1-x][1-(1-x)] x-4[x(1-x][1-x(1-x]=O ·方程x=fx的两个定常解依然是上述方程的两个根，从而求得另 外两个根： -〔--++u--0 ,=(+1)生u+1u-3 24

非线性物理：混沌物理 • 以 x=f 2 (x)为例，方程变为： • 方程 x=f (x)的两个定常解依然是上述方程的两个根，从而求得另 外两个根：

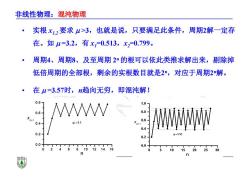
非线性物理：混沌物理 实根x2要求4>3，也就是说，只要满足此条件，周期2解一定存 在。如μ=3.2，有x=0.513,x2=0.799。 ·周期4、周期8、及至周期2"的根可以依此类推求解出来，剔除掉 低倍周期的全部根，剩余的实根数目就是2“，对应于周期2解。 ·在μ=3.57时，n趋向无穷，即混沌解！ 0.8 0.6 V 08 0.4 μ=3.1 型 0.4 0.2 =3.S2 0.2 6 0.0 10 15202530

非线性物理：混沌物理 • 实根 x1,2要求  >3，也就是说，只要满足此条件，周期2解一定存 在。如  =3.2，有 x1=0.513，x2=0.799。 • 周期4、周期8、及至周期 2n 的根可以依此类推求解出来，剔除掉 低倍周期的全部根，剩余的实根数目就是2n，对应于周期2n解。 • 在  =3.57时，n趋向无穷，即混沌解！

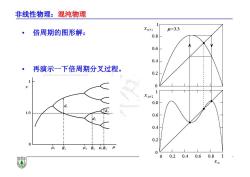
非线性物理：混沌物理 倍周期的图形解： Xn+l =3.3 0.8 0.6 0.4 再演示一下倍周期分叉过程。 0.2 0 Xn+2 0.8 1/2 d3 0.6 0.4 0.2 4R M:RR 00.20.40.60.81 福 Xn

非线性物理：混沌物理 • 倍周期的图形解： • 再演示一下倍周期分叉过程

非线性物理：混沌物理 驱动与耗散的竞争： ·从物理本质上看，分岔是非线性系统驱动力和耗散力竞争达到临 界状态而对应的演化行为转变。再以平方映射为例： Xn1=Ln (1-xn) 显然，心n是驱动力，心是耗散力，两者之间竞争导致状态的 丰富多样。在定常态附近判断两力相对大小依赖于： 6xn+1 of x=x*

非线性物理：混沌物理 驱动与耗散的竞争： • 从物理本质上看，分岔是非线性系统驱动力和耗散力竞争达到临 界状态而对应的演化行为转变。再以平方映射为例： (1 ) n 1 n n x  x  x   • 显然，xn是驱动力，-xn2是耗散力，两者之间竞争导致状态的 丰富多样。在定常态附近判断两力相对大小依赖于：