吉林大学：《线性代数》课程教学资源（PPT课件）第一章 行列式 08-1-4 §4 克拉默法则

例1.解方程组 2x1+x2-5x3+x4=8 x1-3x2 -6x4=9 2x2-X3+2x4=-5 解： x1+4x2-7x3+6x4=0 2 -5 0 -5 13 5 13 -3 6 -3 6 2 -1 -1 2 0 2 2 2 1 -7 6 7 12 3 27 7 -2

例1.解方程组        + − + = − + = − − − = + − + = 4 7 6 0 2 2 5 3 6 9 2 5 8 1 2 3 4 2 3 4 1 2 4 1 2 3 4 x x x x x x x x x x x x x x 解: 1 4 7 6 0 2 1 2 1 3 0 6 2 1 5 1 − − − − − D = 0 7 7 12 0 2 1 2 1 3 0 6 0 7 5 13 − − − − − = 7 7 12 2 1 2 7 5 13 − − − = − 7 7 2 0 1 0 3 5 3 − − − − − − = − 27. 7 2 3 3 = − − − =

1-5 8 1 2 -5 -3 0 -6 D =81 D2 =-108 -5 2 -1 2 0 -5 0 4 -7 6 0 -7 2 8 1 2 -5 8 -3 -6 1 -3 D =-27D4= =27 0 2 -5 2 0 2 4 -7 0

81 0 4 7 6 5 2 1 2 9 3 0 6 8 1 5 1 1 = − − − − − − D = 108 1 0 7 6 0 5 1 2 1 9 0 6 2 8 5 1 2 = − − − − − − D = 27 1 4 0 6 0 2 5 2 1 3 9 6 2 1 8 1 3 = − − − − D = 27 1 4 7 0 0 2 1 5 1 3 0 9 2 1 5 8 4 = − − − − − D =

x1=3 于是得原方程组的解为 2=4 x3=-1 x4=1 定理2.如果线性方程组(1)的系数行列式D不等于Q, 则(1)有唯一的解 定理2'如果线性方程组(1)无解或有多个解，则它的 系数行列式必为0

定理2.如果线性方程组（1）的系数行列式D不等于0, 则(1)有唯一的解. 定理 .如果线性方程组(1)无解或有多个解，则它的 系数行列式必为0. 于是得原方程组的解为        = = − = − = 1 1 4 3 4 3 2 1 x x x x 2

二齐次线性方程组的克拉默法则 设齐次线性方程组 a1x1+a42X2++a1nxm三0 a21x1+a22X2+…+a2mxm= 0 amx+an2x2++amnxn=O 若(4)的系数行列式 d12 azi d22 n2 nn 则(4)没有非零解

二.齐次线性方程组的克拉默法则 设齐次线性方程组        + + + = + + + = + + + = 0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 n n n n n n n n n a x a x a x a x a x a x a x a x a x     (4) 若(4)的系数行列式 0 1 2 2 1 2 2 2 1 1 1 2 1 =  n n n n n n a a a a a a a a a D       (5) 则(4)没有非零解

定理3.如果齐次线性方程组(4) 的系数行列式D不等于0，则齐次线性 方程组(4)没有非零解 定理3'如果齐次线性方程组(4) 有非零解，则它的系数行列式必为0。 例2.问几在什么条件下，方程组 2x1+x2=0 x1+2x2=0 有非零解？

. 定理 .如果齐次线性方程组(4) 有非零解,则它的系数行列式必为0。 定理3.如果齐次线性方程组(4) 的系数行列式D不等于0,则齐次线性 方程组(4)没有非零解. 例2. 问  在什么条件下,方程组    + = + = 0 0 1 2 1 2 x x x x   有非零解？ 3

解：由定理3知，若方程组 有非零解，则其系数行列式必为零。 D=径=0一”2 入=122=-1 所以，当人=-1或入=1时，上面方程组有非 零解

解：由定理 知，若方程组 有非零解，则其系数行列式必为零。 所以，当 或 时，上面方程组有非 零解。  = −1  =1 1, 1 0 1 0 1 1 1 2 2 = = − = =  − =      D 3

例3设非齐次线性方程组 几x1+x2+x3=1 x1+入x2+x3=入 x1+x2+2x3=2 问)为何值时，该方程组有唯一解，并求其解。 解：方程组的系数行列式为 =a+2a- 显然当2≠一2，入≠1时，方程组有唯一解

例3 设非齐次线性方程组 1 2 3 1 2 3 2 1 2 3 x x x 1 x x x x x x       + + =   + + =   + + = 问λ 为何值时，该方程组有唯一解，并求其解。 解：方程组的系数行列式为 1 1 1 1 1 1    =（λ +2） 2 ( 1)  − 显然当λ ≠－2，λ ≠ 1时，方程组有唯一解。 D=

=-(2-1)2(2+1 22 1 1 1 1 =(2-1D月 22 21 1 1 =(2+1)2(2-1) 1 2

1 2 1 1 1 1 1 D     = 2 = − − + ( 1) ( 1)   2 2 1 1 1 1 1 D     = = 2 ( 1)  − 3 2 1 1 1 1 1 D     = = 2 2 ( 1) ( 1)   + −

(2-1)(2+1) 见+1 X1三 D (2-1)2(2+2 +2 D, (2-1)2 X2月 D (2-1)2(2+2 2+2 、 3(2-1)2(2+12 (2+1)2 D (2-1)2(2+2 2+2

1 1 D x D = = 1 2   + − + 2 2 D x D = = 2 2 ( 1) ( 1) ( 2)    − = − + 1  + 2 2 2 2 ( 1) ( 1) ( 1) ( 2)     − + = − + 2 ( 1) 2   + + 3 3 D x D = = 2 2 ( 1) ( 1) ( 1) ( 2)     − + − = − +

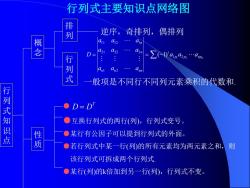
行列式主要知识点网络图 列 逆序，奇排列，偶排列 an a12 念 D= a21 22 d .:: .: 列式 an2 a 般项是不同行不同列元素乘积的代数和 行列式知识点 D=D ●互换行列式的两行（列，行列式变号。 ●某行有公因子可以提到行列式的外面。 质 ●若行列式中某一行（列的所有元素均为两元素之和， 则 该行列式可拆成两个行列式 。某行（列的k倍加到另一行（列，行列式不变

行列式主要知识点网络图 概 念 排 列 行 列 式 逆序，奇排列，偶排列 一般项是不同行不同列元素乘积的代数和. ● ●互换行列式的两行(列)，行列式变号。 ●某行有公因子可以提到行列式的外面。 ●若行列式中某一行(列)的所有元素均为两元素之和，则 该行列式可拆成两个行列式. ●某行(列)的k倍加到另一行(列)，行列式不变。 T D = D 行 列 式 知 识 点 性 质 = =  − n p p n p t n n n n n n a a a a a a a a a a a a D        1 2 1 2 1 2 2 1 2 2 2 1 1 1 2 1 ( 1)