吉林大学：《线性代数》课程教学资源（PPT课件）第二章 矩阵及其运算 17-2-4 §4 分块矩阵

第八讲 §4.分块矩阵 一、分块矩阵的定义 把一个阶数较高的矩阵，用若干条横线和竖线分成 若干小块，每一小块都叫做矩阵的子块，以子块为元素 的矩阵称为分块矩阵

§4.分块矩阵 第 八 讲 一、分块矩阵的定义 把一个阶数较高的矩阵,用若干条横线和竖线分成 若干小块 , 每一小块都叫做矩阵的子块 ,以子块为元素 的矩阵称为分块矩阵

例如：将3×4矩阵 2 03 4 A=21 022 23 Q24 31 032 33 034 分块形式如下：

例如：将3×4矩阵           = 3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 4 a a a a a a a a a a a a A 分块形式如下：

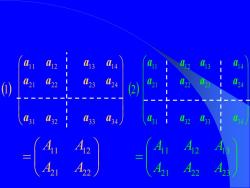
3 00 03 022 03 2 04 032 An A2 A

        = 21 22 23 11 12 13 A A A A A A ( )               3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 4 1 a a a a a a a a a a a a ( )               3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 4 2 a a a a a a a a a a a a 11 12 21 22 A A A A   =    

3) 431 032 A2 A13 012 13 L14 21 0L22 0123 24 31 32 033 034

( ) = A11 A12 A13 A14           = 31 21 11 A A A ( )           3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 3 3 a a a a a a a a a a a a ( )                 3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 4 4 a a a a a a a a a a a a

二、分块矩阵的运算 1、分块矩阵的加法： 同型矩阵，分法相同，对应 子块相加 设A和B均为mXn矩阵，分法下： B A

          = s s r r A A A A A     1 1 1 1           = s s r r B B B B B     1 1 1 1 二、分块矩阵的运算 1、分块矩阵的加法： 同型矩阵,分法相同,对应 子块相加. 设 A 和 B 均为 m×n矩阵,分法下:

其中A与B的行数相同，列数 相同，那末 A+B1·A,+B A+B A1+B1· Asr+B 其运算律与矩阵的加法相同

相同 那末 其中 与 的行数相同 列数 , , Ai j Bi j           + + + + + = s s s r s r r r A B A B A B A B A B     1 1 1 1 1 1 1 1 其运算律与矩阵的加法相同

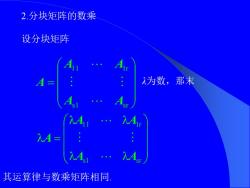
2.分块矩阵的数乘 设分块矩阵 A 2为数，那末 入A 入A 入A= 其运算律与数乘矩阵相同

2.分块矩阵的数乘 设分块矩阵           = s 1 s r 11 1r A A A A A     λ为数，那末                = s1 s r 1 1 1r A A A A A     其运算律与数乘矩阵相同

3.分块矩阵的乘法 设A为mXI矩阵，B为 1Xn矩阵，分块成 A12 A=

3.分块矩阵的乘法. 设A为 m×l 矩阵，B为 l×n矩阵，分块成                 = t 1 t j t r i 1 i j i r 1 1 1j 1 r B B B B B B B B B B                                 = s t A A A A A A A A A A s            1 s 2 i 1 i 2 i t 1 1 1 2 1t

其中A1,A2,…,A列数分别等于 B,B,…,B的行数，那末 AB 其中 C=AB,+A2B2,+…+A,B (i=1,2,…,S7=1,2,…,r）

其中Ai1 , Ai 2,  , Ai t列数分别等于               = s 1 s 2 s r 2 1 2 2 2r 1 1 1 2 1r C C C C C C C C C AB        那末 其中 Ci j = Ai1 B1 j + Ai2 B2 j ++ Ai tBt j ( 1,2, , ; 1,2, , ) i s j r = = 1j 2j tj B B B , , , 的行数