吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 24-3-2 §2 矩阵的秩

因此D≠0,从而R(B)≥ ri+kri 当AB,分三种情况讨论: ①D中不含有第行; ②D,中同时含有第行和第j行; ③D中含有第行,但不含有第j行 对①和②两种情况,显然B中与D对应的子 式D,=D≠0,故R(B)≥r:
因此 Dr 0 ,从而R(B)≥r 当 ,分三种情况讨论: ①Dr中不含有第 i行; ②Dr中同时含有第 i行和第 j 行; ③Dr中含有第 i行,但不含有第 j 行. 对①和 ②两种情况,显然B 中与Dr对应的子 式 Dr = Dr 0 ,故R(B)≥r; ~ i j r kr A B +

对于③,由 历- +kr,=D,+kD. 若D≠0,则因D, 中不含有第行,可知A中 有不含第行的r非零子式,从而R(B)≥r;若 D,=0,则D=D≠0,故也有R(B)≥r
对于③,由 r i j i j Dr kDr D = r + k r = r + k r = + 若 0 , Dr Dr = 0 则因 Dr 中不含有第 i行,可知A中 有不含第 i行的r阶非零子式,从而R(B)≥r;若 ,则Dr = Dr 0 ,故也有R(B)≥r

以上证明了若A经过一次初等行变换为B,则 R(A)≤R(B),由于B亦可经过一次初等行变换 变为A.故也有R(B)≤R(A),因此R(A) R(B) 经过一次初等行变换矩阵的秩不变,故经过有限次 初等行变换时,矩阵的秩依然不变。 同理可证:A经过有限次初等列变换,变成矩阵B, 则有R(A)=R(B). 总之,若A经过有限次初等变换变为矩阵B,则有 R(A)=R(B)
以上证明了若A经过一次初等行变换为B, 则 R(A)≤R(B),由于B亦可经过一次初等行变换 变为A.故也有R(B)≤R(A).因此R(A)= R(B)。 经过一次初等行变换矩阵的秩不变,故经过有限次 初等行变换时,矩阵的秩依然不变。 同理可证:A经过有限次初等列变换,变成矩阵B, 则有 R(A)=R(B). 总之,若A经过有限次初等变换变为矩阵B,则有 R(A)=R(B).

如在例1中,我们已经计算 023 的秩为2,将A施行初等变换得 显然,R(B)=2,故RA)=R(B) 通过上面定理的证明和上面秩的计算,以后求矩阵的 秩,只需将矩阵用初等变换变成阶梯形矩阵即可
如在例1中,我们已经计算 的秩为2,将A施行初等变换得 1 2 3 0 1 11 0 1 11 A − − − − 1 2 3 0 1 11 0 0 0 B − − = 显然,R(B) = 2 , 故 R(A) = R(B) 。 通过上面定理的证明和上面秩的计算,以后求矩阵的 秩,只需将矩阵用初等变换变成阶梯形矩阵即可。 1 2 3 2 3 5 4 7 1 = − A

三、求秩。 ●例2设 73 2 0 5 3 -2 3 A= 2 求矩阵A的秩.并求A的一个最高阶的非零子式
三、求秩. ⚫ 例2 设 − − − − − = 1 6 4 1 4 2 0 1 5 3 3 2 3 6 1 3 2 0 5 0 A 求矩阵A的秩.并求A的一个最高阶的非零子式
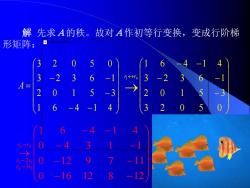
解先求A的秩。故对A作初等行变换,变成行阶梯 形矩阵:回 2 3 -2 3 2 2 3 2 12 -3 -16
解 先求A的秩。故对A作初等行变换,变成行阶梯 形矩阵: − − − − − = 1 6 4 1 4 2 0 1 5 3 3 2 3 6 1 3 2 0 5 0 A − − − − − → 3 2 0 5 0 2 0 1 5 3 3 2 3 6 1 1 6 4 1 4 1 4 r r − − − − − − − − → − − − 0 16 12 8 12 0 12 9 7 11 0 4 3 1 1 1 6 4 1 4 2 4 4 1 3 1 3 2 r r r r r r

-12 -16 r4- -8 -8 因为阶梯形矩阵有3个非零行,所以R(B)=3。从而 RA)=3
− − − − − − − − → − − − 0 16 12 8 12 0 12 9 7 11 0 4 3 1 1 1 6 4 1 4 2 4 4 1 3 1 3 2 r r r r r r − − − − − → − 0 0 0 0 0 0 0 0 4 8 0 4 3 1 1 1 6 4 1 4 4 3 r r 因为阶梯形矩阵有3个非零行,所以 R(B) = 3。从而 R(A) = 3。 3 2 4 2 3 4 1 6 4 1 4 0 4 3 1 1 0 0 0 4 8 0 0 0 4 8 r r r r − − − − − − − − →

A的一个最高阶非零子式为: 3 2 32 6 3 -26=6 0 11 =-2 2 2 5 2 设A为阶可逆矩阵,则A0,从而R(A)=n,称4为满 秩矩阵。 若A为n阶不可逆矩阵,则A=0,从而R(A)大n,称A为 降秩矩阵
A的一个最高阶非零子式为: 0 2 5 6 11 2 2 0 5 6 0 11 3 2 5 2 0 5 3 2 6 3 2 5 − = = − 设A为n阶可逆矩阵,则|A|≠0,从而R(A) = n,称A为满 秩矩阵。 若A为n阶不可逆矩阵,则|A|=0,从而R(A)< n,称A为 降秩矩阵

例3设 2 -4 8 0 A -2 b 4 -2 3 23 6 6 求矩阵A及矩阵B=(A|b)的秩
例3 设 − − − − − − − = 3 6 0 6 2 4 2 3 2 4 8 0 1 2 2 1 A = 4 3 2 1 b 求矩阵A及矩阵B=(A | b)的秩

解 -2 2 - -22 -1 3-21 2 -4 8 2 5+2 B -2 3 3 -3 3 -6 3÷5 0 4+3r -13 因此,R(A)=2,R(B)=3
解 − − − − − − − = 3 6 0 6 4 2 4 2 3 3 2 4 8 0 2 1 2 2 1 1 B − − → − + 0 0 0 0 1 0 0 0 0 5 0 0 2 1 0 1 2 2 1 1 3 2 2 4 2 2 3 r r r r r − − → − 0 0 0 0 0 0 0 0 0 1 0 0 2 1 0 1 2 2 1 1 3 5 4 3 r r r 因此,R(A) = 2 , R(B) = 3. 2 1 3 1 4 1 2 2 3 1 2 2 1 1 0 0 4 2 0 0 0 2 1 5 0 0 6 3 1 r r r r r r − + − − − − − →
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 23-3-2 §2 矩阵的秩.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 22-3-1 §1 矩阵的初等变换.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 21-3-1 §1 矩阵的初等变换.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 20-2-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 19-2-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 18-2-4 §4 分块矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 17-2-4 §4 分块矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 16-2-3 §3 逆矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 15-2-3 §3 逆矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 14-2-2 §2 矩阵的运算.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 13-2-2 §2.矩阵的运算.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 12-2-1 §2.矩阵的运算.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 11-2-1 §1.矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 10-1-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 09-1-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 08-1-4 §4 克拉默法则.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 07-1-4 §4 克拉默法则.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 06-1-3 §3 行列式按行(列)展开.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 05-1-3 §3 行列式按行(列)展开.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 04-1-2 §2 行列式的性质.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 25-3-3 §3 线性方程组的解.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 26-3-3 §3 线性方程组的解.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 27-3-4 §4 初等矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 28-3-4 §4 初等矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 29-3-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 30-3-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 31-4-1-2 §1 n维向量.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 32-4-1-2 §2 向量组的线性相关性.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 33-4-2-3 §2 向量组的线性相关性.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 34-4-3 §3 线性相关性的判定.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 35-4-4 §4 向量组的秩.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 36-4-4 §4 向量组的秩.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 37-4-5 §5 向量空间.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 38-4-5 §5 向量空间.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 41-4-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 42-4-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 43-5-1 §1 向量的内积.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 44-5-1 §1 向量的内积.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 45-5-2 §2 方阵的特征值与特征向量.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 46-5-2 §2 方阵的特征值与特征向量.ppt
