吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 26-3-3 §3 线性方程组的解
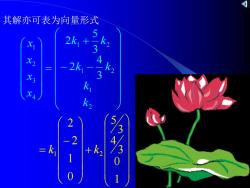
其解亦可表为向量形式 2k1+ 2k2 2k 2 -2 1
其解亦可表为向量形式 − − + = 2 1 1 2 1 2 4 3 2 1 3 4 2 3 5 2 k k k k k k x x x x + − = 1 0 3 4 3 5 0 1 2 2 1 2 k k

例2求解非齐次线性方组 x1-2x2+3x3-x4=1 3x1-x2+5x3-3x4=2 2x1+x2+2x3-2x4=3 解对增广矩阵B实施行的初等变换 023100-23 B= 3-15-32~05 0-1 212-2305 -40
例2 求解非齐次线性方组 + + − = − + − = − + − = 2 2 2 3 3 5 3 2 2 3 1 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x 解 对增广矩阵B实施行的初等变换 − − − − − = 2 1 2 2 3 3 1 5 3 2 1 2 3 1 1 B 1 2 3 1 1 ~ 0 5 4 0 1 0 5 4 0 1 − − − − −

71 -2 3 5 0 可见,R(A)=2,R(B)=3.故方程组无解
− − − − 0 0 0 0 2 0 5 4 0 1 1 2 3 1 1 ~ 可见,R(A) = 2 , R(B) =3.故方程组无解

例3 求解非其次线性方程组 x1+x2一3x3-x4三1 3x1-x2-3x3+4x4= 4 x1+5x2一9x3-8x4=0 解对增广矩阵B实施行的初等变换 B=3-1 15-9-8 004-6-7 -1
例3 求解非其次线性方程组 + − − = − − + = + − − = 5 9 8 0 3 3 4 4 3 1 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x 解 对增广矩阵B实施行的初等变换 − − − − − − = 1 5 9 8 0 3 1 3 4 4 1 1 3 1 1 B − − − − − − 0 4 6 7 1 0 4 6 7 1 1 1 3 1 1 ~

-4 7 0 显然,R(4)=R(B)=2<4,所以原方程组有无穷多解, 且具有下列同解方程组:
− − − 0 0 0 0 0 0 4 6 7 1 1 1 3 1 1 ~ − − − 0 0 0 0 0 0 4 6 7 1 4 4 12 4 4 ~ − − 0 0 0 0 0 0 4 6 7 1 4 0 6 3 5 ~ − − − − 0 0 0 0 0 4 1 4 7 2 3 0 1 4 5 4 3 2 3 1 0 ~ 显然, R(A) = R(B) = 2<4,所以原方程组有无穷多解, 且具有下列同解方程组:

3 3-232 即 23 2 3-2 3 1 故 X2 2 k1,为任意常数。 k K2
− − = − − + = 4 1 4 7 2 3 4 5 4 3 2 3 2 3 4 1 3 4 x x x x x x 即 = + − = − + 4 1 4 7 2 3 4 5 4 3 2 3 2 3 4 1 3 4 x x x x x x 故 k1 , k2 为任意常数。 1 1 2 2 1 2 3 1 4 2 3 3 5 2 4 4 3 7 1 2 4 4 x k k x k k x k x k = − + = + − = =

写成向量形式 32 3 休 k1,k2为任意常数
1 2 1 2 1 2 3 1 4 2 3 3 5 2 4 4 3 7 1 2 4 4 k k x x k k x k x k − + = + − − + − + = 0 0 4 1 4 5 1 0 4 7 4 3 0 1 2 3 2 3 k1 k2 k1 ,k2 为任意常数。 写成向量形式

例4设有线性方程组 (1+九)x1+x2+x3=0 x1+(1+)x2+x3=3 x1+x2+(1+入)x3=见 问λ取何值时,此方程组(1)有唯一解?(2)无解? (3)有无穷多个解?并在有无穷多解时,求其通解
例4 设有线性方程组 问 λ 取何值时,此方程组(1)有唯一解?(2)无解? (3)有无穷多个解?并在有无穷多解时,求其通解。 + + + = + + + = + + + = 1 2 3 1 2 3 1 2 3 (1 ) (1 ) 3 (1 ) 0 x x x x x x x x x

解对增广矩阵B=(A|b)实施 行的初等变换: +入 1+入 3 1 1+九入 1+见 1+ 3 1+入
解 对增广矩阵B =(A | b)实施 行的初等变换: + + + = 1 1 1 1 1 1 3 1 1 1 0 B + + + 1 1 1 0 1 1 1 3 1 1 1 ~

11+2元 3 1+ 0 1+元 -2 3-入 0 -(2+2)-21+2) 1+见 兄 -见 3-见 -(3+2) (3+2)1-2)
+ + + 1 1 1 0 1 1 1 3 1 1 1 ~ − − + − + − − + 0 (2 ) (1 ) 0 3 1 1 1 ~ − + + − − − + 0 0 (3 ) (3 )(1 ) 0 3 1 1 1 ~
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 25-3-3 §3 线性方程组的解.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 24-3-2 §2 矩阵的秩.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 23-3-2 §2 矩阵的秩.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 22-3-1 §1 矩阵的初等变换.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 21-3-1 §1 矩阵的初等变换.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 20-2-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 19-2-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 18-2-4 §4 分块矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 17-2-4 §4 分块矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 16-2-3 §3 逆矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 15-2-3 §3 逆矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 14-2-2 §2 矩阵的运算.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 13-2-2 §2.矩阵的运算.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 12-2-1 §2.矩阵的运算.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第二章 矩阵及其运算 11-2-1 §1.矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 10-1-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 09-1-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 08-1-4 §4 克拉默法则.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 07-1-4 §4 克拉默法则.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第一章 行列式 06-1-3 §3 行列式按行(列)展开.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 27-3-4 §4 初等矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 28-3-4 §4 初等矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 29-3-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第三章 矩阵的初等变换与线性方程组 30-3-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 31-4-1-2 §1 n维向量.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 32-4-1-2 §2 向量组的线性相关性.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 33-4-2-3 §2 向量组的线性相关性.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 34-4-3 §3 线性相关性的判定.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 35-4-4 §4 向量组的秩.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 36-4-4 §4 向量组的秩.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 37-4-5 §5 向量空间.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 38-4-5 §5 向量空间.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 41-4-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第四章 向量组的线性相关性 42-4-习题课.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 43-5-1 §1 向量的内积.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 44-5-1 §1 向量的内积.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 45-5-2 §2 方阵的特征值与特征向量.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 46-5-2 §2 方阵的特征值与特征向量.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 47-5-3 §3 相似矩阵.ppt
- 吉林大学:《线性代数》课程教学资源(PPT课件)第五章 相似矩阵及二次型 48-5-3 §3 相似矩阵.ppt
