《概率论与数理统计》课程教学资源(PPT课件)第七章 参数估计(习题课)

概率伦与款理统外 第七章 参数估计 习题课 一、重点与难点 二、主要内容 三、典型例题
第七章 参数估计 习 题 课 一、重点与难点 三、典型例题 二、主要内容

概车纶与款理统外 一、重点与难点 1.重点 最大似然估计. 一个正态总体参数的区间估计. 2.难点 显著性水平与置信区间
一、重点与难点 1.重点 最大似然估计. 一个正态总体参数的区间估计. 2.难点 显著性水平 与置信区间
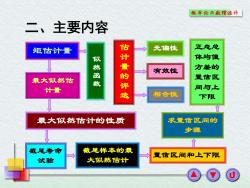
概率伦与款理统外 二、主要内容 矩估计量 无偏性 正态总 体均值 似然函教 估计量的评选 有效性 方差的 最大以然估 置信区 计量 间与上 相合性 下限 最大以然估计的性质 求置信区间的 步骤 戴尾寿命 载尾样本的最 置信区间和上下限 试验 大似然估计
矩估计量 估 计 量 的 评 选 截尾样本的最 大似然估计 截尾寿命 试验 二、主要内容 最大似然估 计量 最大似然估计的性质 似 然 函 数 无偏性 正态总 体均值 方差的 置信区 间与上 下限 有效性 置信区间和上下限 求置信区间的 步骤 相合性

概车纶与款理统外 矩估计量 用样本矩来估计总体矩,用样本矩的连续 函数来估计总体矩的连续函数,这种估计法称 为矩估计法. 矩估计法的具体做法:令山=A1,1=1,2,k, 这是一个包含k个未知参数日,日2,.,0的方程组, 解出其中0,02,.,0g 用方程组的解0,0,.,0分别作为0,02,.,0的 估计量,这个估计量称为矩估计量
矩估计量 用样本矩来估计总体矩,用样本矩的连续 函数来估计总体矩的连续函数,这种估计法称 为矩估计法. 矩估计法的具体做法: A , l 1, 2, ,k , 令 l = l = , , , , 这是一个包含 k 个未知参数1 2 k 的方程组 , , , . 解出其中1 2 k , . , , , ˆ , , ˆ , ˆ 1 2 1 2 估计量 这个估计量称为矩估计量 用方程组的解 k 分别作为 k 的

概華论与款醒硫外 最大似然估计量 得到样本值x1,x2,xn时,选取使似然函数L() 取得最大值的0作为未知参数0的估计值, 即L(x1,x2,.,xn;0)=maxL(x1,x2,xn;) (其中®是O可能的取值范围) 这样得到的0与样本值x1,x2,xn有关,记为 (x1,x2,.,xn),参数0的最大似然估计值 (X1,X2,.,X)参数0的最大似然估计量
最大似然估计量 , , , , ( ) 得到样本值 x1 x2 xn 时 选取使似然函数 L , 取得最大值的 ˆ 作为未知参数 的估计值 ) max ( , , , ; ). ˆ ( , , , ; 1 2 1 2 L x x xn L x x xn 即 = (其中 是 可能的取值范围) ( , , , ), ˆ , , , , ˆ 1 2 1 2 n n x x x x x x 这样得到的 与样本值 有关 记为 ( , , , ) ˆ X1 X2 Xn 参数 的最大似然估计值, 参数 的最大似然估计量

概车纶与款理统外 最大似然估计的性质 设0的函数u=u(0),0∈⊙具有单值反函 数0=0(uW),u∈U,又设0是X的概率密度函数 f(x;)(f形式已知)中的参数0的最大似然估 计,则i=u()是u(0)的最大似然估计
最大似然估计的性质 ) ( ) . ˆ , ˆ ( ( ; ) ( ) ˆ ( ), , ( ), 计 则 是 的最大似然估计 形式已知 中的参数 的最大似然估 数 又设 是 的概率密度函数 设 的函数 具有单值反函 u u u f x f u u U X u u = = =

概華论与款醒硫外 似然函数 1.设总体X属离散型 L()=L(x,x2,xi0)=Πp(xi0),0∈® i=1 L(O)称为样本似然函数 2.设总体X属连续型 L(0)=L(,x:0=fx0, i=1 L(0)称为样本的似然函数
似然函数 1.设总体X 属离散型 = = = ( ) ( , , , ; ) ( ; ), 1 1 2 n i L L x x xn p xi L( )称为样本似然函数. 2.设总体 X属连续型 ( ) ( , , , ; ) ( ; ), 1 1 2 = = = n i n xi L L x x x f L( )称为样本的似然函数

概车纶与款理统外「 正态总体均值方差的置信区间与上下限 单个正态总体 1.均值u的置信区间 (1)σ2为已知, 的一个置信水平为灯-的置信区间(X±9n (2)σ2为未知, 的置信水平为1-a的程信区间(±w-
正态总体均值方差的置信区间与上下限 1.均值 的置信区间 单个正态总体 (1) , 2为已知 的一个置信水平为1−的置信区间 . / 2 z n X (2) , 2为未知 的置信水平为1 −的置信区间 ( 1) . / 2 t n − n S X

概華论与款醒硫外 2.方差σ2的置信区间 4未知,方差o2的置信水平为1-ax的置信区间 (n-1)S2n-10s2) za(n-1)'zian(n-1) 标准差σ的一个置信水平为1-α的置信区间 Vn-1S √n-lS yx2n-0’znn-0
1 方差 2 的置信水平为 − 的置信区间 . ( 1) ( 1) , ( 1) ( 1) 2 1 / 2 2 2 / 2 2 − − − − − n n S n n S 2. 方差 2 的置信区间 未知, 标准差 的一个置信水平为1− 的置信区间 . ( 1) 1 , ( 1) 1 2 1 / 2 2 / 2 − − − − − n n S n n S

概车纶与款理统外 两个正态总体 1两个总体均值差山-山2的置信区间 (1)σ2和o22均为已知, 41-h的一个置信水平-a的置信区间 2 X-y±a2n (2)o12和o22均为未知, 4-4的一个置信水平为-的近似置信区间
1. 两个总体均值差1 − 2 的置信区间 (1) , 2 2 2 1 和 均为已知 1 1 − 2的一个置信水平为 −的置信区间 . 2 2 2 1 2 1 / 2 − + n n X Y z 两个正态总体 (2) , 2 2 2 1 和 均为未知 1 1 − 2的一个置信水平为 −的近似置信区间
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《概率论与数理统计》课程教学资源(PPT课件)第七章 参数估计 第七节 单侧置信区间.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第七章 参数估计 第六节 分布参数的区间估计.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第七章 参数估计 第五节 正态总体均值与方差的区间估计.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第七章 参数估计 第四节 区间估计.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第七章 参数估计 第三节 估计量的评选标准.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第七章 参数估计 第二节 基于截尾样本的最大似然估计.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第七章 参数估计 第一节 点估计.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第六章 样本及抽样分布(习题课).ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第六章 样本及抽样分布 第二节 抽样分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第六章 样本及抽样分布 第一节 随机样本.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第五章 大数定律及中心极限定理(习题课).ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第五章 大数定律及中心极限定理 第二节 中心极限定理.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第五章 大数定律及中心极限定理 第一节 大数定律.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第四章 随机变量的数字特征(习题课).ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第四章 随机变量的数字特征 第四节 矩、协方差矩阵.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第四章 随机变量的数字特征 第三节 协方差及相关系数.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第四章 随机变量的数字特征 第二节 方差.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第四章 随机变量的数字特征 第一节 数学期望.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布(习题课).ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 第五节 两个随机变量的函数的分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 随机事件和概率 1.1 随机事件.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 随机事件和概率 1.2 概率的定义.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 随机事件和概率 1.3 条件概率、全概率公式和贝叶斯公式.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 随机事件和概率 1.4 事件的独立性.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 随机事件和概率 1.5 伯努利(Bernoulli)概型.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第一章 随机事件和概率(习题课).ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第二章 随机变量及其分布 2.1 随机变量.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第二章 随机变量及其分布 2.2 离散型随机变量及其分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第二章 随机变量及其分布 2.3 随机变量的分布函数与连续型随机变量.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第二章 随机变量及其分布 2.4 随机变量函数的分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第二章 随机变量及其分布(习题课).ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 3.1 n维随机变量及其分布 3.2 边缘分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 3.1 n维随机变量及其分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 3.2 边缘分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 3.3 条件分布 3.4 相互独立的随机变量.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 3.3 条件分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 3.4 相互独立的随机变量.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 3.5 两个随机变量的函数的分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布 3.5 两个随机变量的函数的分布.ppt
- 《概率论与数理统计》课程教学资源(PPT课件)第三章 多维随机变量及其分布(习题课).ppt
