《数据结构》课程作业习题（无答案）

数据结构精品深程 习题作业 数据结构习题作业 第1章绪论 一、填空题 1数据的逻辑结构是数据元素之间的逻辑关系，通常有下列4类：（)、()、()和()。 2。数据的存储结构是数据在计算机存储器内的表示，主要有四种基本存储为法：（入（人()和（。 3.设待处理问题的规模为，如果一个算法的时问复杂度为一个常数，则表示成数量级的形式为()：如果为 nxog5n,则表示成数量级的形式为()， 4。算法的每一步，必须有确切的定义。也就是说，对于每一步需要执行的动作必须严格、清楚地给出定。这 是算法的()” 5。算法原则上都是能够由机器或人完成的。整个算法好像是一个解决问题的“工作序列”，其中的每一步都是我 们力所能及的一个动作。这是算法的()。 二、选择题 1.假设有如下遗产继承规则：丈夫和妻子可相互继承遗产，子女可继承父亲或母亲的遗产，子女之间不能相互 继承遗产。那么表示该遗产继承关系最合适的数据结构应是（)。 A)树 (B)图 (C线性表 D)集合 2.下面程序段的时间复杂度为()。 for(i-0:1<m:++i) for(j=0;j<n;++j)a[i][j]=i*j; (A)0m2 B)0n2 (C)O(m'n) (D)O(m+n) 3.执行下面程序段，S语句被执行的次数为()人 for(i=0:i<n;++i) for(j=0;j<i;++j)S; (A)n2 (B) (C)n(n+I) (D)n(n-ly2 4。下面算法的时问复杂度为()。 int Ex 1(intn)【 if((n==0)II (n==1))return 1; else return n*Ex 1(n-1): 11/Ex1 (A)O) (B)0n) (C)o(n) 5.使用Ex2(5)调用下而算法时，该算法被调用的总次数为(). int Ex2(intn)【 if(n-=0)return 1; else return n*Ex_2(n-1); 1//Ex2 (A)1 B)2 (C5 (D)6

数据结构精品课程 习题作业 1 数据结构习题作业 第1章 绪论 一、填空题 1．数据的逻辑结构是数据元素之间的逻辑关系，通常有下列4类：（ ）、（ ）、（ ）和（ ）。 2．数据的存储结构是数据在计算机存储器内的表示，主要有四种基本存储方法：（ ）、（ ）、（ ）和（ ）。 3．设待处理问题的规模为n，如果一个算法的时间复杂度为一个常数，则表示成数量级的形式为（ ）；如果为 n×log25n，则表示成数量级的形式为（ ）。 4．算法的每一步，必须有确切的定义。也就是说，对于每一步需要执行的动作必须严格、清楚地给出规定。这 是算法的（ ）。 5．算法原则上都是能够由机器或人完成的。整个算法好像是一个解决问题的“工作序列”，其中的每一步都是我 们力所能及的一个动作。这是算法的（ ）。 二、选择题 1．假设有如下遗产继承规则：丈夫和妻子可相互继承遗产，子女可继承父亲或母亲的遗产，子女之间不能相互 继承遗产。那么表示该遗产继承关系最合适的数据结构应是（ ）。 (A) 树 (B) 图 (C) 线性表 (D) 集合 2．下面程序段的时间复杂度为（ ）。 for(i=0;i<m;++i) for(j=0;j<n;++j) a[i][j]=i*j; (A) O(m2 ) (B) O(n2 ) (C) O(m*n) (D) O(m+n) 3．执行下面程序段，S语句被执行的次数为（ ）。 for(i=0;i<n;++i) for(j=0;j<i;++j) S; (A) n2 (B) n2 /2 (C) n(n+1) (D) n(n-1)/2 4．下面算法的时间复杂度为（ ）。 int Ex_1(int n) { if((n==0)||(n==1)) return 1; else return n*Ex_1(n-1); } // Ex_1 (A) O(1) (B) O(n) (C) O(n2 ) (D) O(n!) 5．使用Ex_2(5)调用下面算法时，该算法被调用的总次数为（ ）。 int Ex_2(int n) { if(n==0) return 1; else return n*Ex_2(n-1); } // Ex_2 (A) 1 (B) 2 (C) 5 (D) 6

数据结构精品课程 习题作业 三、问答颗 1.算法与程序有何异同 2.什么是数据结构？试举一个简单的侧子说明。 3.什么是数据的逻辑结构？什么是数据的存储结构？ 4.什么是算法？算法有哪些特性？ 5.设为正整数，用大“0”表示法如何描述下列程序段的时间复杂度 (1) i=1;k=0: whi1e(i1 wh11e(x>=(y+1)+(y+1))y++: (4) while(i+jj)j++; e13e1++: (5) x=91y-100 while(y>0) 1f(x>100){x=x-10;y-:1 else xt+; 四、算法分析题 1.将下列复杂度由小到大重新排序：2”、nl、n、10000、logn、n×1ogn。 2.求多项式A(x)的算法可以根据下列两个公式之一米设计： (2)A(x)=(+ao 试根据算法的时间复杂度分析比较这两种算法的优劣 3.设有三个函数：n户100m3+n2+1000,gn)-25m'+5000m2,h(n-m545000nlgn.试分析并判断下列关系是否成立： (1)fn=0(g(n)) (2)g(n=Ofn》 (3)hn=0n5 (4)h(n)=O(nlogn) 4.设有丙个算法在同一个机器上运行，其执行时间分别为10Om和2”.如果要使前者快于后者，则至少需要多大 5。有时为了比较两个同数量级算法的优劣，必须突出主项的常数因子，而将低幂次项用大“0”表示。例如，设 Ti(oj=1.39mlgn+100n+256=1.39nlgn+0,To=2.0nlgn-2=2.0lgn+O(o.因为前者的常数因子小于后者，所以当n足够 大时T)优于T,)。试用此方法表示下列函数，并指出当足够大时，哪一个较优，理一个较劣？ 2.3 (2)Ta-=3+1000m+3lg (3)Tn-8m2+3gn (4)T(n)=1.5n+6000nlgn 第2章线性表 一、填空题 1.如果顺序表中第一个元素存储地址是100，每个元素长度为2，则第5个元素存储地址是() 2

数据结构精品课程 习题作业 2 三、问答题 1．算法与程序有何异同？ 2．什么是数据结构？试举一个简单的例子说明。 3．什么是数据的逻辑结构？什么是数据的存储结构？ 4．什么是算法？算法有哪些特性？ 5．设n为正整数，用大“O”表示法如何描述下列程序段的时间复杂度。 （1） i=1; k=0; while(i1 while(x>=(y+1)*(y+1)) y++; （4） i=1; j=0; while(i+jj) j++; else i++; } （5） x=91; y=100; while(y>0) if(x>100) { x=x-10; y-; } else x++; 四、算法分析题 1．将下列复杂度由小到大重新排序：2n 、n!、n2 、10000、log2n、n×log2n。 2．求多项式A(x)的算法可以根据下列两个公式之一来设计： （1）A(x)=anxn +an-1xn-1+.+a1x+a0 （2）A(x)=(.(anx+an-1)x+.+a1)x)+a0 试根据算法的时间复杂度分析比较这两种算法的优劣。 3．设有三个函数：f(n)=100n3 +n2 +1000，g(n)=25n3 +5000n2 ，h(n)=n1.5+5000nlgn。试分析并判断下列关系是否成立： （1）f(n)=O(g(n)) （2）g(n)=O(f(n)) （3）h(n)=O(n1.5) （4）h(n)=O(nlogn) 4．设有两个算法在同一个机器上运行，其执行时间分别为100n2 和2n 。如果要使前者快于后者，则n至少需要多大？ 5．有时为了比较两个同数量级算法的优劣，必须突出主项的常数因子，而将低幂次项用大“O”表示。例如，设 T1(n)=1.39nlgn+100n+256=1.39nlgn+O(n)，T2(n)=2.0nlgn-2n= 2.0lgn+O(n)。因为前者的常数因子小于后者，所以当n足够 大时T1(n)优于T2(n)。试用此方法表示下列函数，并指出当n足够大时，哪一个较优，哪一个较劣？ （1）T1(n)=5n2 -3n+60lgn （2）T2(n)=3n2 +1000n+3lgn （3）T3(n)=8n2 +3lgn （4）T4(n)=1.5n2 +6000nlgn 第2章 线性表 一、填空题 1．如果顺序表中第一个元素存储地址是 100，每个元素长度为 2，则第 5 个元素存储地址是（ ）

数据结构精品课程 习题作业 2.在一个长度为n的顺序表第i(1≤i≤1)个元泰之前插入一个元素，需要向后移动()个元秦，别除第i (1≤i≤)个元素时，需要向前移动()个元素。 3.设单链表中指针p指向结点a。如果要别除a的后继（假设a存在后继），则需要修改指针的操作为()。 4.在由尾指针ar指示的循环链表中表尾插入一个结点s的操作序列是()上刷除开始结点的操作序列为(). 5。在一个具有n个结点的单链表中，在指针p所指结点后插入一个新结点的时问复杂度为()：在给定值为 的结点后插入一个新结点的时间复杂度为()。 二、选择题 1.在长度为n的顺序表中元素c的时间复杂度为(). (A)00 C)O(n (D)O(n2 2。已知线性表L采用顺序存储结构。知果每个元素占用4个存储单元，第9个元素的地址为14，则第1个元素 的地址是()。 (A)108 (B)180 (C176 D)112 3。如果在某个线性表中最常用的操作是选取第i个元素和寻找第个元索的前熏，则采用()存储结构最节省 时问 (A顺序表 (B)单链表 (C)双链表 (①D)单循环链表 4.在具有个结点的有序单链表中插入一个新结点，并仍然保持其有序性的时间复杂度是(). (A)01) (D)O(nlog:) 在个装表中，已想。的结点是p所白的结点的乳，如果在电p之入：所指向的结点，圆 5.在 应该执行()操作。 (A)s->next=p->next;p->next=s. (B)q->next=s;s->next=p; (C)p->next=s->next,s->next-p (D)p->next=s,s->next=q 2.5.3问答题 1,什么时候选用顺序表、什么时候选用链表作为线性表的存储结构为宜？ 2.为什么在单循环链表中设置尾指针比设置头指针史好？ 3.在单链表、循环链表和双向链表中，如果仅知道指针p指向某结点，而不知道头指针，则能否将所指向的 结点从相应的链表中删去？如果可以，则其时间复杂度各为多少 4.在图2-18示的数组A中链接存储着一个线性表，表头指针为A[O]ext,则该线性表是什么？ A 0 4 5 6 data 60564238 2425 exe4376201■ 图2-18线性表的存储结构 5.下述算法的功能是什么？ LinkList Demo(LinkList L)( /川L是无头结点单锁表 if (L&&L->next){ O=L:I=L->next:P=L: while (P->next)P=P->next: P->next=Q;Q->next-NULL return Li /Demo 四、算法设计题 3

数据结构精品课程 习题作业 3 2．在一个长度为 n 的顺序表第 i（1≤i≤n+1）个元素之前插入一个元素，需要向后移动（ ）个元素，删除第 i （1≤i≤n）个元素时，需要向前移动（ ）个元素。 3．设单链表中指针 p 指向结点 a，如果要删除 a 的后继（假设 a 存在后继），则需要修改指针的操作为（ ）。 4．在由尾指针 rear 指示的循环链表中表尾插入一个结点 s 的操作序列是（ ）；删除开始结点的操作序列为（ ）。 5．在一个具有 n 个结点的单链表中，在指针 p 所指结点后插入一个新结点的时间复杂度为（ ）；在给定值为 e 的结点后插入一个新结点的时间复杂度为（ ）。 二、选择题 1．在长度为 n 的顺序表中元素 e 的时间复杂度为（ ）。 (A) O(0) (B) O(1) (C) O(n) (D) O(n2 ) 2．已知线性表 L 采用顺序存储结构，如果每个元素占用 4 个存储单元，第 9 个元素的地址为 144，则第 1 个元素 的地址是（ ）。 (A) 108 (B) 180 (C) 176 (D) 112 3．如果在某个线性表中最常用的操作是选取第 i 个元素和寻找第 i 个元素的前驱，则采用（ ）存储结构最节省 时间。 (A) 顺序表 (B) 单链表 (C) 双链表 (D) 单循环链表 4．在具有 n 个结点的有序单链表中插入一个新结点，并仍然保持其有序性的时间复杂度是（ ）。 (A) O(1) (B) O(n) (C) O(n2 ) (D) O(nlog2n) 5．在一个单链表中，已知 q 所指向的结点是 p 所指向的结点的前驱，如果在 q 和 p 之间插入 s 所指向的结点，则 应该执行（ ）操作。 (A) s->next=p->next; p->next=s; (B) q->next=s; s->next=p; (C) p->next=s->next; s->next=p; (D) p->next=s; s->next=q; 2.5.3 问答题 1．什么时候选用顺序表、什么时候选用链表作为线性表的存储结构为宜？ 2．为什么在单循环链表中设置尾指针比设置头指针更好？ 3．在单链表、循环链表和双向链表中，如果仅知道指针 p 指向某结点，而不知道头指针，则能否将 p 所指向的 结点从相应的链表中删去？如果可以，则其时间复杂度各为多少？ 4．在图 2-18 示的数组 A 中链接存储着一个线性表，表头指针为 A[0].next，则该线性表是什么？ 图 2-18 线性表的存储结构 5．下述算法的功能是什么？ LinkList Demo(LinkList L) { // L是无头结点单链表 if(L&&L->next) { Q=L; L=L->next; P=L; while(P->next) P=P->next; P->next=Q; Q->next=NULL; } return L; } // Demo 四、算法设计题

数据结构精品课程 习题作业 1.试分别用顺序表和单链表作为存储结构，实现将线性表(.，.)就地逆置的操作。所谓“就地”是指辅 助空间应为0(1 2.设顺序表L是一个递减有序表，试设计一个算法：将©插入到L中，并使L仍为一个有序表。 3.设La和Lb是两个单链表，表中元素递增有序，试设计一个算法：将La和Lb就地归并成一个拔元素值递减 有序的单链表L©.请分折算法的时间复杂度。 4.已知一个单链表L,试设计一个算法：将单链表中值重复的结点除，使所得的结果单链表中各结点值均不相 同。 5.假设在长度大于1的循环链表中，既无头结点也无头指针。s为指向循环链表中某个结点的指针，试设计一个 算法：别除s所指向结点的前驱。 第3章栈和队列 一、填空题 1.线性表、栈和队列都属于()结构。可在线性表()位置插入和制除元素：对于栈只能在()插入和 耐除元素：对于队列只能在()插入元素和在（）副除元素， 2.在操作序列push1,Push2,popO.push(5),push(7),popO和push6)之后，栈项元素是（，栈底元素是 3.在操作序s列enqueve1).enqueue(2).dequeuel0,engueue5).enqueue(7刀.dequeue0和enqueue9)之后，队头 元素是()，队尾元素是(). 4.实现递归函数调用的一种数据结构是()。 .在其有个单元的环队中，队满时共有《)个元素 二、选择题 1.如果一个栈的入栈序列是1、23、4、5，则栈不可能的输出序列是(). (A54321 (B45321 (94312 (D)12345 2.如果一个队列的入队顺序是1、2、3、4，则队列的输出顺序是(). (A)4321 (B)1234 (C)1432 D13241 3.在解决计算机主机与打印机之间速度不匹配问题时通常设置一个打印缓冲区，该缓冲区应该是一个()结 构。 (A)钱 (B)队列 (C数组 (D)线性表 4.如果要从栈顶指针为©即的链栈中别除一个结点，用e保存被制除结点的值，则执行()。 (A)c=top,top=top->next, (B)e-opdata next;e=top->dat (D)e-top->dat a top=top->nex 5.设栈S和队列Q的初始状态为空，元素、s、依次通过栈S,一个元素出栈后即进入队列Q 如果6个元素出队的顺序是a、4、a、6、斯、4，则钱S的容量至少应该是(). (A)6 (B)4 93 D)2 三、问答题 1.循环队列的引入是为了克服什么问圈？ 2.设有一个栈，元素进栈的次序为a、b、c,d、e,能否得到出栈序列c、e,a、b、d和cb、a、d、e?如果 能，则写出操作序列：如果不能，则说明原因。 3.如果用QI表示一个循环队列，用o表示队头元泰的 一个位置，用r表示队尾元索的位置，那么队列 4

数据结构精品课程 习题作业 4 1．试分别用顺序表和单链表作为存储结构，实现将线性表（a0, a1, . an-1）就地逆置的操作。所谓“就地”是指辅 助空间应为 O(1)。 2．设顺序表 L 是一个递减有序表，试设计一个算法：将 e 插入到 L 中，并使 L 仍为一个有序表。 3．设 La 和 Lb 是两个单链表，表中元素递增有序，试设计一个算法：将 La 和 Lb 就地归并成一个按元素值递减 有序的单链表 Lc，请分析算法的时间复杂度。 4．已知一个单链表 L，试设计一个算法：将单链表中值重复的结点删除，使所得的结果单链表中各结点值均不相 同。 5．假设在长度大于 1 的循环链表中，既无头结点也无头指针。s 为指向循环链表中某个结点的指针，试设计一个 算法：删除 s 所指向结点的前驱。 第3章 栈和队列 一、填空题 1．线性表、栈和队列都属于（ ）结构。可在线性表（ ）位置插入和删除元素；对于栈只能在（ ）插入和 删除元素；对于队列只能在（ ）插入元素和在（ ）删除元素。 2．在操作序列 push(1)，push(2)，pop()，push(5)，push(7)，pop()和 push(6)之后，栈顶元素是（ ），栈底元素是 （ ）。 3．在操作序列 enqueue(1)，enqueue(2)，dequeue()，enqueue(5)，enqueue(7)，dequeue()和 enqueue(9)之后，队头 元素是（ ），队尾元素是（ ）。 4．实现递归函数调用的一种数据结构是（ ）。 5．在具有 n 个单元的循环队列中，队满时共有（ ）个元素。 二、选择题 1．如果一个栈的入栈序列是 1、2、3、4、5，则栈不可能的输出序列是（ ）。 (A) 54321 (B) 45321 (C) 43512 (D) 12345 2．如果一个队列的入队顺序是 1、2、3、4，则队列的输出顺序是（ ）。 (A) 4321 (B) 1234 (C) 1432 (D) 3241 3．在解决计算机主机与打印机之间速度不匹配问题时通常设置一个打印缓冲区，该缓冲区应该是一个（ ）结 构。 (A) 栈 (B) 队列 (C) 数组 (D) 线性表 4．如果要从栈顶指针为 top 的链栈中删除一个结点，用 e 保存被删除结点的值，则执行（ ）。 (A) e=top; top=top->next; (B) e=top->data; (C) top=top->next; e=top->data; (D) e=top->data; top=top->next; 5．设栈 S 和队列 Q 的初始状态为空，元素 a1、a2、a3、a4、a5、a6依次通过栈 S，一个元素出栈后即进入队列 Q。 如果 6 个元素出队的顺序是 a2、a4、a3、a6、a5、a1，则栈 S 的容量至少应该是（ ）。 (A) 6 (B) 4 (C) 3 (D) 2 三、问答题 1．循环队列的引入是为了克服什么问题？ 2．设有一个栈，元素进栈的次序为 a、b、c、d、e，能否得到出栈序列 c、e、a、b、d 和 c、b、a、d、e？如果 能，则写出操作序列；如果不能，则说明原因。 3．如果用 Q[n]表示一个循环队列，用 front 表示队头元素的前一个位置，用 rear 表示队尾元素的位置，那么队列

数据结构精品课程 习恩作业 中元素个数是多少？ 、n,其输出序列为PI、P2、P、.、P,如果p,则是多少 :品果利个根1和52恢拟个似列，那么应该如何利用栈的运算实现风列的插入和 四、算法设计题 1.试设计一个算法：判定给定的字符向量是否为回文，回文即正读和反读均相同的字符序列，比如字符序列“b” 和字符序列“abdb阳”均是回文，但字符序列“g0od”不是回文。提示：将一半字符入栈.。 2.试设计一个算法：判断一个算术表达式的圆括号是否正确配对，提示：采用栈的结构，对表达式进行扫错时， 凡遇到字符“(”就进栈，遇到字符“)”就退栈，表达式扫描完毕后栈应该为空。 3.假设以带头结点的循环链表表示队列，且只设一个指针指向队尾元素。试设计一个算法：对该循环队列进行 置空队、判队空、入队和出队操 4.假设顺序栈S中有2个元素，从栈顶到栈底的元素依次为，21，·、1。试设计一个算法：通过一个得 环队列Q重新排列该栈中的元煮，使得从栈顶到栈底的元素依次为。、.、1小、.、·要求空间 复杂度和时间复杂度均为O) 5.假设编号为1、2.3、4的四列火车通过一个如图3-2所示 的铁路调度站，可能得到的调度结果有康些？如果 有列火车通过调度站，试设计一个算法：输出所有可能的调度结果。 第4章串 一、填空题 1,空申与空格申的区别在于( 2.两个学符串相等的充分必要条件是〔) 3.设S=1 am a teacther,其长度为()。 4.在KMP算法中，模式T向右滞动的位置k与主串(). 5.模式"abaabcac""的ne函数值序列为()。 二、选择题 1.设有两个申p和q,求q在p中首次出现的位置的运算称作()。 B)桓式匹配 (C求子串 D)求串长 其特殊性体现在()。 (A)可以顺序存储 (B)数据元素是一个字符 (C可以诗式存储 D)数据元素可以是多个字符 3.在顺序串中，根据空间分配方式的不同，可以分为(). 直接分配和间接分配 B)静态分配和动态分配 (©顺序分配和链式分配 (D)随机分配和周定分配 4.下列关于申的叙述中，正确的是（)。 (A)一个串的字符个数即该串的长度 ®)一个串的长度至少是1 (©空串是由一个空格字符组成的串 (D)如果两个串S1和S2长度相同，则这两个串相等 5.设中S1=ABCDEFG",S2=PORST:通过连接操作StrConcat(&TS1.S2)返回S1和S2连接而成的新串T. 通过求子申操作SubString(&Sub.S,i,j)返回S从第i个字符起长度为j的子串Sub,通过求长度操作SteLengthe(S)返回S

数据结构精品课程 习题作业 5 中元素个数是多少？ 4．已知一个栈的入栈序列是 1、2、3、.、n，其输出序列为 p1、p2、p3、.、pn，如果 p1=n，则 pi 是多少？ 5．如果利用两个栈 S1 和 S2 模拟一个队列，那么应该如何利用栈的运算实现队列的插入和删除操作？ 四、算法设计题 1．试设计一个算法：判定给定的字符向量是否为回文。回文即正读和反读均相同的字符序列，比如字符序列“abba” 和字符序列“abdba”均是回文，但字符序列“good”不是回文。提示：将一半字符入栈。 2．试设计一个算法：判断一个算术表达式的圆括号是否正确配对。提示：采用栈的结构，对表达式进行扫描时， 凡遇到字符“(”就进栈，遇到字符“)”就退栈，表达式扫描完毕后栈应该为空。 3．假设以带头结点的循环链表表示队列，且只设一个指针指向队尾元素。试设计一个算法：对该循环队列进行 置空队、判队空、入队和出队操作。 4．假设顺序栈 S 中有 2n 个元素，从栈顶到栈底的元素依次为 a2n、a2n-1、.、a1。试设计一个算法：通过一个循 环队列 Q 重新排列该栈中的元素，使得从栈顶到栈底的元素依次为 a2n、a2n-2、.、a2、a2n-1、a2n-3、.、a1。要求空间 复杂度和时间复杂度均为 O(n)。 5．假设编号为 1、2、3、4 的四列火车通过一个如图 3-2 所示的铁路调度站，可能得到的调度结果有哪些？如果 有 n 列火车通过调度站，试设计一个算法：输出所有可能的调度结果。 第4章 串 一、填空题 1．空串与空格串的区别在于（ ）。 2．两个字符串相等的充分必要条件是（ ）。 3．设 S="I_am_a_teacther"，其长度为（ ）。 4．在 KMP 算法中，模式 T 向右滑动的位置 k 与主串（ ）。 5．模式"abaabcac"的 next 函数值序列为（ ）。 二、选择题 1．设有两个串 p 和 q，求 q 在 p 中首次出现的位置的运算称作（ ）。 (A) 连接 (B) 模式匹配 (C) 求子串 (D) 求串长 2．串是一种特殊的线性表，其特殊性体现在（ ）。 (A) 可以顺序存储 (B) 数据元素是一个字符 (C) 可以链式存储 (D) 数据元素可以是多个字符 3．在顺序串中，根据空间分配方式的不同，可以分为（ ）。 (A) 直接分配和间接分配 (B) 静态分配和动态分配 (C) 顺序分配和链式分配 (D) 随机分配和固定分配 4．下列关于串的叙述中，正确的是（ ）。 (A) 一个串的字符个数即该串的长度 (B) 一个串的长度至少是 1 (C) 空串是由一个空格字符组成的串 (D) 如果两个串 S1 和 S2 长度相同，则这两个串相等 5．设串 S1="ABCDEFG"，S2="PQRST"：通过连接操作 StrConcat(&T, S1, S2)返回 S1 和 S2 连接而成的新串 T， 通过求子串操作 SubString(&Sub, S, i, j)返回 S 从第 i 个字符起长度为 j 的子串 Sub，通过求长度操作 SteLength(S)返回 S

数据结构精品课程 习题作业 的长度：那么执行操作SubConcat(T,SubString(Sub1,S,2,StrLength(S2.SubString(Sub2,SL,StrLength(S2,2m后，T 是（) (A)BCDEF (B)BCDEFG (C)BCPORST (D)BCDEFEF 三、问答题 1.下列每对术语的区别是什么？ (1)串变量和串常量： (2)主串和子中： (3)串名和串值 2。顺序串静态分配和动态分配的特点分别是什么？ 3.设串S="Iam a student" T="good”,Q='worker (I)SubString(Sub.S.8.刀操作后，Sb的结果是什么 (2)SubString(Sub.T2,1)作后，Sub的结果是什么？ (3)StrReplace(S,&,7,Q)操作后，S的结果是什么？ (4)StrConcat(,SubString(Sub1,S,6,2.StrConcat(B,T.SubString(Sub2,S,7,8操f作后，A的结果是什么g 4.已知串S="(yz+,T="(x+z内y",利用StrConcat、SubString和StrReplace操作如何将S转化为T? 5.下列串的nct函数值是什么？ （1T=mah, (3)T="aaabcaab" (4)T=abcaabbabcabaacbacba". 四、算法设计题 1.试设计一个算法：将子串T插入主串S第pOs个位置上. 2.试设计一个算法：除申S中第0s个字符开始的t个字符。 3.试设计一个算法：用子串T替换主串s中第个字符开始m个字符枸成的子串。 4.试设计一个算法：求解串S和T的最长公共子申 5.如果一个文本串使用事先给定的字母映射表进行加密。例如，设字母映射表如图41山所示 n g=qt c ob m u h e 1 x p d ax f y:vr s3 图411字母映射表 则串enryp"被加密为kzwsdf.试设计一个算法 ()将输入的文本串进行加密后输出： (2)将输入的已加密的文本串进行解密后输出】 第5章数组和广义表 一、填空题 6

数据结构精品课程 习题作业 6 的长度；那么执行操作 SubConcat(T, SubString(Sub1, S1, 2, StrLength(S2)), SubString(Sub2, S1, StrLength(S2), 2)))后，T 是（ ）。 (A) BCDEF (B) BCDEFG (C) BCPQRST (D) BCDEFEF 三、问答题 1．下列每对术语的区别是什么？ （1）串变量和串常量； （2）主串和子串； （3）串名和串值。 2．顺序串静态分配和动态分配的特点分别是什么？ 3．设串 S="I am a student"，T="good"，Q="worker"： （1）SubString(Sub, S, 8, 7)操作后，Sub 的结果是什么？ （2）SubString(Sub, T, 2, 1) 作后，Sub 的结果是什么？ （3）StrReplace(S, 8, 7, Q)操作后，S 的结果是什么？ （4）StrConcat(A, SubString(Sub1, S, 6, 2), StrConcat(B, T, SubString(Sub2, S, 7, 8)))操作后，A 的结果是什么？ 4．已知串 S="(xyz)+*"，T="(x+z)*y"，利用 StrConcat、SubString 和 StrReplace 操作如何将 S 转化为 T？ 5．下列串的 next 函数值是什么？ （1）T="aaab"； （2）T="abcabaa"； （3）T="aaabcaab"； （4）T="abcaabbabcabaacbacba"。 四、算法设计题 1．试设计一个算法：将子串 T 插入主串 S 第 pos 个位置上。 2．试设计一个算法：删除串 S 中第 pos 个字符开始的 t 个字符。 3．试设计一个算法：用子串 T 替换主串 S 中第 n 个字符开始 m 个字符构成的子串。 4．试设计一个算法：求解串 S 和 T 的最长公共子串。 5．如果一个文本串使用事先给定的字母映射表进行加密。例如，设字母映射表如图4-11所示： 图 4-11 字母映射表 则串"encrypt"被加密为"tkzwsdf"。试设计一个算法： （1）将输入的文本串进行加密后输出； （2）将输入的已加密的文本串进行解密后输出。 第5章 数组和广义表 一、填空题

数据结构精品课程 习题作业 1,数组通常只有两种基本运算：()和()。这决定了数组通常采用()结构来实现存储。 2.二维数组A中行下标从10到20列下标从5到10.如果按行优先存储，每个元素占4个存储单元，AN10I5) 的存储地址是1000，则元素A1510)的存储地址是(). 3.设有一个10阶的对称矩阵A,如果采用压缩存储，A0O为第一个元素，其存储地址为LOC(0小，每个元素 的长度是1个字节，则元素A8[5]的存饮地址为()。 4.广义表LSa,(b.c以(@，其长度是()，深度是()表头是()。表尾是()。 5.广义表LSa,b,c,d.e,如果采用函数GetHead和GetTail取出LS中的原子b,则运算是()。 二、选坪题 1.将数组称为随机存取结构是因为()。 (A数组元素是随机的 (B)对数组任一元素存取时间相等 (C随时可以对数组进行访问 D)数组的存储结构是不定 2.二雏数组A的每个元素是8个学节组成的双精度实数，行下标的范围是07刀，列下标的范围是0-9列，则存放 A至少需要《)个字节。 (A80 (B)144 (C)504 (D)640 3.对特殊矩阵采用压缩存储的目的主要是为了()。 (A)表达变得简单 (B)对矩阵元素的存取变得简单 D)减少不必要的存储空间 (A)0 B)(O) (C(0.0) ①)0.0.0) 5.下面的说法中，不正确的是()， (A)广义表是一种多层次的结构 B)广义表是一种非线性结构 (©广义表是一种共享结构 D)广义表是一种递归 三、问答题 1.特殊矩阵和稀疏矩陈哪一种压缩存储后会失去随机存取的功能？为什么？ 2.数组、广义表与线性表之何有什么样的关系？ 3.设一个二维 组A56的每个元素占4个字节，已知L0C(am10O0,那么A共占多少个字节？A的终端 点as的起始地址是多少？当按行和按列优先存储时，2s的起始地址分别为多少？ 4.分别画出下列广义表的图形表示： (1)A(a.B(b.d).C(e.B(b.d).L(C.g (2)A(a,B(b.A)) 5.下列广义表运算的结果是什么 (1)GetHead(GetTail(((a.b).(c.d).(e.f)))) (2)GetTail(GetHead(((a,b),(c.d)(e,f)))) (3GetHead(GetTail(GetHead((ab).) (4)GetTail(GetHead(GietTail (((ab) (5)GetTail(GetTail(GetHead (((a,b).(e,f))))) 四、算法设计题 .如果在矩阵A中存在一个元素a,(0≤i≤n,0j≤m-1),该元素是第i行元素中最小值且又是第j列元素中 最大值，则称此元素为该矩阵的一个马鞍点。假设以二维数组常规存储矩阵A,试设计一个算法：求解该矩阵的所有 马撒点。 2.已知两个x的对称矩阵按压缩存储方法存储在一维数组A和B中，试设计一个算法：求解对称矩阵的乘积 3.试设计一个算法：创建稀疏矩阵的十字链表， 4.试设计一个算法：求解一个广义表所拥有的原子结点个数 7

数据结构精品课程 习题作业 7 1．数组通常只有两种基本运算：（ ）和（ ），这决定了数组通常采用（ ）结构来实现存储。 2．二维数组 A 中行下标从 10 到 20，列下标从 5 到 10，如果按行优先存储，每个元素占 4 个存储单元，A[10][5] 的存储地址是 1000，则元素 A[15][10]的存储地址是（ ）。 3．设有一个 10 阶的对称矩阵 A，如果采用压缩存储，A[0][0]为第一个元素，其存储地址为 LOC(a00)，每个元素 的长度是 1 个字节，则元素 A[8][5]的存储地址为（ ）。 4．广义表 LS=((a), (((b), c)), (d))，其长度是（ ），深度是（ ），表头是（ ），表尾是（ ）。 5．广义表 LS=(a, (b, c, d), e)，如果采用函数 GetHead 和 GetTail 取出 LS 中的原子 b，则运算是（ ）。 二、选择题 1．将数组称为随机存取结构是因为（ ）。 (A) 数组元素是随机的 (B) 对数组任一元素存取时间相等 (C) 随时可以对数组进行访问 (D) 数组的存储结构是不定 2．二维数组 A 的每个元素是 8 个字节组成的双精度实数，行下标的范围是[0~7]，列下标的范围是[0~9]，则存放 A 至少需要（ ）个字节。 (A) 80 (B) 144 (C) 504 (D) 640 3．对特殊矩阵采用压缩存储的目的主要是为了（ ）。 (A) 表达变得简单 (B) 对矩阵元素的存取变得简单 (C) 去掉矩阵中的多余元素 (D) 减少不必要的存储空间 4．如果广义表 LS 满足 GetHead(LS)=GetTail(LS)，则 LS 为（ ）。 (A) () (B) (()) (C) ((), ()) (D) ((), (), ()) 5．下面的说法中，不正确的是（ ）。 (A) 广义表是一种多层次的结构 (B) 广义表是一种非线性结构 (C) 广义表是一种共享结构 (D) 广义表是一种递归 三、问答题 1．特殊矩阵和稀疏矩阵哪一种压缩存储后会失去随机存取的功能？为什么？ 2．数组、广义表与线性表之间有什么样的关系？ 3．设一个二维数组 A[5][6]的每个元素占 4 个字节，已知 LOC(a00)=1000，那么 A 共占多少个字节？A 的终端结 点 a45的起始地址是多少？当按行和按列优先存储时，a25 的起始地址分别为多少？ 4．分别画出下列广义表的图形表示： （1）A(a, B(b, d), C(e, B(b, d), L(f, g))) （2）A(a, B(b, A)) 5．下列广义表运算的结果是什么？ （1）GetHead(GetTail(((a, b), (c, d), (e, f)))) （2）GetTail(GetHead(((a, b), (c, d), (e, f)))) （3）GetHead(GetTail(GetHead (((a, b), (e, f))))) （4）GetTail(GetHead(GetTail (((a, b), (e, f))))) （5）GetTail(GetTail(GetHead (((a, b), (e, f))))) 四、算法设计题 1．如果在矩阵 A 中存在一个元素 aij（0≤i≤n-1，0≤j≤m-1），该元素是第 i 行元素中最小值且又是第 j 列元素中 最大值，则称此元素为该矩阵的一个马鞍点。假设以二维数组常规存储矩阵 A，试设计一个算法：求解该矩阵的所有 马鞍点。 2．已知两个 n×n 的对称矩阵按压缩存储方法存储在一维数组 A 和 B 中，试设计一个算法：求解对称矩阵的乘积。 3．试设计一个算法：创建稀疏矩阵的十字链表。 4．试设计一个算法：求解一个广义表所拥有的原子结点个数

数据结构精品课程 习题作业 5.试设计一个算法：创建广义表的头尾链表。 第6章树和二叉树 一、填空题 1.有一棵二叉树如图6-47所示：这棵树的根结点是()，这棵树的叶子结点是《)，结点k3的度是()。 这棵树的度是 ,这棵树的树高是（)，结点k3的孩子是()，结点k3的父亲是（)。 ②®⊙ 图6-47二叉树 2.深度为k的完全二叉树，至少包括()个结点，至多包括(）个结点：如果具有个结点的完全二叉树 按照层序从】开始编号，则编号最小的叶子结点序号是()， 3.一棵二叉树的第i(i≥1)层最多有()个结点：一棵有n(>0)个结点的满二叉树共有()个叶子结 点和()个非终端结点」 4.某二义树的先序遍历序列是ABCDEFG,中序遍历序列是CBDAFGE,则其后序送历序列是(. 5.在具有n个结点的二叉链表中，共有()个指针域，其中()个指针域用于指向其左右孩子，剩下的() 个指针域则是空的。 二、选择题 .用顺序存储的方法将完全二叉树中的所有结点逐层存放在数组A小A中，如果结点A有左子树，则左子 树的根结点是() (A)A2i-11 B)A2i+11 D)A21 2.设、m为一棵二又树上的两个结点，在中序老历时，n在m之前的条件是() (A)n在m上方 (B)n是m祖先 (C)n在m左方 (D)n是m子孙 3.任何一棵二叉树的叶子结点在先序、中序、后序遍历序列中的相对次序()。 A》肯定不发生改变 B)肯定发生改变 (C有时发生变化 D)不能确定 4.如果T是由一棵有序树T转换而来的一棵二叉树，那么T中结点的先序序列就是T中结点的()序列，T 中结点的后序序列藏是T中结点的()序列。 (A)先序 B)中序 (C后序 D)层序 5.如果森林中有4棵树，树中结点的个数依次为、，则把森林转换成二叉树后，其根结点的右子树 上有()个结点，根结点的左子树上有()个结点。 (A)n-1 (B)n (C)n+n+n3 (D)n:+ng+na 三、问答题

数据结构精品课程 习题作业 8 5．试设计一个算法：创建广义表的头尾链表。 第6章 树和二叉树 一、填空题 1．有一棵二叉树如图 6-47 所示：这棵树的根结点是（ ），这棵树的叶子结点是（ ），结点 k3 的度是（ ）， 这棵树的度是（ ），这棵树的树高是（ ），结点 k3 的孩子是（ ），结点 k3 的父亲是（ ）。 图6-47 二叉树 2．深度为 k 的完全二叉树，至少包括（ ）个结点，至多包括（ ）个结点；如果具有 n 个结点的完全二叉树 按照层序从 1 开始编号，则编号最小的叶子结点序号是（ ）。 3．一棵二叉树的第 i（i≥1）层最多有（ ）个结点；一棵有 n（n＞0）个结点的满二叉树共有（ ）个叶子结 点和（ ）个非终端结点。 4．某二叉树的先序遍历序列是 ABCDEFG，中序遍历序列是 CBDAFGE，则其后序遍历序列是（ ）。 5．在具有 n 个结点的二叉链表中，共有（ ）个指针域，其中（ ）个指针域用于指向其左右孩子，剩下的（ ） 个指针域则是空的。 二、选择题 1．用顺序存储的方法将完全二叉树中的所有结点逐层存放在数组 A[1]~A[n]中，如果结点 A[i]有左子树，则左子 树的根结点是（ ）。 (A) A[2i-1] (B) A[2i+1] (C) A[i/2] (D) A[2i] 2．设 n、m 为一棵二叉树上的两个结点，在中序遍历时，n 在 m 之前的条件是（ ）。 (A) n在m上方 (B) n是m祖先 (C) n在m左方 (D) n是m子孙 3．任何一棵二叉树的叶子结点在先序、中序、后序遍历序列中的相对次序（ ）。 (A) 肯定不发生改变 (B) 肯定发生改变 (C) 有时发生变化 (D) 不能确定 4．如果 T'是由一棵有序树 T 转换而来的一棵二叉树，那么 T 中结点的先序序列就是 T'中结点的（ ）序列，T 中结点的后序序列就是 T'中结点的（ ）序列。 (A) 先序 (B) 中序 (C) 后序 (D) 层序 5．如果森林中有 4 棵树，树中结点的个数依次为 n1、n2、n3、n4，则把森林转换成二叉树后，其根结点的右子树 上有（ ）个结点，根结点的左子树上有（ ）个结点。 (A) n1-1 (B) n1 (C) n1+ n2+ n3 (D) n2+n3+n4 三、问答题

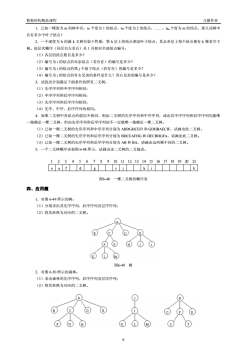
数据结构精品课程 习题作业 1.已知一棵度为m的树中有：个度为1的结点，个度为2的结点，几个度为m的结点，那么该树中 共有多少个叶了结点？ 2. 一个深度为h的满k叉树有如下性质：第h层上的结点都是叶子结点，其余各层上每个结点都有k棵非空子 树。按层次顺序（同层自左至右）从1开始对全部结点编号： (1)各层的结点数目是多少？ (2)编号为1的结点的双亲结点（若存在）的编号是多少？ (3)编号为ⅰ的结点的第j个孩子结点（若存在）的编号是多少 (4)编号为1的结点的有右兄弟的条件是什么？其右兄弟的编号是多少？ 3.试找出分别满足下面条件的所有二叉树： (1)先序序列和中序序列相同： (2)中序序列和后序序列相同： (3)先序序列和后序序列相同： (4)先序、中序、后序序列均相同。 4.如果二叉树中各结点的值均不相同，则由二叉树的先序序列和中序序列，或由其中序序列和后序序列均能唯 一地确定一棵二又树，但由先序序列和后序序列却不一定能唯一地确定一保二又树 (I)已知一棵二叉树的先序序列和中序序列分别为ABDGHCEFI和GDHBAECIF,试画出此二叉树， (2)己知一棵二义树的先序序列和后序序列分别为BDCEAFHG和DECBHGFA,试通出此二义树。 (3)已知一棵二叉树的先序序列和后序序列分别为AB和BA,请画出这两棵不同的二叉树。 5.一个二义树顺序表如图648所示，试画出该二义树的二叉链表 123456789101112131415161718192021 。a■d■gcib 图6-48一棵二又树的顺序表 四、应用题 1.对图6-49所示的树 (1)分别求出其先序序列、后序序列及层序序列： (2)将其转换为对应的二叉树 ®⊙®①① ⑧3①④ 图6-49树 2.对图6-50所示的森林 ()求出森林的先序序列、后序序列及层次序列： (2)将其转换为对应的二叉树。 ⊙ N ⊙ ⊙® 包⊙⑧ ®①M 9

数据结构精品课程 习题作业 9 1．已知一棵度为 m 的树中有：n1个度为 1 的结点，n2个度为 2 的结点，.，nm 个度为 m 的结点，那么该树中 共有多少个叶子结点？ 2．一个深度为 h 的满 k 叉树有如下性质：第 h 层上的结点都是叶子结点，其余各层上每个结点都有 k 棵非空子 树。按层次顺序（同层自左至右）从 1 开始对全部结点编号： （1）各层的结点数目是多少？ （2）编号为 i 的结点的双亲结点（若存在）的编号是多少？ （3）编号为 i 的结点的第 j 个孩子结点（若存在）的编号是多少？ （4）编号为 i 的结点的有右兄弟的条件是什么？其右兄弟的编号是多少？ 3．试找出分别满足下面条件的所有二叉树： （1）先序序列和中序序列相同； （2）中序序列和后序序列相同； （3）先序序列和后序序列相同； （4）先序、中序、后序序列均相同。 4．如果二叉树中各结点的值均不相同，则由二叉树的先序序列和中序序列，或由其中序序列和后序序列均能唯 一地确定一棵二叉树，但由先序序列和后序序列却不一定能唯一地确定一棵二叉树。 （1）已知一棵二叉树的先序序列和中序序列分别为 ABDGHCEFI 和 GDHBAECIF，试画出此二叉树。 （2）已知一棵二叉树的先序序列和后序序列分别为 BDCEAFHG 和 DECBHGFA，试画出此二叉树。 （3）已知一棵二叉树的先序序列和后序序列分别为 AB 和 BA，请画出这两棵不同的二叉树。 5．一个二叉树顺序表如图 6-48 所示，试画出该二叉树的二叉链表。 图6-48 一棵二叉树的顺序表 四、应用题 1．对图 6-49 所示的树： （1）分别求出其先序序列、后序序列及层序序列； （2）将其转换为对应的二叉树。 图6-49 树 2．对图 6-50 所示的森林： （1）求出森林的先序序列、后序序列及层次序列； （2）将其转换为对应的二叉树

数据结构精品课程 习想作业 图650森林 3.对给定的一组权值W-(5.2,9,1L.8.3,7),试构造相应的哈夫曼树，并计算其带权路径长度。 4.已知某字符串S中共有8种字符，各种字符出现的概率分别是2次、1次、4次、5次、7次、3次、4次和9 次，对串S用0,1进行前缀编码，试计算该字符串的编码位数。 5.假设用于通信的电文由学符集a,dc,￡gb中的字母构成，这8个字母在电文中出现的概分别为007， 0.19,0.020.06.0.32,0.03,0.21,0.101- (1)试为这8个字母设计哈夫曼编码。 (2)如果用3位二进制数对这8个字母进行等长编码，则哈夫曼编码的平均码长是等长编码的百分之几？它使 电文总长平均压缩多少？ 五、算法设计题 1.试设计一个算法：分别采用递归和非递归方法后序卷历二叉树. 2.试设计一个算法：交换一颗二又树中每个结点的左孩子和右孩子 3。试设计一个算法：计算二义树的叶子结点数 4.试设计一个算法：判断一棵二叉树是否为完全二叉树。 5.试设计一个算法：在二叉树中查找值为：的结点，并输出©的所有祖先。假设二叉树中值为：的结点不多于1 第7章图 一、填空题 1.已知一个无向图用邻接矩阵表示，第i个顶点的度是()片己知一个有向图用邻接矩阵表示，第】个顶点的 度是(). 2.设无向图G1中顶点数为，那么G1至少有()条边，至多有()条边：设有向图G2中顶点数为n,那 么图G2至少有()条弧，至多有()条弧. 3.图的深度优先遍历类似于树的()遍历，它所用到的数据结构是()：图的广度优先遍历类似于树的(） 遍历，它所用到的数据结构是()。 4.对于含有n个顶点©条边的连通图，如果利用普里姆算法求最小生成树，则时问复杂度为（：如果利用克 色斯卡尔算法求最小生成树，则时间复杂度为()， 5.如果一个有向图不存在()，则该图的全部顶点可以挂列成一个拓扑序列。 二、选择题 1,n个顶点的无向完全图有()条边：n个顶点的有向完全图有(）条弧。 (A)n-1)2 (B)nn-1) (C)n(n+1y2 D)2 2.G是一个非连通无向图，共有28条边，则该图至少有()个顶点。 (B)7 (C)8 (D)9 定一个有肉腿是春事南除了用法林，柔可 (A)广度优先遍历法 ()深度优先遍历法 (C)求关键路径法 (D)求最短路径法 4.最小生成树指的是()。 (A)由连通网所得到的边数最少的生成树 (⑧)由连通网所得到的顶点数相对较少的生成树 10

数据结构精品课程 习题作业 10 图6-50 森林 3．对给定的一组权值 W=(5, 2, 9, 11, 8, 3, 7），试构造相应的哈夫曼树，并计算其带权路径长度。 4．已知某字符串 S 中共有 8 种字符，各种字符出现的概率分别是 2 次、1 次、4 次、5 次、7 次、3 次、4 次和 9 次，对串 S 用[0, 1]进行前缀编码，试计算该字符串的编码位数。 5．假设用于通信的电文由字符集{a, b, c, d, e, f, g, h}中的字母构成，这 8 个字母在电文中出现的概率分别为{0.07, 0.19, 0.02, 0.06, 0.32, 0.03, 0.21, 0.10}。 （1）试为这 8 个字母设计哈夫曼编码。 （2）如果用 3 位二进制数对这 8 个字母进行等长编码，则哈夫曼编码的平均码长是等长编码的百分之几？它使 电文总长平均压缩多少？ 五、算法设计题 1．试设计一个算法：分别采用递归和非递归方法后序遍历二叉树。 2．试设计一个算法：交换一颗二叉树中每个结点的左孩子和右孩子。 3．试设计一个算法：计算二叉树的叶子结点数。 4．试设计一个算法：判断一棵二叉树是否为完全二叉树。 5．试设计一个算法：在二叉树中查找值为 e 的结点，并输出 e 的所有祖先。假设二叉树中值为 e 的结点不多于 1 个。 第7章 图 一、填空题 1．已知一个无向图用邻接矩阵表示，第 i 个顶点的度是（ ）；已知一个有向图用邻接矩阵表示，第 i 个顶点的 度是（ ）。 2．设无向图 G1 中顶点数为 n，那么 G1 至少有（ ）条边，至多有（ ）条边；设有向图 G2 中顶点数为 n，那 么图 G2 至少有（ ）条弧，至多有（ ）条弧。 3．图的深度优先遍历类似于树的（ ）遍历，它所用到的数据结构是（ ）；图的广度优先遍历类似于树的（ ） 遍历，它所用到的数据结构是（ ）。 4．对于含有 n 个顶点 e 条边的连通图，如果利用普里姆算法求最小生成树，则时间复杂度为（ ）；如果利用克 鲁斯卡尔算法求最小生成树，则时间复杂度为（ ）。 5．如果一个有向图不存在（ ），则该图的全部顶点可以排列成一个拓扑序列。 二、选择题 1．n 个顶点的无向完全图有（ ）条边；n 个顶点的有向完全图有（ ）条弧。 (A) n(n-1)/2 (B) n(n-1) (C) n(n+1)/2 (D) n2 2．G 是一个非连通无向图，共有 28 条边，则该图至少有（ ）个顶点。 (A) 6 (B) 7 (C) 8 (D) 9 3．判定一个有向图是否存在回路除了可以利用拓扑排序方法外，还可以用（ ）。 (A) 广度优先遍历法 (B) 深度优先遍历法 (C) 求关键路径法 (D) 求最短路径法 4．最小生成树指的是（ ）。 (A) 由连通网所得到的边数最少的生成树 (B) 由连通网所得到的顶点数相对较少的生成树