《力学》课程教学资源（作业习题）材料力学习题解

材料力学习题 第一章绪论 P10,1-4 己知：=100mm,△/=5x102mm 求：平均应变 解： E-45x10-mm P14,1-5 已知：g=0.03mm 求：ey,7B。 求：OB平均应变：B点ABC角度改变 解： 1-5 a=00=25x10- -2g(8）-25x0 P14,1-6 己知：圆形薄板，R=80.00mm,△R=3×103mm。求：￡响，Y向e 求：径向平均应变：周向平均应变： 解： E径前=△R/R=3.75×10- 5w贤 2πR

材料力学习题 第一章 绪论 P10，1-4 已知：l=100mm，Δl =5×10-2mm。 求：平均应变 解： mm l l 4 5 10− =    = P14，1-5 已知：vB=0.03mm 求：εby，γB。 求：OB 平均应变；B 点 ABC 角度改变 解： 1-5 1-6 1 4 4 2.5 10 ' 2 2 2.5 10 − − −  =       = − = =  OB OA tg OB v B B yB    P14，1-6 已知：圆形薄板，R=80.00mm，ΔR=3×10-3mm。求：ε 径向，γ 周向。 求：径向平均应变；周向平均应变； 解： 周向 径向 径向       =  = +  − = =  =  − R R R R R R R R 2 2 ( ) 2 / 3.75 10 5

材料力学习题 第二章拉压与剪切 孙训芳 22F1 F22F125 P44,2-1 绘轴力图。 2 F 解： F F 如图。 F 2 2 a F d P44,2-2 3 绘轴力图。A0.0004m2,求各截面应力。 3 -F-50 MPa 10kN 如国，学=-5m P45,2-3 ,320kN210kN120kN 绘轴力图。A1=0.0002m2,A-0.0003m2,A:=0.0004m2,求各截 应力。 13 解 10kN -10 MPa 如图。oea-52=-383M Co -F-=2 MPa P45,2-6 F=10kN,4=0.0001m2,=0°，30°， 45°，60°，90°，求各斜截面应力 如图。 Xw

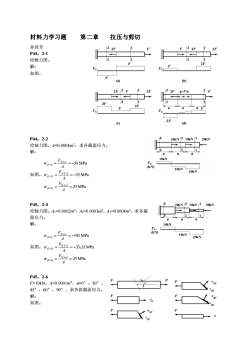
材料力学习题 第二章 拉压与剪切 孙训芳 P44，2-1 绘轴力图。 解： 如图。 P44，2-2 绘轴力图。A=0.0004m2，求各截面应力。 解： 如图。 25 MPa 25 MPa 50 MPa N 3 3 (3 3) N 2 2 (2 2) N1 1 (1 1) = = = = − = = − − − − − − − A F A F A F    P45，2-3 绘轴力图。A1=0.0002m2，A2=0.0003m2，A3=0.0004m2，求各截 面应力。 解： 如图。 25 MPa 33 33 MPa 100 MPa N 3 3 (3 3) N 2 2 (2 2) N1 1 (1 1) = = = = − = = − − − − − − − A F A F A F    。 P45，2-6 F=10kN，A=0.0001m2，α=0°，30°， 45°，60°，90°，求各斜截面应力。 解： 如图

=-=100 MPa=0 =c cos30*=75 MPa =o sin=43.30 MPa 6g=6cos245°=50MPTg=6sim45°cos45=50MPa a=G cos60*=25 MPa =a sin 60*cos60*=43.30 MPa 0w=6c0s290°=0tw=6sn90°c0s90°=0 P45,2-8 b0.2m,E=10GPa,作轴力图，求各段应力、应变，总变形。 解： 1轴力如图。 2各段应力、应变 a2MP an6MPs c=g=-25x106c=可=-65x10- 3总变形 M=Wc+c=-3.75x10-9.75x10=-135×103m P46,2-11 已知a,F,E,4。求CD的距离改变△cD 解： 1横向应变 e台 2CD的距离改变△cD Ac-CD=-1. P46,2-12 己知：AB刚性，杆1、2、3材质相同E=210GPa =1m =4=00001m2 As=0.00015m F=20kN。试求C的水平、铅垂位移 解： 1内力 2变形 2 2 EA 2EA =4.7×10m2= =4.762×10m3=0 EA,2EA 3位移

cos 90 0 sin 90 cos90 0 cos 60 25 MPa sin 60 cos 60 43.30 MPa cos 45 50 MPa sin 45 cos 45 50 MPa cos 30 75 MPa sin 30 cos30 43.30 MPa 100 MPa 0 90 2 90 60 2 60 45 2 45 30 2 30 0 0 = = = = = = = = = = = = = = = = = = = =                                          A F P45，2-8 b=0.2m，E=10GPa，作轴力图，求各段应力、应变，总变形。 解： 1 轴力如图。 2 各段应力、应变 4 4 N N 2.5 10 6.5 10 2.5 MPa 6.5MPa − − = = −  = = −  = = − = = − E E A F A F AC BC AC AC BC BC AC AC       3 总变形 3.75 10 9.75 10 1.35 10 m −4 −4 −3 l = l AC +lBC = −  −  = −  P46，2-11 已知 a，δ，F，E，μ。求 CD 的距离改变ΔCD。 解： 1 横向应变 EA F  ' = − 2 CD 的距离改变ΔCD     E F EA F CD CD a 4  = ' = −1.003 = −1.003 P46，2-12 已知：AB 刚性，杆 1、2、3 材质相同 E=210GPa， l=1m ， A1=A2=0.0001m2 ， A3=0.00015m2 ， F=20kN。试求 C 的水平、铅垂位移。 解： 1 内力 0 2 2 N1 = N 2 = FN 3 = F F F F 2 变形 4.762 10 m 0 2 4.762 10 m 2 3 4 2 1 N 2 2 4 1 1 N1  1 = = =   = = =   = − − l EA Fl EA F l l EA Fl EA F l l 3 位移

A点位移 6=M,=4.762×10m-→)6=-d，=-4.762×10m) B点位移 6=-4M2=-4.762×10°m) C点位移 。=d=472x0-m)66-8-47a×10m山 2 P47,2-17 己知：两杆长度、截面和材质都相同。试求两杆应变能之比。 解 内力 Fu-F F:-fx 2应变能 2EA P48,2-21 己知：AB、AD两杆材质相同，[o小I7OMP 截面各为两根等边角钢。试选择型号。 307 解： 1内力 F-300 kNF0600 N 2m 2选择等边角钢型号 器销-10m AD杆选择No.80×6,AB杆选择No.100×10。 P49,2-25(1) 己知：AC、BD两杆材质相同，[d=17OMPa,E=210GPa:截面圆形， d=0.025m,=0.018m:F=100kN,并记其作用点为F点。试校核强度， 计算两杆变形，以及A、B两点的铅垂位移。 解 1内力 3m 人1-25=667w人：-号-33w 2校核强度

A 点位移 4.762 10 m( ) 4.762 10 m( ) 4 1 4 =  1 =  → = − = −   − − l l  Ax  Ay B 点位移 4.762 10 m( ) 4 = − 2 = −   − l  By C 点位移 4.762 10 m( ) 2 4.762 10 m( ) 4 4 = −   + = =  → = − Ay By − Cx Ax Cy      P47，2-17 已知：两杆长度、截面和材质都相同。试求两杆应变能之比。 解： 1 内力 x l F FN1 = F FN 2 = 2 应变能 3 2 6 d 2 2 d 2 1 2 0 2 N1 2 2 0 2 N1 1 = = = = =       V V EA F l EA F x V EA F l EA F x V l l P48，2-21 已知：AB、AD 两杆材质相同，[σ]=170MPa， 截面各为两根等边角钢。试选择型号。 解： 1 内力 600 kN sin 30 300 kN N N = N = =  AD AD AB F F F 2 选择等边角钢型号         N N 3 2 N N 4 2 1.765 10 m 2 2 8.824 10 m 2 2 − − =   =  =   =        AB AB AB AB AB AD AD AD AD AD F A A F F A A F AD 杆选择 No.80×6，AB 杆选择 No.100×10。 P49，2-25(1) 已知：AC、BD 两杆材质相同，[σ]=170MPa，E=210GPa；截面圆形， d1=0.025m，d2=0.018m；F=100kN，并记其作用点为 F 点。试校核强度， 计算两杆变形，以及 A、B 两点的铅垂位移。 解： 1 内力 33.33 kN 3 66.67 kN 3 2 N1 = = N 2 = = F F F F 2 校核强度

。e-经=ssMsb]o经=H0Nm<间 满足强度要求。 3计算两杆变形 4、B两点的铅垂位移分别等于两杆变形。 P49,2-25(2) 将F作用于A,试计算F点的铅垂位移。 解： 1内力 ,=F=100kNF2=0 2计算两杆变形 3计算F点的铅垂位移 ,-2=167x10m P49,2-28 己知：如图薄壁管长度为b,材料弹性模量为E,内压为P,试计算管壁周向应 力，内半径的伸长。 解 1内力 Fx=rpb 2计算管壁周向应力 希-罗 3计算内半径的伸长 心6话

         = =  = = 131.0 MPa  4 135.8MPa 4 2 2 N 2 2 1 N1 d F d F AC BD 满足强度要求。 3 计算两杆变形 1.559 10 m 4 1.617 10 m 4 3 2 2 N 2 2 3 2 1 N1 1 − −  = =   = =  E d F l l E d F l l   A、B 两点的铅垂位移分别等于两杆变形。 P49，2-25(2) 将 F 作用于 A，试计算 F 点的铅垂位移。 解： 1 内力 FN1 = F =100 kN FN 2 = 0 2 计算两杆变形 2.425 10 m 0 4 2 3 2 1 N1  1 = =   = − l E d F l l  3 计算 F 点的铅垂位移 1.617 10 m 3 2 1 −3 =   = l  Fy P49，2-28 已知：如图薄壁管长度为 b，材料弹性模量为 E，内压为 p，试计算管壁周向应 力，内半径的伸长。 解： 1 内力 FN = rpb 2 计算管壁周向应力      rp b rpb b F = = = N 3 计算内半径的伸长    E r p r r 2  = =

刘鸿文 P54,2-1 绘轴力图」 40KN 30kN 20kN 解： 2-2 如图。 10kN P54,2-4 F 己知：BC的直径上10mm,F=7.5kN 3m 1.5m1.5m 求：BC的应力。 解： ∑Mo=0 1.5Fx+4.5F=3F ∑ME=0 0.75Fx-1.5f=0 Fy =6kN Fy =3kN 0=号-等=76w P55,2-5 已知：杆1、2的直径d=10mm,dh=20mm:载荷 F=10kN。 求：两杆的应力。 2。 先求内力：拆去杆1、2，代以FN、FN2, ∑M4=0F=0 ∑Mg=02F1=Fx ∑y=0F+Fx1=Fx2 FM=F FN2 =2F w=5 A =127Mn =63.7na P55,2-6 已知：杆的直径左10mm,受拉力F=10kN。 求：ā为30°斜截面上的应力。 解： Ga=G cos230=95.9MPa t0=osin30°cos30°=55.1MPa P55,2-7

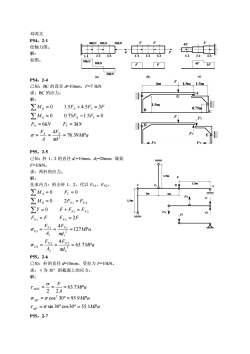
刘鸿文 P54，2-1 绘轴力图。 解： 如图。 P54，2-4 已知：BC 的直径 d=10mm，F=7.5kN 求：BC 的应力。 解： MPa d F A F F k N F k N M F F M F F F N N N Y E N Y D N Y 76.39 4 6 3 0 0.75 1.5 0 0 1.5 4.5 3 2 = = = = = = − = = + =     P55，2-5 已知：杆 1、2 的直径 d1=10mm，d2=20mm；载荷 F=10kN。 求：两杆的应力。 解： 先求内力：拆去杆 1、2，代以 FN1、FN2， MPa d F A F MPa d F A F F F F F Y F F F M F F M F N N N N N N N N B N N A Y 63.7 4 127 4 2 0 0 2 0 0 2 2 2 2 2 (2) 2 1 1 1 1 (1) 1 2 1 2 1 2 = = = = = = = = = + = = = = =        P55，2-6 已知：杆的直径 d=10mm，受拉力 F=10kN。 求：α为 30°斜截面上的应力。 解： MPa MPa MPa A F o o MAX sin 30 cos30 55.1 cos 30 95.9 63.7 2 2 30 2 30 =   = =  = = = =       P55，2-7

已知：油缸内径D-350mm,内压p1MPa,螺栓许用应川o]=40MPa. ：螺栓直径d 解 内力年个银花R=P忍6=1604W 设计直径： o=Fw/A=4Fw/d2≤[o] 4F d2a-0259m P57,2-12 已知：4=l0cm2,【o]=7MPa,4=6cm,[o]=160MPa. ：合理允许载荷 钢杆2 解 1.内力：F,=-V3F,F2=2F 30°7入 2.极载估算： 木杆1 Cu-Fal_fiF slok =FsloA=404IkN-F 4 o=2 3 :无-花sak3Fs4-48w-5 3.结论：[F]=mm{E,F}=F P57,2-15 己知：斜截面60°，A=4cm2,[a小=100MPa,[d=50MPa。 求：可使F达到最大的a和此时F 解： 在斜截面上： .=cosiaslal 乙-snwowast] 分别可以得： A cos a cosa sin a Ao] 同时：Fmco263650kN DA P59,2-17

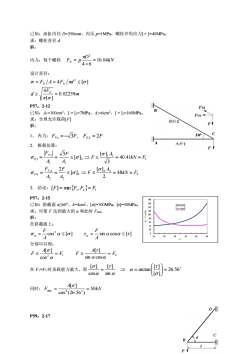
已知：油缸内径 D=350mm，内压 p=1MPa，螺栓许用应力[σ]=40MPa。 求：螺栓直径 d 解： 内力：每个螺栓 kN D FN p 16.04 4 6 2 =  =  设计直径： m F d F A F d N N N 0.02259 [ ] 4 4 [ ] 2  = = =       P57，2-12 已知：A1=100cm2，[σ]1=7MPa，A2=6cm2，[σ]1=160MPa。 求：合理允许载荷[F] 解： 1． 内力： FN1 = − 3F, FN 2 = 2F 2． 极载估算： 2 2 2 2 2 2 2 (2) 1 1 1 2 1 1 1 (1) 48 2 [ ] [ ] 2 40.41 3 [ ] [ ] 3 k N F A F A F A F k N F A F A F A F N N = =    = = = =    = =       3． 结论：  1 2  1 [F] = min F ,F = F P57，2-15 已知：斜截面 α≤60°，A=4cm2，[σ]=100MPa，[τ]=50MPa。 求：可使 F 达到最大的 α 和此时 Fmax 解： 在斜截面上： cos [ ] sin cos [ ] 2         =   =  A F A F 分别可以得： 2 1 2 sin cos [ ] cos [ ] F A F F A F  =  =      在 F1=F2 时承载能力最大，即  26.56 [ ] [ ] arctan sin [ ] cos [ ] =        =  =        同时： kN A F 50 cos (26.56 ) [ ] max 2 = =   P59，2-17 0 20 40 60 80 100 120 140 160 180 10 20 30 40 50 60 α° F 1、F 2 (kN) F1= F2=

已知：两杆材质相同，许用应力为σ]。 求：可使整个结构用材体积达到最小的0， 1内力：记斜杆为杆1，水平杆为杆2，三日F2=-FC0s8 sin 2.强度： w40-oa-8-ol→4=o6468 FI FIcos0 Fl(1+cos20) 3.体积：V=4从+，可sm8cs0+a]sm0可]m0cos6 4体极小：80-0-2n0cas0-6+cos0lka20-sm0-0 -sin20cos20-cos20+sin20-cos0=0-cos20-cos20+sin20=0 解出：0=54.74 P61,2-29 己知：钢索A=76.36mm㎡，长度单位0.4m,载荷F=20kN,弹模 E=177GPa。 ：C点铅垂位移。 解 1.内力：∑M,=0 9r2a+5r4a-Fa-=0 N=5=15W 2应a=导=1513wm 3总伸长：=5,4=1367×10m EA 5能量法-报189×0广m

已知：两杆材质相同，许用应力为[σ]。 求：可使整个结构用材体积达到最小的 θ。 解： 1. 内力：记斜杆为杆 1，水平杆为杆 2，    sin cos sin 2 1 1 F F F FN = ； N = − 2. 强度：             [ ]sin cos [ ]sin [ ] sin cos [ ] sin 1 2 1 (2) 1 (1) F A F A A F A F = = ； = =  = ； = 3. 体积： ( )           [ ]sin cos 1 cos [ ]sin cos [ ]sin cos 2 1 1 2 2 + = + = + = Fl Fl Fl V A l A l 4. 体积极小值： 0 2sin cos (1 cos )(cos sin ) 0 2 2 2 2 2 =  − − + − =         V sin cos cos sin cos 0 cos cos sin 0 2 2 2 2 4 2 2 2 −   −  +  −  =  −  −  +  = 解出：   = 54.74 P61，2-29 已知：钢索 A=76.36mm2，长度单位 a=0.4m，载荷 F=20kN，弹模 E=177GPa。 求：C 点铅垂位移。 解： 1. 内力： M A = 0 kN F FN FN a FN a F a 11.55 3 4 3 0 2 3 2 2 3 = = + − = 2. 应力： MPa A FN  = =151.3 3. 总伸长： m EA F a l N 3 1.367 10 4 −  = =  4. C 点铅垂位移： m v v l v B D C 4 7.892 10 2 2sin 60 − =   = + =  5. 能量法： m EA Fa v EA F a EA F a Fv C N C 4 2 2 7.892 10 3 4 3 2 2 4 2 1 − = = = = 

P63,2-39 己知：四根角钢为杆1，总面积A=1.216×103m2,弹模E1=200GPa [o]=160MPa,木柱为杆2，=-6.25×10m2 ,弹模=10GPa [o]2=12MPa. 求：合理允许载荷[F门。 解 1平：F1+F2=F a E14=0.3891 E2A 2.协：60-Ga, F 4解.R=4。F=-0280IFF:-+aF=0719F 5.极载估算： 新1.0aFs240-6a6N=万 F F 按杆2a年4+0o→F≤0+a四4@10418N=月 6.结论：[F]=mm{F,F}=F P63,2-40 已知：受力、约束入图。 求：两端反力。 解： 1.平：Fw1=F+Fw2 2.协：M,+W2=0 1你管密05或：a名 4解R6F-06F

P63，2-39 已知：四根角钢为杆 1，总面积 A1=1.216×10-3m2，弹模 E1=200GPa， [σ]1=160MPa，木柱为杆 2，A2=6.25×10-2m2，弹模 E2=10GPa， [σ]2=12MPa。 求：合理允许载荷[F]。 解： 1. 平： 0.3891 2 2 1 1 1 2 + = = = E A E A FN FN F  2. 协： (1) (2)  =  3. 物： 1 2 2 1 2 2 2 1 1 1 N N N 2.5699 N N N F F F F E A F E A F = = = 4. 解： FN F F FN F 0.7199F 1 1 0.2801 1 1 2 = + = = + =    5. 极载估算： 按杆 1 1 1 1 1 1 (1) 694.6 (1 ) [ ] [ ] (1 ) k N F A F A F A FN = = +    + = =        按杆 2 2 2 2 2 2 (2) [ ] (1 ) [ ] 1041.8 (1 ) F A k N F A F A FN    + = = + = =      6. 结论： 1 2 1 [F] = min{ F ,F } = F P63，2-40 已知：受力、约束入图。 求：两端反力。 解： 1. 平： FN1 F FN 2 = + 2. 协： l 1 + l 2 = 0 3. 物： a b F F EA F b EA F a N N N N + = = −  = 1 2 1 2 0 4. 解： F a b a F F a b b FN N + − = + = 1 2 5. 反力：  +  = + = F a b a F F a b b FRA RB

P65,2-44 1m 己知：先记长度单位a=1m,杆1长h,面积A=60×10m2, 杆2长=2h,面积A=120×10m2:E=E=E2,F=6kN。 求：试计算各杆内力和A点反力。 解： 1.平：FN,+2Fw2=3F FNI FN 2.协：2Y1=W2 ,:2-5即R= EA EA 4解：E2-9F=72NF1-F=36W 5.A点反力：Ra=0R=F-F1-FN2=-4.8kN) P69,2-58 d=10mm,D=80mm,[t]=60MPa. 解： 1男力加片=品=120N 2i年-导=5现<g全 P70,2-62 已知：F=630kNm,t=200MPa,6=0.02m 求：试计算D。 F F=0.05013m 剪切：r8=.→D P71,2-65 已知：b-012m h0.35m,c-0.045m,F=40kN. 求：试计算剪切、挤压应力。 解： 1m h=09524MPa

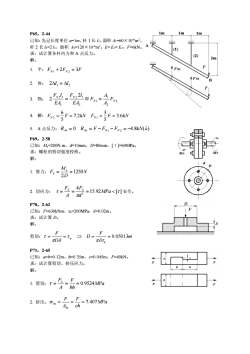
P65，2-44 已知：先记长度单位 a=1m，杆 1 长 l1，面积 A1=60×10-6m2， 杆 2 长 l2=2 l1，面积 A2=120×10-6m2 ；E= E1= E2，F=6kN。 求：试计算各杆内力和 A 点反力。 解： 1. 平： FN1 + 2FN 2 = 3F 2. 协： 2 1 2 l = l 3. 物： 2 2 1 1 1 1 2 2 EA F l EA F l N N = 即 2 2 1 N1 FN A A F = 4. 解： FN F k N FN F 3.6k N 5 3 7.2 5 6 2 1 = = = = 5. A 点反力： 0 4.8 ( ) RAx = RAy = F − FN1 − FN 2 = − kN  P69，2-58 已知：Me=200N.m，d=10mm，D=80mm，[τ]=60MPa。 求：螺栓的剪切强度校核。 解： 1. 剪力： N D M F e S 1250 2 = = 2. 切应力： 15.92 [ ] 4 2    = = = MPa  d F A FS S 安全。 P70，2-62 已知：F=630kNm，τu=200MPa，δ=0.02m。 求：试计算 D。 解： 剪切： m F D D F u = = u  = = 0.05013      P71，2-65 已知：a=b=0.12m，h=0.35m，c=0.045m，F=40kN。 求：试计算剪切、挤压应力。 解： 1. 剪切： MPa bh F A FS  = = = 0.9524 2. 挤压： MPa ch F A F bs  bs = = = 7.407