《力学》课程教学资源（PPT课件）材料力学——扭转

第三章 扭转 第一节 概述 扭转是杆件的基本变形之一。 1.受力特点 杆件受绕轴线旋转的力偶或力偶系的作用，这些 力偶的旋转平面都垂直于杆件的轴线。 2.变形特点 横截面绕轴线旋转，两横截面间产生相对角位移， 称扭转角φ，纵向线段变形为螺旋线，与变形前的夹角 称为剪切角Y。 M Me 第三章扭转

第三章 扭转 1 第三章 扭转 第一节 概述 扭转是杆件的基本变形之一。 1. 受力特点 杆件受绕轴线旋转的力偶或力偶系的作用，这些 力偶的旋转平面都垂直于杆件的轴线。 2. 变形特点 横截面绕轴线旋转，两横截面间产生相对角位移， 称扭转角φ，纵向线段变形为螺旋线，与变形前的夹角 称为剪切角γ。 M e M e  

第二节薄壁圆简的扭转 1.试验曲线 纯剪切试验：薄壁圆管，纯扭转，长度为，中面 半径为，厚度为δ。在实验中发现，材料在纯剪切变 形过程中，也会呈现出弹性和强化的力学行为。对于 许多碳素钢材，在弹性和强化阶段之间还会出现明显 的屈服。 Me 第三章扭转

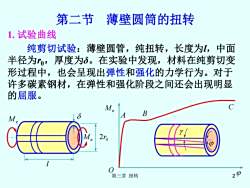
第三章 扭转 2 第二节 薄壁圆筒的扭转 1. 试验曲线 纯剪切试验：薄壁圆管，纯扭转，长度为l，中面 半径为r0，厚度为δ。在实验中发现，材料在纯剪切变 形过程中，也会呈现出弹性和强化的力学行为。对于 许多碳素钢材，在弹性和强化阶段之间还会出现明显 的屈服。 M e M e 2 0 r  l   O M e  A B C

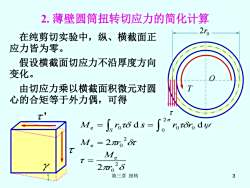
2.薄壁圆筒扭转切应力的简化计算 2ro 在纯剪切实验中，纵、横截面正 应力皆为零。 假设横截面切应力不沿厚度方向 变化。 由切应力乘以横截面积微元对圆 心的合矩等于外力偶，可得 7 Me=人nδds=∫。"oody M。=2m,26 Me 2m。26 第三章扭转 3

第三章 扭转 3 2. 薄壁圆筒扭转切应力的简化计算 在纯剪切实验中，纵、横截面正 应力皆为零。 假设横截面切应力不沿厚度方向 变化。 由切应力乘以横截面积微元对圆 心的合矩等于外力偶，可得          2 0 e 2 e 0 2 0 e 0 0 0 2 2 d d r M M r M r s r r S = = = =     '  O 2 0 r  T

3.切应变，剪切胡克定律 剪切角Y即为切应变，圆管两端的相对扭转角为φ， 小变形时切应变为 在纯剪切试验的弹性阶段中的线弹性段，φ正比例 于T,于是切应变正比例于切应力，即 -Gy 这个关系称剪切胡克定律。定律中的比例常数G称切 变模量，是材料的弹性系数。对于各向同性材料，E、 4、G三个弹性系数之间存在下式关系 E G= 21+4)） 第三章扭转 4

第三章 扭转 4 3. 切应变，剪切胡克定律 剪切角γ即为切应变，圆管两端的相对扭转角为φ， 小变形时切应变为 在纯剪切试验的弹性阶段中的线弹性段，φ正比例 于T，于是切应变正比例于切应力，即 这个关系称剪切胡克定律。定律中的比例常数G称切 变模量，是材料的弹性系数。对于各向同性材料，E、 μ、G三个弹性系数之间存在下式关系  = G   l r0 = ( + ) = 2 1 E G

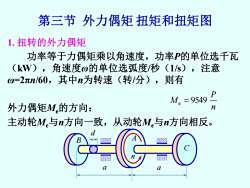
第三节外力偶矩扭矩和扭矩图 1.扭转的外力偶矩 功率等于力偶矩乘以角速度，功率P的单位选千瓦 (kW)，角速度w的单位选弧度/秒(1s)，注意 w=2πnl/60,其中n为转速（转/分），则有 M。=9549 外力偶矩M的方向： n 主动轮M与n方向一致，从动轮M。与n方向相反

第三节 外力偶矩 扭矩和扭矩图 1. 扭转的外力偶矩 功率等于力偶矩乘以角速度，功率P的单位选千瓦 （kW），角速度ω的单位选弧度/秒（1/s），注意 ω=2πn/60，其中n为转速（转/分），则有 外力偶矩Me的方向： 主动轮Me与n方向一致，从动轮Me与n方向相反。 n P Me = 9549 B A a a C n d

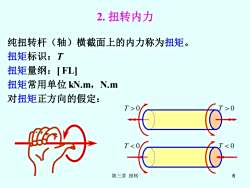
2.扭转内力 纯扭转杆（轴）横截面上的内力称为扭矩。 扭矩标识：T 扭矩量纲：[FL 扭矩常用单位kN.m,N.m 对扭矩正方向的假定： 第三章扭转

第三章 扭转 6 2. 扭转内力 纯扭转杆（轴）横截面上的内力称为扭矩。 扭矩标识：T 扭矩量纲：[ FL] 扭矩常用单位 kN.m，N.m 对扭矩正方向的假定： T  0 T  0 T  0 T  0

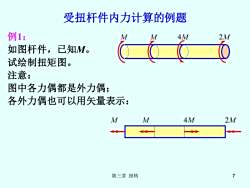
受扭杆件内力计算的例题 例1： 4M 2M 如图杆件，已知M。 试绘制扭矩图。 注意： 图中各力偶都是外力偶； 各外力偶也可以用矢量表示： M M 4M 2M 第三章扭转 7

第三章 扭转 7 受扭杆件内力计算的例题 例1： 如图杆件，已知M。 试绘制扭矩图。 注意： 图中各力偶都是外力偶； 各外力偶也可以用矢量表示： M M 4M 2M M M 4M 2M

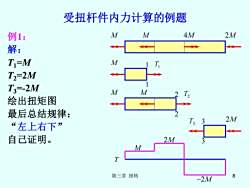
受扭杆件内力计算的例题 例1： M 4M 2M 解： T=M T2=2M T3=-2M 绘出扭矩图 最后总结规律： 2M “左上右下” 自己证明。 第三章扭转 8 -2M

第三章 扭转 8 受扭杆件内力计算的例题 例1： 解： T1=M T2=2M T3=-2M 绘出扭矩图 最后总结规律： “左上右下” 自己证明。 M M 4M 2M M 1 T1 1 M M 2 T2 2 T3 3 3 2M M T 2M −2M

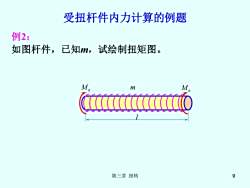
受扭杆件内力计算的例题 例2： 如图杆件，已知m,试绘制扭矩图。 M m M O 第三章扭转 9

第三章 扭转 9 受扭杆件内力计算的例题 例2： 如图杆件，已知m，试绘制扭矩图。 M e m M e l

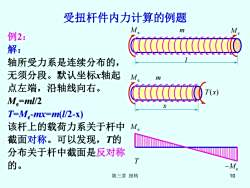
受扭杆件内力计算的例题 M M 例2： 解： 轴所受力系是连续分布的， 无须分段。默认坐标x轴起 点左端，沿轴线向右。 M.=ml/2 (女u T=M.-mx=m(l/2-x) 该杆上的载荷力系关于杆中 M 截面对称。可以发现，T的 分布关于杆中截面是反对称 的。 Me 第三章扭转 10

第三章 扭转 10 受扭杆件内力计算的例题 例2： 解： 轴所受力系是连续分布的， 无须分段。默认坐标x轴起 点左端，沿轴线向右。 Me =ml/2 T=Me -mx=m(l/2-x) 该杆上的载荷力系关于杆中 截面对称。可以发现，T的 分布关于杆中截面是反对称 的。 M e m M e l M e m x T(x) T M e −Me