《信号与系统》课程教学课件(PPT讲稿)§3.5 典型非周期信号的频谱

心号与系型 §3,5典型张周期信号的 傅里叶变换 矩形脉浊 单边指数信号 直流信号 符号函数 ·升金弦脉冲信号 新疆大学信息科学与工程学院电子系 2011.1 退出 开始
新疆大学信息科学与工程学院电子系 2011.1 §3.5 典型非周期信号的 傅里叶变换 •矩形脉冲 •单边指数信号 •直流信号 •符号函数 •升余弦脉冲信号

一,矩形脉冲信号 P-”a= e-jor 2 2 -jo @t jo Et e2-e 2 sin 2 -x/20x/2 2j @t 2 2 2 幅度频谱:|F(o)=ESao? 2 0<o<2+h 相位频谱:p(o)= 2n+h<o<2m+2办 n=0,1,2
X 第 2 一.矩形脉冲信号 页 ( ) − − = 2 2 j e d F E t t 2 2 j e j − − − = E t 2 j e e . 2 2 j 2 j − − = E 2 2 sin = E = 2 Sa E ( ) = 2 Sa 幅度频谱: F E 相位频谱: ( ) ( ) ( ) ( ) 0,1,2, 2 2 1 π 2 2 2 π π 4 π 2 2 1 π 0 = + + + = n n n n n E O f (t) t − 2 2
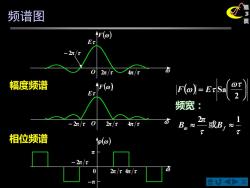
频谱图 F(@) 2/2 幅度频谱 F(@) Et F@)=EtSa 频宽: 2n/t An t 或B, 相位频谱 2n/t 2n/t Ant
X 第 3 页 2π 1 B 或Bf 频谱图 ( ) = 2 Sa 幅度频谱 F E 相位频谱 频宽: F() E − 2π O 2π 4π () 0 2π 4π − 2π π −π F() E O 2π 4π − 2π

二.单边指数信号 Ee-a t>0 a>0 f@) f)= E t风
X 第 4 页 ( ) ( ) − − − = = E u t t F f t t t e e d ( ) j F ( ) = − 0 0 e 0 0 t E t f t t 二.单边指数信号 ( ) j e d 0 j + = = − + E E t t f (t) O t E
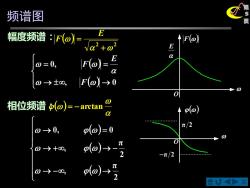
频谱图 幅度频谱:F(o)= E vato' FO) E a 0=0, 0→士0, F(@)→0 0 相位频谱(o)=-arctan p(@ 0→0, p(o)=0 元/2 0 po)→-于 π/2 0-→-00, po)→ 2 合心通
X第5 频谱图 页 ( ) 2 2 + = E F ( ) ( ) → → = = , 0 0 , F E F ( ) = −arctan ( ) ( ) ( ) → − → → + → − → = 2π , 2π , 0, 0 幅度频谱: 相位频谱: F() OE O () − π 2 π 2

三.直流信号 f(t)=E,-o0<t<+oo 不满足绝对可积 E←→2πEδ(o) 条件,不能直接 用定义求F(O) f( T→∞ s() E
X 第 6 页 f (t) = E,− t + 三.直流信号 不满足绝对可积 条件,不能直接 用定义求 F() O t f (t) 1 − E → E 2π E () O t f (t) E

推导 F(@)=lim[Ee-i'dt F) t→0 e-jot Flim (2E) T→0 -jw e-ior- Flim T→∞ -jw E2血E6@) 2sin(@t) Elim 时域无限宽,频带无限窄 T-→0 ⊙ 2 Elim t sin(ot) lim-Sa(@)-5(@) T0∞ 元 Wt 证明 =2mEδ(o) 合U通
X 第 7 推导 页 F( ) E t t e d j lim − − → = − − = − → j e j lim t E j e e j j lim − − = − → E ( ) 2sin lim → = E ( ) sin π 2π lim → = E = 2π E () O (2π E) F() E 2π E () Sa( ) ( ) π lim = → 时域无限宽,频带无限窄

四.符号函数 不满足绝对 0=sn0)- +1, t>0 可积条件 sgn(t) t<0 -at e 处理方法:做一个双边函数 at fd)=sgn(t)ea,求F(o 求极限得到F(o) ro-。eed+心e'eo'di -j2ω a-jo'a+jo a'+a2 F(o)=limF(O)-limao -j20 2 X-0 -jo
X 第 8 页 t 1 − 1 sgn(t) O ( ) − + = = 1, 0 1, 0 ( ) sgn t t f t t 四.符号函数 处理方法: ( ) − − − − = − + 0 j 0 j F1 e e dt e e dt t t t t 2 2 j2 j 1 j 1 + − = + + − − = ( ) ( ) j j2 2 2 2 0 1 0 lim lim = + − = = → → F F t e − t e − ( ) ( ) ( ) 求极限得到 ( )。 , 求 , F f t t F t 1 1 sgn e − = 做一个双边函数 不满足绝对 可积条件

频谱图 t)jo-i 2 F(@) 2 ro-日-d ⊙ F(o是偶函数 p(o) 元 2 >0 0 arctan 0<0 2 2 p(o)是奇函数
X 第 9 页 ( ) 2 j e 2 2 j j 2 sgn t = − = 频谱图 F()是偶函数 ()是奇函数 O 2 π 2 π − () 2 F() O ( ) = = 2 2 2 F − = − , 0 2 π , 0 2 π 0 2 arctan

五.升余弦脉冲信号 0-w fr() 0≤fs r(o)=f(t)-i"dt 】 t d
X 第 10 五.升余弦脉冲信号 页 ( ) = + t E t f t 0 π 1 cos 2 O t E f (t) − 2 E 2 − 2 F( ) f (t) t t e d j − − = t E t t e d π 1 cos 2 j − − = + − − − − − − − = + + t E t E t E t t t t t e e d 4 e e d 4 e d 2 j j j j j ( ) + + = + − π Sa 2 π Sa 2 Sa E E E
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《信号与系统》课程教学课件(PPT讲稿)§3.4 非周期信号的频谱分析─傅里叶变换.ppt
- 《信号与系统》课程教学课件(PPT讲稿)频谱图.ppt
- 《信号与系统》课程教学课件(PPT讲稿)狄利克雷条件.ppt
- 《信号与系统》课程教学课件(PPT讲稿)周期信号的功率证明.ppt
- 《信号与系统》课程教学课件(PPT讲稿)冲激序列的频谱不满足收敛性.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§3.3 典型周期信号的傅里叶级数.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§3.1 引言.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§3.2 周期信号的频谱分析——傅里叶级数.ppt
- 《信号与系统》课程教学课件(PPT讲稿)证明交换律.ppt
- 《信号与系统》课程教学课件(PPT讲稿)微积分性质的证明.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§2.7 卷积的性质.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§2.6 卷积.ppt
- 《信号与系统》课程教学课件(PPT讲稿)定初始条件.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§2.5 冲激响应和阶跃响应.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§2.4 零输入响应和零状态响应.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§2.3 起始点的跳变.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§2.2 微分方程式的建立与求解.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§2.1 引言.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§1.8 系统分析方法.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§1.7 线性时不变系统.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§3.6 冲激函数和阶跃函数的傅里叶变换.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§3.7 傅里叶变换的性质.ppt
- 《信号与系统》课程教学课件(PPT讲稿)奇偶虚实性证明.ppt
- 《信号与系统》课程教学课件(PPT讲稿)尺度变换性质 证明.ppt
- 《信号与系统》课程教学课件(PPT讲稿)时域微分性质证明.ppt
- 《信号与系统》课程教学课件(PPT讲稿)时域积分性质证明.ppt
- 《信号与系统》课程教学课件(PPT讲稿)时移加尺度变换证明.ppt
- 《信号与系统》课程教学课件(PPT讲稿)等效脉冲宽度与等效频带宽度.ppt
- 《信号与系统》课程教学课件(PPT讲稿)例3-7-10(时域积分).ppt
- 《信号与系统》课程教学课件(PPT讲稿)例3-7-1(对称性).ppt
- 《信号与系统》课程教学课件(PPT讲稿)例3-7-2(对称性).ppt
- 《信号与系统》课程教学课件(PPT讲稿)例3-7-4(时移性质,教材3-2).ppt
- 《信号与系统》课程教学课件(PPT讲稿)例3-7-5(时移,尺度).ppt
- 《信号与系统》课程教学课件(PPT讲稿)例3-7-6教材例3-4.ppt
- 《信号与系统》课程教学课件(PPT讲稿)例3-7-7(时域微分).ppt
- 《信号与系统》课程教学课件(PPT讲稿)例3-7-8(频域微分).ppt
- 《信号与系统》课程教学课件(PPT讲稿)例3-7-9(频域微分).ppt
- 《信号与系统》课程教学课件(PPT讲稿)§3.8 卷积特性(卷积定理).ppt
- 《信号与系统》课程教学课件(PPT讲稿)时域卷积定理证明.ppt
- 《信号与系统》课程教学课件(PPT讲稿)§3.9 周期信号的傅里叶变换.ppt
