西安电子科技大学：《神经网络与模糊系统 Neural Networks and Fuzzy Systems》课程PPT课件讲稿（2006）Chapter 03-2 NEURONAL DYNAMICS 2：ACTIVATION MODELS

Bivalent BAM theorem -The average signal energy L of the forward pass of theFx Signal state vector S(X)through M,and the backward pass Of the Fy signal state vectorS(Y)through M?: L=一 S(X)MS(Y)+S(Y)M'S(X) 2 since S(M'S(X)=[S(MS(X) =S(X)MS(Y) L=-SX)MSY)y=-∑∑S(x,)S,Oy,m 2

2 Bivalent BAM theorem The average signal energy L of the forward pass of the Signal state vector through M,and the backward pass Of the signal state vector through : FX S(X) T FY S(Y) M 2 ( ) ( ) ( ) ( ) T T T S X MS Y S Y M S X L + = − T T T T T S(Y)M S(X) =[S(Y)M S(X) ] T = S(X)MS(Y) since T L = −S(X)MS(Y) i j n i p j = −Si (xi )S j ( y j )m

Lower bound of Lyapunov function -The signal energy Lyapunov function is clearly bounded below. For binary or bipolar,the matrix coefficients define the attainable bound:L≥-∑∑m,l i -The attainable upper bound is the negative of this expression. 3

3 Lower bound of Lyapunov function The signal energy Lyapunov function is clearly bounded below. For binary or bipolar,the matrix coefficients define the attainable bound: The attainable upper bound is the negative of this expression.  − i j L mij

Lyapunov function for the general BAM system -The signal-energy Lyapunov function for the general BAM system takes the form L=-S(X)MS(Y)"-S(X)I-U-S(Y)J- Inputs I=[i,…,Iv]andJ=[Ui,…,Jp]and constant vectors of thresholds U=[U,,Ux]V=[V,,V] the attainable bound of this function is. ≥∑∑m∑-l-∑，-h 4

4 Lyapunov function for the general BAM system The signal-energy Lyapunov function for the general BAM system takes the form Inputs and and constant vectors of thresholds the attainable bound of this function is. T T T L = −S(X)MS(Y) − S(X) [I −U] − S(Y) [J −V] [ , , ] N I I  I = 1 [ , , ] P J J  J = 1 [ , , ] U U1  UN = [ , , ] V V1  VN =  − − − − − j j j i i i i j L mi j [ I U ] [ J V ]

Bivalent BAM theorem -Bivalent BAM theorem:every matrix is bidirectionally stable for synchronous or asynchronous state changes. Proof:consider the signal state changes that occur from time k to time k+1,define the vectors of signal state changes as: △S(X)=S(Xk+1)-S(Xk) =(AS(x)2…,ASn(xn),) AS(Y)=S(Y)-S(Y) =AS(y)2…,S,yp),） 5

5 Bivalent BAM theorem Bivalent BAM theorem: every matrix is bidirectionally stable for synchronous or asynchronous state changes. Proof: consider the signal state changes that occur from time k to time k+1,define the vectors of signal state changes as: ( ( ), , ( ),) ( ) ( ) ( ) 1 1 1 n n k k S x S x S X S X S X =    = + −  ( ( ), , ( ),) ( ) ( ) ( ) 1 1 1 p p k k S y S y S Y S Y S Y =    = + − 

Bivalent BAM theorem -define the individual state changes as: △S,(x)=S,(x,+l)-S,(x;) AS,(y,）=S,y,)-S,(y,) -We assume at least one neuron changes state from k to time k+1. Any subset of neurons in a field can change state,but in only one field at a time. For binary threshold signal functions if a state change is nonzero, 6

6 Bivalent BAM theorem define the individual state changes as: ( ) ( ) ( ) k i i k i i i i S x = S x − S x +1 ( ) ( ) ( ) k j j k j j j j S y = S y − S y +1 We assume at least one neuron changes state from k to time k+1. Any subset of neurons in a field can change state,but in only one field at a time. For binary threshold signal functions if a state change is nonzero

Bivalent BAM theorem △S,(x)=1-0=1△S,(x;)=0-1=-1 For bipolar threshold signal functions AS,(x)=2 AS,(x;)=-2 The“energy'change△L △L=Lk+1-Lk Differs from zero because of changes in field Fy or in field Fy 7

7 Bivalent BAM theorem Si (xi ) = 1− 0 = 1  ( ) = 0 −1 = −1 i i S x Si (xi ) = 2 Si (xi ) = −2 For bipolar threshold signal functions The “energy”change L L = Lk+1 − Lk Differs from zero because of changes in field or in field FX FY

Bivalent BAM theorem △L=-△S(X)MS(Yk)'-△S(X)[I-U] =-AS(X)IS(Y)M-U =-∑∑AS,(,)S,0y)m∑AS,(x)山，+∑AS,(x,U -∑As,(G∑S0ym,-∑aSx川，+∑As, =-∑AS,(x)∑S,)m,+1,-U] =-AS,(x,Ix41-U月 8

8 Bivalent BAM theorem T T L = −S(X)MS(Yk ) − S(X) [I −U] T T = −S(X)[S(Yk )M −[I −U]] = − − + i i i i i i i i i j i j k T Si xi S j y m S x I S x U j ( ) ( ) ( ) ( ) = −  − + i i i i i i i i i j i j k T Si xi S j y m S x I S x U j ( ) ( ) ( ) ( ) ( )[ ( ) ] i i i j i j k T Si xi S j y m I U j = −  + − ( )[ ]i i k = −Si xi xi −U +1  0

Bivalent BAM theorem Suppose AS;(x;)>0 Then AS;(x)=S;()-S;(x) =1-0 This implies so the product is positive: △S,(x,)[x+1-U,]>0 Another case suppose AS;(x;)<0 △S,(x)=S,(x,k+1)-S,(x,) =0-1 9

9 Bivalent BAM theorem Suppose Si (xi )  0 ( ) ( ) ( ) k i i k i i i i S x = S x − S x +1 = 1− 0 Then This implies so the product is positive: i k xi U +1 0 1  −  + ( )[ ] i k Si xi xi U Another case suppose Si (xi )  0 ( ) ( ) ( ) k i i k i i i i S x = S x − S x +1 = 0 −1

Bivalent BAM theorem -This impliesxUs so the product is positive: AS,(x)[x+1-U,>0 So+-Lk<0 for every state change. -Since L is bounded,L behaves as a Lyapunov function for the additive BAM dynamical system defined by before. Since the matrix M was arbitrary,every matrix is bidirectionally stable.The bivalent BAM theorem is proved. 10

10 Bivalent BAM theorem This implies so the product is positive: i k xi U +1 0 1  −  + ( )[ ] i k Si xi xi U So for every state change. 0 Lk+1 − Lk  Since L is bounded,L behaves as a Lyapunov function for the additive BAM dynamical system defined by before. Since the matrix M was arbitrary,every matrix is bidirectionally stable. The bivalent BAM theorem is proved

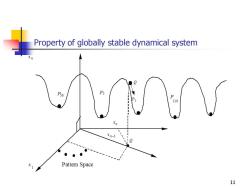
Property of globally stable dynamical system 56 P2 110 Xn-1 Pattern Space 11

11 Property of globally stable dynamical system