南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Rounding Linear Program

Advanced Algorithms Rounding Linear Program 尹一通Nanjing University,2022Fall
尹⼀通 Nanjing University, 2022 Fall Advanced Algorithms Rounding Linear Program

Vertex Cover
Vertex Cover
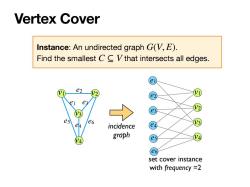
Vertex Cover Instance:An undirected graph G(V,E). Find the smallest C V that intersects all edges. e2 e es e6 incidence graph V4 V4 set cover instance with frequency =2
Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V v1 v2 v3 v4 e1 e3 e2 e4 e1 e2 e3 e4 v1 v2 v3 e5 v4 e6 incidence graph set cover instance with frequency =2 e5 e6

Vertex Cover Instance:An undirected graph G(V,E). Find the smallest C V that intersects all edges. ·NP-hard In(n)-approximation by greedy set cover 2-approximation algorithm: Find a maximal matching; return the matched vertices; .[Khot,Regev 2008]Assuming the unique games conjecture, there is no poly-time(2-e)-approximation algorithm
• NP-hard • -approximation by greedy set cover • 2-approximation algorithm: • [Khot, Regev 2008] Assuming the unique games conjecture, there is no poly-time -approximation algorithm. ln(n) (2 − ϵ) Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V Find a maximal matching; return the matched vertices;
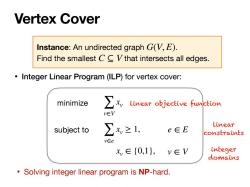
Vertex Cover Instance:An undirected graph G(V,E). Find the smallest CC Vthat intersects all edges. Integer Linear Program(ILP)for vertex cover: minimize ∑x linear objective function v∈V subject to ∑x≥1, Linear e∈E constraints v∈e x,∈{0,1},v∈V integer domains Solving integer linear program is NP-hard
• Integer Linear Program (ILP) for vertex cover: Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V minimize subject to ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E v ∈ V linear objective function linear constraints integer domains • Solving integer linear program is NP-hard

Vertex Cover Instance:An undirected graph G(V,E). Find the smallest C Vthat intersects all edges. Linear Program(LP)relaxation: minimize ∑x v∈V subject to ∑x≥1, e∈E v∈e x∈[0,1], v∈V fractional domains linear programs are solvable in polynomial time!
• Linear Program (LP) relaxation: Vertex Cover Instance: An undirected graph . Find the smallest that intersects all edges. G(V, E) C ⊆ V minimize subject to ∑ v∈V xv ∑ v∈e xv ≥ 1, xv ∈ {0,1}, e ∈ E v ∈ V • linear programs are solvable in polynomial time! [ ] fractional domains

Linear Programming (LP) ·General form: matrix A={dijmxin],sets M [ml and NS [n] minimize cTx subject to afx =bi i∈M a,x≥b i∈M 光≥0 j∈N x;unconstrained j∈N
• General form: • matrix A = {a , sets and ij }[m]×[n] M ⊆ [m] N ⊆ [n] Linear Programming (LP) minimize subject to cTx aT i x = bi aT i x ≥ bi xj ≥ 0 xj unconstrained i ∈ M i ∈ M j ∈ N j ∈ N
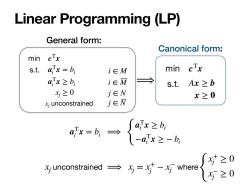
Linear Programming (LP) General form: Canonical form: min cTx s.t. ajx=b i∈M min cTx ax≥b, i∈M → s.t.Ax≥b 为≥0 j∈N x≥0 x;unconstrained j∈N -6-{的0 x;unconstrained→ 5咖e0 (七≥0
Linear Programming (LP) min s.t. cTx aT i x = bi aT i x ≥ bi xj ≥ 0 xj unconstrained i ∈ M i ∈ M j ∈ N j ∈ N General form: Canonical form: aT i x = bi ⟹ { aT i x ≥ bi −aT i x ≥ − bi x where j unconstrained ⟹ xj = x+ j − x− j { x+ j ≥ 0 x− j ≥ 0 ⟹ min s.t. cTx Ax ≥ b x ≥ 0

Convex Polytopes 。hyperplane: subspace of dimension n-1 ∑a45=b j=1 (closed,affine)halfspace: ∑a4y≥b j=1 。convex polyhedron: intersection of finitely many halfspaces convex polytope:bounded convex polyhedron
• hyperplane: subspace of dimension • (closed, affine) halfspace: • convex polyhedron: intersection of finitely many halfspaces • convex polytope: bounded convex polyhedron n − 1 n ∑ j=1 ajxj = b n ∑ j=1 ajxj ≥ b Convex Polytopes
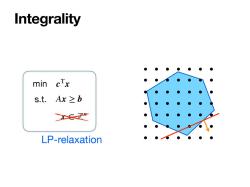
Integrality min cTx s.t.Ax≥b Z LP-relaxation
x ∈ ℤn Integrality min s.t. cTx Ax ≥ b LP-relaxation
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)LP Duality.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Dimension Reduction.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Rounding Data.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Lovász Local Lemma.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Hashing and Sketching.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Greedy and Local Search.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Fingerprinting.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Introduction(Min-Cut and Max-Cut,尹⼀通).pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Concentration of Measure.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Balls into Bins.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Greedy and Local Search.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Fingerprinting.pdf
- 电子科技大学:《有限元理论与建模方法 Finite Element Analysis and Modeling》研究生课程教学资源(课件讲稿)第二篇 有限元建模方法 第十八章 边界条件的建立 Creation of Boundary Condition.pdf
- 电子科技大学:《有限元理论与建模方法 Finite Element Analysis and Modeling》研究生课程教学资源(课件讲稿)第二篇 有限元建模方法 第十七章 模型检查与处理 Model Checking and Processing.pdf
- 电子科技大学:《有限元理论与建模方法 Finite Element Analysis and Modeling》研究生课程教学资源(课件讲稿)第二篇 有限元建模方法 第十六章 网格划分方法.pdf
- 电子科技大学:《有限元理论与建模方法 Finite Element Analysis and Modeling》研究生课程教学资源(课件讲稿)第二篇 有限元建模方法 第十五章 单元类型及特性定义.pdf
- 电子科技大学:《有限元理论与建模方法 Finite Element Analysis and Modeling》研究生课程教学资源(课件讲稿)第二篇 有限元建模方法 第十四章 几何模型的建立.pdf
- 电子科技大学:《有限元理论与建模方法 Finite Element Analysis and Modeling》研究生课程教学资源(课件讲稿)第二篇 有限元建模方法 第十一章 有限元建模的基本原则.pdf
- 电子科技大学:《有限元理论与建模方法 Finite Element Analysis and Modeling》研究生课程教学资源(课件讲稿)第二篇 有限元建模方法 第十二章 有限元建模概述 Overview of Finite Element Modeling.pdf
- 电子科技大学:《有限元理论与建模方法 Finite Element Analysis and Modeling》研究生课程教学资源(课件讲稿)第八章 热分析有限元法 FEM of Thermal Analysis.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)SDP-Based Algorithms.pdf
- 南京大学:《高级算法 Advanced Algorithms》课程教学资源(课件讲稿)Exercise Lecture For Advanced Algorithms(2022 Fall).pdf
- 南京大学:《组合数学 Combinatorics》课程教学资源(课件讲稿)Basic Enumeration(主讲:尹一通).pdf
- 南京大学:《组合数学 Combinatorics》课程教学资源(课件讲稿)Cayley.pdf
- 南京大学:《组合数学 Combinatorics》课程教学资源(课件讲稿)Existence.pdf
- 南京大学:《组合数学 Combinatorics》课程教学资源(课件讲稿)Extremal Combinatorics.pdf
- 南京大学:《组合数学 Combinatorics》课程教学资源(课件讲稿)Extremal Sets.pdf
- 南京大学:《组合数学 Combinatorics》课程教学资源(课件讲稿)Generating Function.pdf
- 南京大学:《组合数学 Combinatorics》课程教学资源(课件讲稿)Matching Theory.pdf
- 南京大学:《组合数学 Combinatorics》课程教学资源(课件讲稿)Polya.pdf
- 南京大学:《组合数学 Combinatorics》课程教学资源(课件讲稿)Principle of Inclusion-Exclusion(PIE).pdf
- 南京大学:《组合数学 Combinatorics》课程教学资源(课件讲稿)The Probabilistic Method.pdf
- 南京大学:《组合数学 Combinatorics》课程教学资源(课件讲稿)Ramsey Theory.pdf
- 南京大学:《随机算法 Randomized Algorithms》课程教学资源(课件讲稿)Balls and Bins.pdf
- 南京大学:《随机算法 Randomized Algorithms》课程教学资源(课件讲稿)Chernoff.pdf
- 南京大学:《随机算法 Randomized Algorithms》课程教学资源(课件讲稿)Concentration.pdf
- 南京大学:《随机算法 Randomized Algorithms》课程教学资源(课件讲稿)Coupling.pdf
- 南京大学:《随机算法 Randomized Algorithms》课程教学资源(课件讲稿)Finger printing.pdf
- 南京大学:《随机算法 Randomized Algorithms》课程教学资源(课件讲稿)Identity Testing.pdf
- 南京大学:《随机算法 Randomized Algorithms》课程教学资源(课件讲稿)Lovász Local Lemma.pdf
