南京大学：《高级算法 Advanced Algorithms》课程教学资源（课件讲稿）Fingerprinting

Advanced Algorithms Fingerprinting 尹一通Nanjing University,2021Fall

尹⼀通 Nanjing University, 2021 Fall Advanced Algorithms Fingerprinting

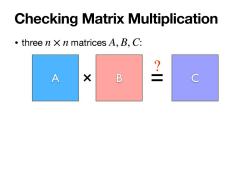
Checking Matrix Multiplication three n x n matrices A,B,C: A X B 是 C

• three n × n matrices A, B,C: Checking Matrix Multiplication A × B = C ?

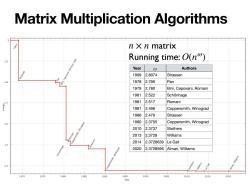
Matrix Multiplication Algorithms n Xn matrix Running time:O(n) 2.9 Year 0 Authors Strassen apovani,Romani,Lotti 1969 2.8074 Strassen 28 1978 2.796 Pan 1979 2.780 Bini,Capovani,Romani 1981 2.522 Schonhage 1981 2.517 Romani 1981 2.496 Coppersmith,Winograd 1986 2.479 Strassen ■g年市n车a年 1990 2.3755 26 Coppersmith,Winograd 2010 2.3737 Stothers Romani smith, 2013 2.3729 Williams Copp ssen 2014 2.3728639 Le Gall 2.5 age 2020 2.3728596 Alman,Williams 2.4 Coppersmith.Winograd 1970 1975 1980 1985 1990 1995 2000 2005 2010 2015 2020 Year

Matrix Multiplication Algorithms matrix Running time: n × n O(nω) Year ω Authors 1969 2.8074 Strassen 1978 2.796 Pan 1979 2.780 Bini, Capovani, Romani 1981 2.522 Schönhage 1981 2.517 Romani 1981 2.496 Coppersmith, Winograd 1986 2.479 Strassen 1990 2.3755 Coppersmith, Winograd 2010 2.3737 Stothers 2013 2.3729 Williams 2014 2.3728639 Le Gall 2020 2.3728596 Alman, Williams

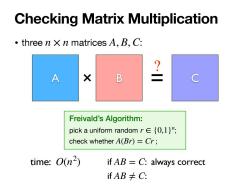
Checking Matrix Multiplication three n xn matrices A,B,C: A X B 名 C Freivald's Algorithm: pick a uniform random r∈{0，l}n; check whether A(Br)=Cr; time:O(n2) if AB C:always correct ifAB≠C:

• three n × n matrices A, B,C: Checking Matrix Multiplication A × B = C ? Freivald’s Algorithm: pick a uniform random ; check whether ; r ∈ {0,1}n A(Br) = Cr time: O(n if AB = C: always correct 2 ) if AB ≠ C:

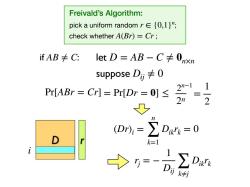
Freivald's Algorithm: pick a uniform random r∈{0，l}, check whether A(Br)=Cr; fAB≠C: letD=AB-C卡0xn suppose Dii卡0 1 Pr[ABr =Cr]=Pr[Dr=0]< 三 2 (Dr,=∑D4=0 D r k=1 i 之2

Freivald’s Algorithm: pick a uniform random ; check whether ; r ∈ {0,1}n A(Br) = Cr if AB ≠ C: let D = AB − C ≠ 0n×n D r i suppose Dij ≠ 0 Pr[ABr = Cr] = Pr[Dr = 0] ≤ (Dr)i = n ∑ k=1 Dikrk = 0 rj = − 1 Dij ∑ k≠j Dikrk = 1 2 2 n 2n−1

Freivald's Algorithm: pick a uniform random r∈{0，l}, check whether A(Br)=Cr; if AB C:always correct Theorem(Feivald 1979). For n X n matrices A,B,C,ifAB≠C,for uniform random r∈{0，l}n, Pr[ABr=C1≤2 repeat independently for O(log n)times Total running time:O(n2log n) Correct with high probability (w.h.p.)

Freivald’s Algorithm: pick a uniform random ; check whether ; r ∈ {0,1}n A(Br) = Cr Theorem (Feivald 1979). For n × n matrices A, B,C, if AB ≠ C, for uniform random r ∈ {0,1} , n Pr[ABr = Cr] ≤ 1 2 if AB = C: always correct repeat independently for O(log n) times Total running time: Correct with high probability (w.h.p.). O(n2 log n)

Polynomial Identity Testing (PIT) Input:two polynomials fg E Fx]of degree d. Output:f三g? Fx]:polynomial ring in x over field F f∈rL]of degree d:f)=∑a where a,∈F =0 field Input:a polynomial fE Fx]of degree d. Output:f三0？ fis given as black-box

Polynomial Identity Testing (PIT) Input: two polynomials of degree . Output: ? f, g ∈ 𝔽[x] d f ≡ g Input: a polynomial of degree . Output: ? f ∈ 𝔽[x] d f ≡ 0 f ∈ 𝔽[x] of degree d: f(x) = where d ∑ i=0 ai xi ai ∈ 𝔽 f is given as black-box field 𝔽[x]: polynomial ring in x over field 𝔽

Input:a polynomial fE Fx]of degree d. Output:f三0？ Deterministic algorithm (polynomial interpolation): pick arbitrary distinct., check if f(x)=0 for all0≤i≤d; Fundamental Theorem of Algebra. Any non-zero d-degree polynomial fE Fx]has at most d roots. Randomized algorithm(fingerprinting): pick a uniform random re S; let S Fbe arbitrary check if f(r)=0; (whose size to be fixed later)

Input: a polynomial of degree . Output: ? f ∈ 𝔽[x] d f ≡ 0 • Deterministic algorithm (polynomial interpolation): pick arbitrary distinct ; check if for all ; x0, x1, …, xd ∈ 𝔽 f(xi ) = 0 0 ≤ i ≤ d • Randomized algorithm (fingerprinting): pick a uniform random ; check if ; r f(r) = 0 ∈ S let be arbitrary (whose size to be fixed later) S ⊆ 𝔽 Fundamental Theorem of Algebra. Any non-zero d-degree polynomial f ∈ 𝔽[x] has at most d roots

Input:a polynomial fE Fx]of degree d. Output:f三0？ pick a uniform random re S; let S Fbe arbitrary check if f(r)=0; (whose size to-be fixed later) |S|=2d iff≡O:always correct ff丰0： Pr[fr）=O]≤ d 1 ISI 2 Fundamental Theorem of Algebra. Any non-zero d-degree polynomial f Fx]has at most d roots

pick a uniform random ; check if ; r f(r) = 0 ∈ S let be arbitrary (whose size to be fixed later) S ⊆ 𝔽 if f ≡ 0: always correct Input: a polynomial of degree . Output: ? f ∈ 𝔽[x] d f ≡ 0 if f ≢ 0: Pr[f(r) = 0] ≤ |S| Fundamental Theorem of Algebra. Any non-zero d-degree polynomial f ∈ 𝔽[x] has at most d roots. d |S| = 2d = 1 2

Checking Identity 北京 database 1 Are they identical? 南京 database 2

Checking Identity database 1 database 2 Are they identical? 北京 南京