西华大学：《统计学》课程教学课件（PPT讲稿）第5章 动态分析法

第五章 动态分析法 第一节时间数列 意义 种类：总量、相对、平均数列 ◆三、编制时间数列的原则： 1、指标所属的时间的可比性； ◆2、总体范围的前后一致； 兼3、计算的口径方法的可比性： 兼4、经济内容的可比性

第五章 动态分析法  第一节 时间数列 一、意义 二、种类：总量、相对、平均数列 三、编制时间数列的原则：  1、指标所属的时间的可比性；  2、总体范围的前后一致；  3、计算的口径方法的可比性；  4、经济内容的可比性

第二节指标分析法 、 动态水平法： 1、发展水平：在一定时间社会经济现象发 展达到的水平。 ◆注：可以是总量、相对、平均水平： ◆表达：a0a1a2a3。an时 ◆在对比中：a0a1a2a3。an-1 基期水平 a,a2a3。.an-1an_报告期水平 兼2、平均发展水平： 兼①总量数列：

第二节 指标分析法 一、动态水平法：  1、发展水平：在一定时间社会经济现象发 展达到的水平。 注：可以是总量、相对、平均水平； 表达：a0 a1 a2 a3 。 an； 在对比中： a0 a1 a2 a3 。 an-1-基期水平  a1 a2 a3 。 an-1 an-报告期水平  2、平均发展水平： ①总量数列：

兼A、 时期数列：a1a2a3。.an a=∑a,/n B、时点数列： 简单：a=∑a/n ◆连续时点数列：{ 加权：a=∑af/∑f ◆间断时点数列（等间隔）： ◆a1a2ag。 。 an ◆a=ha1+a2+.2an/n-1 ◆②相对数列（平均数列）：c=ab c=a/b

 A、时期数列： a1 a2 a3 。 an  ā=∑ai /n  B、时点数列：  简单：ā=∑ai /n 连续时点数列：{  加权：ā=∑ai f i / ∑fi 间断时点数列（等间隔）：  a1 a2 a3 。 an  ā=½ a1 + a2 +.½an /n-1 ②相对数列（平均数列）：c=a/b  ĉ=ā/b¯

A、子、母项都为时期指标： c=∑a,/∑b ◆B、子、母项分别为时期、时点指标： 如 c=∑a/n 2b1+b2.+2bm/m-1 C、 子母项都为时点指标： Vata.+veanin-1 c= 2b,+b2.+½b/n-1

 A、子、母项都为时期指标：  ĉ= ∑ai / ∑bi  B、子、母项分别为时期、时点指标： 如 ĉ= ∑ai / n  ½b1+b2.+ ½bm/m-1  C、子母项都为时点指标：  ½a1+a2.+ ½an /n-1  ĉ=  ½b1+b2.+ ½bn /n-1

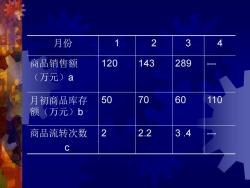
月份 1 2 3 4 商品销售额 120 143 289 (万元)a 月初商品库存 50 70 60 110 额（万元）b 商品流转次数 2 2.2 3.4 c

月份 1 2 3 4 商品销售额 （万元）a 120 143 289 - 月初商品库存 额（万元）b 50 70 60 110 商品流转次数 c 2 2.2 3 .4 -

c=∑a/n ½b1tb2.+½bm/m-1 =120+143+289/3 250+70+60+2110/4-1 =2.63 ◆3、增减量和平均增减量水平 1) 增减量=a报~a基 逐期增减量=a-a1=1,2,.n 累计增长量=a-ao j=1,2,.n 关系：a-a=∑（a-a1) 2) 平均增减量=∑(a-a1)n 举二、 速度分析： 兼1、 发展速度=a报a基

 ĉ= ∑ai / n  ½b1+b2.+ ½bm/m-1  =120+143+289/3  ½50+70+60+ ½110/4-1  =2.63  3、增减量和平均增减量水平  1）增减量= a报- a基  逐期增减量= ai - ai-1 i=1，2,.n  累计增长量=ai - a0 i=1，2,.n  关系： ai - a0 = ∑ （ai - ai-1 ）  2）平均增减量= ∑ （ai - ai-1 ）/n  二、速度分析：  1、发展速度= a报/ a基

环比发展速度=a,/a.1=1,2,n 定基发展速度=a,/a0=1,2,.n ◆二者关系：a/ao=几a/a-1=R ·2、增减速度=发展速度-100% ◆环比增减速度=a/a1-1 定基增减速度=a/a,1 ◆3、平均速度： ◆1)平均发展速度： 兼A、水平法 ◆X=(a,/ao) 1n= (Πa,/a-1)1n=R1n 兼B、方程式法 a+a2+an=∑a→X+X1+X2.+Xn=∑a/n

 环比发展速度=ai / ai-1 i=1，2,.n  定基发展速度=ai / a0 i=1，2,.n  二者关系： ai / a0 = ∏ai / ai-1 =R  2、增减速度=发展速度-100%  环比增减速度= ai / ai-1 –1  定基增减速度= ai / a0 - 1  3、平均速度：  1）平均发展速度：  A、水平法  X=（ai / a0）1/n = （∏ai / ai-1 ） 1/n =R 1/n  B、方程式法  a1+a2.+ an= ∑ai→X+X1+X2.+Xn= ∑ai /n

◆2)平均增长速度 兼4、应用平均速度应注意的问题 ◆A、平均速度要和环比速度结合分析； B、总平均速度要和段平均速度结合分析 C、平均速度要联系基期水平进行分析

 2）平均增长速度  4、应用平均速度应注意的问题  A、平均速度要和环比速度结合分析；  B、总平均速度要和段平均速度结合分析 C、平均速度要联系基期水平进行分析

第三节成分分析法 一、时间数列的成分与组合： 1、 成分：T、C、S、I ◆2、模型： ◆加法模型：Y=T+C+S+: ◆乘法模型：Y=T*C*S*I; ◆混合模型：Y=T*C+S*I等。 兼二、长期趋势的测定和分析： 兼1、移动平均法： 兼A、方法过程：

第三节 成分分析法 一、时间数列的成分与组合：  1、成分：T、C、S、I  2、模型： 加法模型：Y=T+C+S+I； 乘法模型：Y=T*C*S*I； 混合模型：Y=T*C+S*I等。 二、长期趋势的测定和分析：  1、移动平均法：  A、方法过程：

1)n为奇：以n=3为例： 兼2)n为偶：l 以n=4为例： a n=3 n=4 移正 2 a1+a2+a3/3 a1+a2+a3+a4/4 83 a2ta3+a,/3 一半 a2ta3+a4+a5/4 a4a3+a4+a5/3 a5

 1）n为奇：以n=3为例；  2）n为偶：以n=4为例。  a n=3 n=4 移正  a1 - -   a2 a1+a2+a3 /3 -  a1+a2+a3 +a4 /4  a3 a2+a3 +a4 /3 } 一半  a2+a3 +a4+ a5 /4  a4 a3 +a4 +a5 /3  a5 -