福州大学：《统计学》课程教学资源（课件讲稿）第九章 方差分析

第九章方差分析

第九章 方差分析

第九章方差分析 学习目标： 1、理解方差分析的基本思想； 2、熟练掌握单因素方差分析的基本原理及其 实际应用； 3、熟练掌握双因素方差分析的基本原理及其 实际应用

第九章 方差分析 学习目标: 1、理解方差分析的基本思想； 2、熟练掌握单因素方差分析的基本原理及其 实际应用； 3、熟练掌握双因素方差分析的基本原理及其 实际应用

9.1方差分析的基本认识 9.1.1 问题的提出 9.1.2 方差分析的基本概念

9.1 方差分析的基本认识 9.1.1 问题的提出 9.1.2 方差分析的基本概念

9.1.1问题的提出 方差分析是对多个总体均值是否相等这一假设进 行检验。 [例9-1]某化妆品生产公司研制出一种新型爽肤 水。爽肤水的颜色共有四种，分别为橘黄色、粉色、 绿色和无色透明。现随机从五家专卖市场上收集了前 期该种爽肤水的销售量，如表9一1所示。 问爽肤水的颜色是否对销售量产生影响

9.1.1 问题的提出 方差分析是对多个总体均值是否相等这一假设进 行检验。 [例9-1]某化妆品生产公司研制出一种新型爽肤 水。爽肤水的颜色共有四种，分别为橘黄色、粉色、 绿色和无色透明。现随机从五家专卖市场上收集了前 一期该种爽肤水的销售量，如表9－1所示。 问爽肤水的颜色是否对销售量产生影响

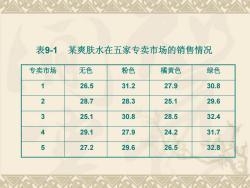
表9-1某爽肤水在五家专卖市场的销售情况 专卖市场 无色 粉色 橘黄色 绿色 26.5 31.2 27.9 30.8 2 28.7 28.3 25.1 29.6 3 25.1 30.8 28.5 32.4 4 29.1 27.9 24.2 31.7 5 27.2 29.6 26.5 32.8

表9-1 某爽肤水在五家专卖市场的销售情况 专卖市场 无色 粉色 橘黄色 绿色 1 26.5 31.2 27.9 30.8 2 28.7 28.3 25.1 29.6 3 25.1 30.8 28.5 32.4 4 29.1 27.9 24.2 31.7 5 27.2 29.6 26.5 32.8

这是一个方差分析问题，即对四种不同颜色的爽肤 水的销售量均值是否相等进行检验。 把四种不同颜色的爽肤水的销售量均值分别记为 4,2,43,44 由题意知，要检验假设H。:4=山2=4=44 H1:H1,2,3,4不全相等 如果检验结果为不全相等，则表明爽肤水颜色对销 售量产生影响。反之，如果检验结果为不存在显著影 响，则可以认为爽肤水颜色对销售量没有影响，他们来 自于相同的总体

这是一个方差分析问题，即对四种不同颜色的爽肤 水的销售量均值是否相等进行检验。 把四种不同颜色的爽肤水的销售量均值分别记为 由题意知，要检验假设 不全相等 如果检验结果为不全相等，则表明爽肤水颜色对销 售量产生影响。反之，如果检验结果为不存在显著影 响，则可以认为爽肤水颜色对销售量没有影响，他们来 自于相同的总体。 1234 μ , μμμ 01 2 3 4 H : μ = μμμ = = 1 1234 H :, μ μμμ

9.1.1问题的提出 方差分析简称ANOVA(analysis of variance),就是 利用试验观测值总偏差的可分解性，将不同条件所引起的 偏差与随机误差分解开来，按照一定的规则进行比较，以 确定各种偏差的影响程度和相对大小.当已确定某几种因 素对试验结果有显著影响时，可使用方差分析检验确定哪 种因素对试验结果的影响最为显著及估计影响程度

9.1.1 问题的提出 方差分析简称ANOVA(analysis of variance)，就是 利用试验观测值总偏差的可分解性，将不同条件所引起的 偏差与随机误差分解开来，按照一定的规则进行比较，以 确定各种偏差的影响程度和相对大小. 当已确定某几种因 素对试验结果有显著影响时，可使用方差分析检验确定哪 种因素对试验结果的影响最为显著及估计影响程度

9.1.2方差分析的基本概念 我们把要考察的对象的某种特征称为指标。试验条件 分为可控制的和不可控制的两类，称可控制的试验条件为 因素；因素所处的状态称为该因素的水平。如果在一项试 验中只有一个因素在变化，称他为单因素试验。若试验中 变化因素多于一个，称他为双因素以及多因素试验。在例 9-1中，爽肤水的销售量为指标，爽肤水的颜色为因素， 爽肤水的四种颜色为该因素的四个水平，该例是一个单因 素四水平试验。假设检验章所讲的对两个总体均值的比 较，实际上就是单因素两水平试验

9.1.2 方差分析的基本概念 我们把要考察的对象的某种特征称为指标。试验条件 分为可控制的和不可控制的两类，称可控制的试验条件为 因素；因素所处的状态称为该因素的水平。如果在一项试 验中只有一个因素在变化，称他为单因素试验。若试验中 变化因素多于一个，称他为双因素以及多因素试验。在例 9-1中，爽肤水的销售量为指标，爽肤水的颜色为因素， 爽肤水的四种颜色为该因素的四个水平，该例是一个单因 素四水平试验。假设检验章所讲的对两个总体均值的比 较，实际上就是单因素两水平试验

9.2单因素方差分析 9.2.1单因素方差分析的基本原理 9.2.2单因素方差分析应用实例 9.2.3单因素方差分析中应注意的问题

9.2 单因素方差分析 9.2.1 单因素方差分析的基本原理 9.2.2 单因素方差分析应用实例 9.2.3 单因素方差分析中应注意的问题

9.2.1单因素方差分析的基本原理 单因素方差分析是研究一个因素的变化对试验指标的影响 是否显著的统计分析方法。 设因素A有个水平A,A,: A 在水平4(i=1,2,.,r)下 进行n,(≥2)次独立试验，锰验记绿如表9-2 表9-2独立试验记录表 样本 水平 n 4 古 X :4 :

9.2.1 单因素方差分析的基本原理 单因素方差分析是研究一个因素的变化对试验指标的影响 是否显著的统计分析方法。 设因素A有r个水平 在水平 下 进行 次独立试验，试验记录如表9-2 表 9-2 独立试验记录表 1 2 , A A A L r Ai ( 1, 2, , ) i r = L ( 2) i n i ≥ 1 L j L i n A1 M Ai M A r X11 X1 j L L 1 X1n M M M Xi1 L L Xij i Xin M M M X r1 Xrj L L r X rn 样本 水平