河套学院（河套大学）：《线性代数》课程教学资源（PPT课件讲稿）第二章 矩阵 2.3 逆矩阵（2/2）

第二章 矩阵 目录 四 2.1 矩阵的概念 四 2.2 矩阵的运算 2.3 逆矩阵(2) 四 2.4 矩阵的分块 四 2.5 初等变换与初等矩阵 四 2.6 矩阵的秩 四 2.7 应用举例 河套大学《线性代数》课件 第二章矩阵 快乐学司

第二章 矩 阵  2.1 矩阵的概念  2.2 矩阵的运算 ★ 2.3 逆矩阵(2)  2.4 矩阵的分块  2.5 初等变换与初等矩阵  2.6 矩阵的秩  2.7 应用举例 目录 河套大学《线性代数》课件 第二章 矩阵 快乐学习

本节授裸计划 水人 (2课时) 苟本 必复习 新课2.3 逆矩阵(2) 第十二次 2.3.3 可逆矩阵的性质 必小结 必思考题及答案提示 练习、作业及参考答案 河套大学《线性代数》课件 第二章矩阵 快乐学司

快乐学习 以人 为本 ❖复习 ❖新课 2.3 逆矩阵(2) 2.3.3 可逆矩阵的性质 ❖小结 ❖思考题及答案提示 ❖练习、作业及参考答案 第 十 二 次 课 本节授课计划（2课时） 河套大学《线性代数》课件 第二章 矩阵

水人 2.3.3 可逆矩阵的性质 尚本 主题调 穿脱原理 可逆矩阵 的性质 返回 河套大学《线性代数》课件 第二章矩阵 快东学司

快乐学习 以人 为本 主 题 词 2.3.3 可逆矩阵的性质 河套大学《线性代数》课件 第二章 矩阵 1、穿脱原理 2、可逆矩阵 的性质 返回

相关内容回顺1 水人 尚本 逆矩阵的概念及其推论、可逆的充要条件 对于n阶矩阵A,若有一个n阶矩阵B,使得 AB=BA=E. 则称矩阵A为可逆矩阵（或称矩阵A可逆）， 而矩阵B称为A的逆矩阵 递矩阵 的桡念 河套大学《线性代数》课件 第二章矩阵 快乐骨司

，若有一个 阶矩阵 使得 为可逆矩阵（或 称矩阵 可逆）， 逆矩阵的概念及其推论、可逆的充要条件 快乐学习 以人 相关内容回顾 1 为本 河套大学《线性代数》课件 第二章 矩阵 逆矩阵 的概念 n 阶矩阵 A n B, AB = BA = E, 对于 A A B A 则称矩阵 而矩阵 称为 的逆矩阵

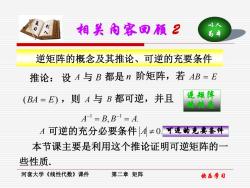
相关内容国预2 水人 尚本 逆矩阵的概念及其推论、可逆的充要条件 推论：设A与B都是n阶矩阵，若AB=E （BA=E),则A与B都可逆，并且 遂矩阵 的性项 4=BB=A A可逆的充分必要条件A≠0， 可递的充要条件 本节课主要是利用这个推论证明可逆矩阵的 些性质 河套大学《线性代数》课件 第二章矩阵 快东学司

逆矩阵的概念及其推论、可逆的充要条件 快乐学习 以人 相关内容回顾 2 为本 河套大学《线性代数》课件 第二章 矩阵 逆矩阵 的性质 A B n AB = E (BA = E) A B , . 1 1 A = B B = A − − 推论： 设 与 都是 阶矩阵，若 ，则 与 都可逆，并且 本节课主要是利用这个推论证明可逆矩阵的一 些性质. A 可逆的充分必要条件 A  0. 可逆的充要条件

水人 2.3.3可逆矩阵的性质 尚本 性质2.3.1若 A可逆，则A也可逆，且 (A)=A,A 证明由AA=E,得A‖A日E1A≠0， 故A可逆，在AA=E两边左乘以(A）即可 得出()=A由A‖A车1，有目A 或者，由可逆矩阵的定义中A,B的对等位置知 A,B互为逆矩阵，因此(A）=B=A 可逆 定义 河套大学《线性代数》课件 第二章矩阵 快东学司

可逆，则 快乐学习 以人 2.3.3 可逆矩阵的性质 为本 河套大学《线性代数》课件 第二章 矩阵 A −1 A ( ) , 1 1 A = A − − | | | | . −1 −1 A = A 性质2.3.1 若 也可逆，且 A A = E −1 | || | | | 1, 1 = = − A A E | | 0, 1  − A −1 A A A = E −1 1 1 ( ) − − A ( ) . 1 1 A = A − − | || | 1, 1 = − A A | | | | . −1 −1 A = A 证明 由 ，得 故 可逆，在 两边左乘以 得出 由 有 即可 A, B ( ) . 1 1 1 A = B = A − − − 或者，由可逆矩阵的定义中 的对等位置知 A, B 互为逆矩阵，因此 可逆 定义

水人 2.3.3可逆矩阵的性质（续1） 尚本 性质2.32若矩阵A可逆，则矩阵 A也可逆，且 (A)=(A)P 证明由 AA=E,得 (AT=(44=ET=E 性质2.3.2表明，求矩阵的逆和求矩阵的转置这两 种运算可以交换次序 河套大学《线性代数》课件 第二章矩阵 快东骨司

可逆，则矩阵 也可逆, 且 快乐学习 以人 为本 河套大学《线性代数》课件 第二章 矩阵 2.3.3 可逆矩阵的性质（续1） A T A ( ) ( ) . T −1 −1 T A = A 性质2.3.2 若矩阵 A A = E −1 ( ) ( ) . 1 T T 1 T T A A = AA = E = E − − 证明 由 ，得 性质2.3.2表明，求矩阵的逆和求矩阵的转置这两 种运算可以交换次序

水人 2.3.3可逆矩阵的性质（续2） 尚本 性质2.3.3若矩阵A可逆，数1≠0，则14 也可逆，且 (4)1= 证明 得0 从而命题的结论成立。 河套大学《线性代数》课件 第二章矩阵 快东骨司

快乐学习 以人 为本 河套大学《线性代数》课件 第二章 矩阵 2.3.3 可逆矩阵的性质（续2） A 可逆，数   0 A . 1 ( ) −1 −1 A = A   ( ) , 1 ( ) 1 1 1 A A  A A = E       =       − −     性质 2.3.3 若矩阵 ，则 也可逆，且 证明 从而命题的结论成立

水人 2.3.3可逆矩阵的性质（续3） 尚本 性质2.3.4若方阵A,B可逆，则AB也可逆， 且 (AB)=B4 证明 (ABX(BA)=A(BB-)A=AEA=A4=E. 一切从定 义出发 河套大学《线性代数》课件 第二章矩阵 快东骨司

快乐学习 以人 为本 河套大学《线性代数》课件 第二章 矩阵 2.3.3 可逆矩阵的性质（续3） A, B 可逆，则 AB 也可逆， ( ) . −1 −1 −1 AB = B A 性质 2.3.4 若方阵 且 证明 ( )( ) ( ) . 1 1 1 1 1 1 AB B A = A BB A = AEA = AA = E − − − − − − 一切从定 义出发 体会

水人 2.3.3可逆矩阵的性质（续4） 尚本 在生活中也有这样的例子例如，用A表示穿 袜子，B表示穿鞋，则A口表示脱袜子，B表示脱鞋 在穿的时候应当先穿袜后穿鞋，顺序是B、脱的顺 序就应当反过来：先脱鞋后脱袜，就是B,这 也是 (AB)=BAH的一个例子，公式 (AB)=B-A- 也称为穿脱原理 河套大学《线性代数》课件 第二章矩阵 快乐骨司

表示脱袜子， 快乐学习 以人 为本 河套大学《线性代数》课件 第二章 矩阵 2.3.3 可逆矩阵的性质（续4） A B 在生活中也有这样的例子.例如，用 表示穿 袜子， 表示穿鞋， −1 A −1 则 B 表示脱鞋. AB , −1 −1 B A 1 1 1 ( ) − − − AB = B A 1 1 1 ( ) − − − AB = B A 在穿的时候应当先穿袜后穿鞋，顺序是 序就应当反过来：先脱鞋后脱袜，就是 也是 的一个例子. 公式 也称为穿脱原理. . 脱的顺 这