山东建筑大学：《高等数学》课程教学资源（PPT课件讲稿）第一章 函数与极限 第一节 函数

第一章 函数与极限 高等数学少学时 第一章品数与极限 第一节 函数 第二节 数列的极限 第三节 函数的极限 第四节 无穷小量与无穷大量 第五节 函数极限的运算 第六节 无穷小量的比较 第七节 函数的连续性 第一章 习题课 北京邮电大学出版社

1 第一章 函数与极限 第一节 函数 第二节 数列的极限 第三节 函数的极限 第四节 无穷小量与无穷大量 第五节 函数极限的运算 第六节 无穷小量的比较 第七节 函数的连续性 第一章 习题课

第一章 函数与极限 高等数学少学时 第一节福数 函数概念 二 函数的几种特性 三、 反函数与复合函数 四、初等函数 五、函数的参数方程 北京邮电大学出版社

2 第一节 函数 一、 函数概念 二、 函数的几种特性 三、 反函数与复合函数 四、 初等函数 五、 函数的参数方程

第一章 函数与极限 高等数学少学时 一、 函数概念 定义设D是一个非空数集，对于D内任意数x,按确定的 法则f,都有唯一确定的数值y与它对应，则称这种对应关系为集 合D上的一个函数，记作 自变量 因变量 y=f(x)x∈D. 其中x称为自变量，y称为因变量，D 称为函数f的定义域，所有函数值fx) 构成的集合yy=f(x,x∈D}称为 函数f的值域. 定义域 值域 北京邮电大学出版社

3 定义 称为函数 f 的定义域,所有函数值f (x) 其中x 称为自变量，y 称为因变量，D 一、函数概念 设D是一个非空数集，对于D内任意数x ，按确定的 法则 f ,都有唯一确定的数值y与它对应， 合D上的一个函数，记作 则称这种对应关系为集 构成的集合 y = f (x), x D. 函数 f 的值域. y y = f (x), x  D x y D W f 自变量 因变量 定义域 值域 称为

第一章 函数与极限 高等数学少学时 注①f表示自变量x与因变量y之间的对应法则，而f(x)表 示x对应的函数值 ②定义域和对应法则是确定函数的两要素 ③表示函数的主要方法有三种：表格法、图形法、解析法 北京邮电大学出版社 4

4 注 ① f 表示自变量x与因变量y之间的对应法则，而f ( x )表 示x 对应的函数值. ② 定义域和对应法则是确定函数的两要素. ③ 表示函数的主要方法有三种：表格法、图形法、解析法

第一章 函数与极限 高等数学少学时 下面举几个函数的例子 例1平面上以原点(0,0)为圆心，半径为1的圆周上点的坐标 满足方程x2+y2=1.这个方程确定了变量x和y之间的关系.对于 每一个x∈1，，总有确定的y与之对应，但这个y有时不是唯一 的，这样的对应法则并不符合函数的定义，习惯上我们称这种 法测确定了一个多值函数.对这个多值函数如果附加条件≥0 (或0)按照这个法则就确定了函数y=V1-x2(或y=-V1-x2) 我们称这样得到的函数为多值函数的单值分支. 北京邮电大学出版社

5 2 y = 1− x 平面上以原点(0,0)为圆心，半径为1的圆周上点的坐标 1. 2 2 满足方程 x + y = 这个方程确定了变量x 和y之间的关系.对于 每一个 x−1,1, 总有确定的y与之对应，但这个y有时不是唯一 的，这样的对应法则并不符合函数的定义，习惯上我们称这种 法则确定了一个多值函数. 对这个多值函数如果附加条件y≥0 (或y≤0)按照这个法则就确定了函数 2 (或 y = − 1− x ). 我们称这样得到的函数为多值函数的单值分支. 下面举几个函数的例子. 例1

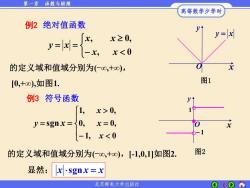
第一章 函数与极限 高等数学少学时 例2绝对值函数 y↑ x≥0， y=x 的定义域和值域分别为(-o,+o), 式 [0,+o),如图1. 图1 例3符号函数 1, x>0, y=sgnx=0, x=0, X -L,x<0 的定义域和值域分别为(-oo,+o),【-1,0,1]如图2. 图2 显然： x.sgnx=x 北京邮电大学出版社 6

6 例3 符号函数      −  =  = 1, 0 0, 0, 1, 0, x x x y 显然： x sgn x = x sgn x = 的定义域和值域分别为(-∞,+∞)，[-1,0,1]如图2. 例2 绝对值函数    −   = = , 0 , 0, x x x x y x 的定义域和值域分别为(-∞,+∞)， [0,+∞),如图1. y = x O x y 图1 1 O x • y   − 1 图2

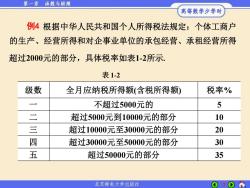
第一章 函数与极限 高等数学少学时 例4根据中华人民共和国个人所得税法规定：个体工商户 的生产、经营所得和对企事业单位的承包经营、承租经营所得 超过2000元的部分，具体税率如表1-2所示. 表1-2 级数 全月应纳税所得额（含税所得额） 税率% 不超过5000元的 5 二 超过5000元到10000元的部分 10 三 超过10000元至30000元的部分 20 四 超过30000元至50000元的部分 30 五 超过50000元的部分 35 北京邮电大学出版社

7 例4 级数 全月应纳税所得额(含税所得额) 税率% 一 不超过5000元的 5 二 超过5000元到10000元的部分 10 三 超过10000元至30000元的部分 20 四 超过30000元至50000元的部分 30 五 超过50000元的部分 35 的生产、经营所得和对企事业单位的承包经营、承租经营所得 超过2000元的部分，具体税率如表1-2所示. 表 1-2 根据中华人民共和国个人所得税法规定：个体工商户

第一章 函数与极限 高等数学少学时 试写出某个体户月收入x元与应交纳税款之间的函数关 系，并指明定义域。 解按税法规定当x≤2000元时，这时税款额y=0. 当2000<x≤7000元时，纳税部分是x-2000,应纳5%的税， 税款额为y= 5(x-2000) 1 (x-2000), 100 20 当7000<x≤12000元时，其中2000元不纳税，5000元应纳 5%的税，剩余的部分x-7000按10%纳税，此时税款额为 y=250+ 10(x-7000) 100 =250+1(x-7000, 10 北京邮电大学出版社

8 试写出某个体户月收入x元与应交纳税款y之间的函数关 系，并指明定义域. 解 ( 2000). 20 1 100 5( 2000) = − − = x x y 按税法规定当 x ≤ 2000元时，这时税款额 y = 0. 当2000 < x ≤ 7000元时，纳税部分是x–2000,应纳5%的税， 税款额为 当7000 < x ≤ 12000元时，其中2000元不纳税，5000元应纳 5%的税，剩余的部分x -7000按10%纳税，此时税款额为 ( 7000). 10 1 250 100 10( 7000) 250 = + − − = + x x y

第一章 函数与极限 高等数学少学时 类似地，当12000<x≤32000时，税款额为 y=750+5c-1200, 当32000<x≤52000时，税款额为 y=4750+0(x-32000) 当52000<x时，税款额为 y=10750+30x-520 于是所求函数关系为 北京邮电大学出版社

9 类似地，当12000 < x ≤ 32000时，税款额为 ( 12000). 5 1 y = 750+ x − 当32000 < x ≤ 52000时，税款额为 ( 32000). 10 3 y = 4750+ x − 当52000 < x 时，税款额为 ( 52000). 20 7 y = 10750 + x − 于是所求函数关系为

第一章 函数与极限 高等数学少学时 0, x≤2000， 1 (x-2000), 2000≤x≤7000， 20 250 10x-7000,7000<x≤1200， y= 750+5(-1200,12000<x≤3200， 3 4750+ (x-32000),32000<x≤52000， 10 10750+720(x-52000,5200<x. 其定义域为[0，+∞). 北京邮电大学出版社 10

10                  + −  + −   + −   + −   −    = ( 52000), 52000 . 20 7 10750 ( 32000), 32000 52000, 10 3 4750 ( 12000), 12000 32000, 5 1 750 ( 7000), 7000 12000, 10 1 250 ( 2000), 2000 7000, 20 1 0, 2000, x x x x x x x x x x x y 其定义域为[0,+∞)