上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.3-Relative Constraint

3.3 Constraint between pairs of bodies Relative angle constraint ·Revolute joint 。Translational joint Relative distance constraint

2022年3月11日 3.3 Constraint between pairs of bodies • Relative angle constraint • Revolute joint • Translational joint • Relative distance constraint

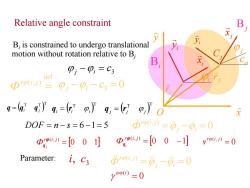
Relative angle constraint B B;is constrained to undergo translational motion without rotation relative to b B 01-p,=C3 def ro(i,j) =p,-p,-C3=0 g=ggy4,=(9,4,=69,0 x DOF=n-s=6-1=5 市9u,》=p,-p,=0 D,w=[00刂 Φ，》=[00-1 v'o,》=0 Parameter: i,C3 ro1》=0,-0,=0 ra(=0

Relative angle constraint Bi is constrained to undergo translational motion without rotation relative to Bj  j i  c3  0 def ( , )  r i j  3 c  j i  • Velocity constraint equation 0 ( , )     j i r i j     0 ( , )  j  i  r i j        3 Parameter: i, c j r Bj y  x  O j x  i y  Cj  j DOF  n  s  6 1  5   T T i i i q  r 0 0 1 ( , )  r i j j   q 0 a ( )   i  0 ( , )  r i j v    T T j j  j   q  r T T T q  qi qj 0 0 1 ( , )   r i j i   q i r i i x  i y  Bi  c

Revolute joint Definition B;is constrained to undergo rotational motion without translation relative to B, Revolute constraint

Revolute joint • Definition Bi is constrained to undergo rotational motion without translation relative to Bj Revolute constraint

Description of the constraint Inertial frame O-e Body-fixed frame of B C 4=p)' Pointo sosy) Body-fixed frame of B,C,- 4,-g,)r Point p 5s=(kPyP）y Point P and Q coincide 9-=0r9-r=07+s9-1-s=0 def 鸿=+9 D》=r+A,s9-r-As”=0 =+

• Description of the constraint Bj y  x  O j x  j y  Cj j r  Q Q j r Q j s e  Inertial frame O  C j j e  Body-fixed frame of Bj    T T j j  j q  r Point Q Q j s   Q T j Q j Q j s  x  y  Point P and Q coincide def ( , )  r i j Φ P i s   T T i i i q  r Point P P i s   T P i P i P i s  x  y  i x  i y  Ci P ir Q j j Q j r r s      P i i P ir r s      0      P i Q j r r P i i i Q j j j r  A s  r  A s  0 Bi i r   0 P i Q j r r     0 P i i Q j j r s r s Ci i e  Body-fixed frame of Bi  P

DuW=了+A,s9-1-AsP=0 Number of constraint s=2 4,=9,'9,=(9) q=gg)'=(9,yp, Degrees of freedom δ=n-S=4 n=6 Parameters of the constraint i,,s=y）,s9=(x9) Φ》= 。agg儿-

    T T , , , Q j Q j Q j P i P i P i i j s  x  y  s  x  y  s  2 Degrees of freedom   n  s  4 Number of constraint   T T j j  j q  r Parameters of the constraint        0 P i i i Q j j j r i j Φ r A s r As ( , )   T T i i i q  r     T T T T T T i j i i j  j q  q q  r r  0                                              P i P i i i i i i i Q j Q j j j j j j j r i j y x y x y x y x          sin cos cos sin sin cos cos sin ( , ) n  6 Bj y  x  O j x  j y  Cj j r  Q Q j r Q j s P i s i x  i y  Ci P ir Bi i r P

Φw)=T+A,s-片-A5y=0 A =RA Velocity constraint equation A=RAO 》=f+Asye--As”=0 重》=产+R4,s0-店-RAs,0, =0 -646业46-。 w=电，i-v》=09=(9p,) Jacobian matrix 更》=西》中列 ,》=-[R4s]Φ，D=R4s9] Right term of velocity constraint equation y"(ij)=0

j j j  A  RA j r i j Φ r   ( , )        0 P i i i Q j j j r i j Φ r A s r As ( , )        0 P i i i Q j j j r i j Φ r A s r A s      ( , )  0 • Velocity constraint equation • Jacobian matrix    0 r(i, j) r(i, j) r(i, j) Φ Φ q v q   i ii  A  RA j Q  RAjs j  i  r i P  RAisi     T T T i i j  j q  r  r    r(i, j) r(i, j) r(i, j) q qi q j Φ  Φ Φ      0                 i P i i i j Q j j j r i j       r I RA s r Φ I RA s ( , )   Q j j r i j j Φ I RA s q   ( , )   P i i r i j i Φ I RA s q    ( , ) • Right term of velocity constraint equation  0 r(i, j) v

Velocity constraint equation A,=RA 市W=产+RA,S0,-i-RAs9,=0 A=RA RR=-1 Acceleration constraint equation 0=月+RA,s6+RA,0-月-R4,s"9,-R4s0 市》=月+RA,90-月-RAs西-Asy0}+As02=0 o-业a日i4e+4食-0 r》=g》日-y》=0i=(,p,） Right term of acceleration constraint equation yu.》=A,sy9p}-A,sp

j j j  A  RA i P j i i i Q j j j r i j     Φ  r  RA s  r  RA s ( , )  0 • Acceleration constraint equation  0   i P i i i P j i i i Q j j j Q j j j            Φ  r  RA s  RA s  r  RA s  RA s r RR  I ( , ) 2 2 i P j i i Q i j j P j i i i Q j j j r i j       Φ  r  RA s  r  RA s  A s  A s • Velocity constraint equation i ii  A  RA    0 r(i, j) r(i, j) r(i, j) Φ Φ q  q     T T T i  i j  j q  r  r  • Right term of acceleration constraint equation ( , ) 2 2 i P j i i Q j j r i j   A s   A s           0                 ( , ) ~ ~ 2 2 i P j i i Q j j i P i i i j Q j j j r i j            A s A s r I IA s r Φ I IA s

Translational joint Definition: B,is constrained to undergo translational motion without rotation relative to Bi The translational motion is along a specified axis Translational constraint

2022年3月11日 理论力学CAI 运动学计算机辅助分 析 8 Translational joint Definition： – Bi is constrained to undergo translational motion without rotation relative to Bj – The translational motion is along a specified axis Translational constraint

Description of the constraint Inertial frame o-e Body-fixed frame of B,C y Define a vector attached on the axis is given Body-fixed frame of B; C,-e, a.)is given Point P and point Q are both located on the axis Define a unit vector parallel to the axis可， v is given Let h=2-”=可+9-月-，” h=r+A se-r-As

• Description of the constraint Bj y  x  O j x y j   Cj j r  Q Q j r Q j s e  Inertial frame O  C j j e  Body-fixed frame of Bj    T T j j  j q  r Q j s   Q T j Q j Q j s  x  y  Point P and point Q are both located on the axis P i s Let   T T i i i q  r P i s   T P i P i P i s  x y is given C i i e  Body-fixed frame of Bi  i x  i y  Ci Bi ir  P P ir h  Define a vector attached on the axis j v  j v is given Define a unit vector parallel to the axis i v  i v is given i v  j v  P i Q j h r r      P i i Q j j r s r s         P i i i Q j j j h  r  A s  r  A s is given

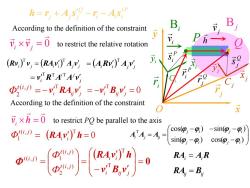
h=r+A s -r-As According to the definition of the constraint B ,×可，=0 toeitheativeoation (Rv)v,=(RAv:)A=(A Rv:)Av =VRTATAV F D》=-yRAy=-vB,y=0 According to the definition of the constraint 0to restrict P be parallel to the axis D》=(RA,）'h=0 AA=A= cos(p,-9,)-sin(p,-9,) sin(,-)cos(o;-) 。--a =0 RA=AR RA=B

According to the definition of the constraint 0    vi v j  0   vi  h      i j i i j j Rv v  RAv A v T T   0 T RAivi  h  i ij j  v RA v T   i i j j  A Rv A v T              sin( ) cos( ) cos( ) sin( ) T j i j i j i j i i j ij         A A A    0                   i ij j i i t i j t i j t i j v B v RAv h T T ( , ) 2 ( , ) ( , ) 1    to restrict the relative rotation P i i i Q j j j h  r  A s  r  A s  ( , ) 2 t i j Φ  ( , ) 1 t i j Φ Bj y  x  O j x y j   Cj j r  Q Q j r Q j s P i s i x  i y  Ci Bi ir  P P ir h  i v  j v  0 T  vi  Bijv j  RAi  AiR j i j i  v R A A v T T T RAij  Bij According to the definition of the constraint to restrict PQ be parallel to the axis