上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.5-Driving constraint

3.5 Driving constraint In addition to kinematic structure,the motion of mechanism is described by actuator inputs that specifies the time history of some position coordinates or the relative position of pairs of bodies. To uniquely determine the time history of motion of a mechanism,a number of inputs must be specified,equal in number of degrees of freedom of the system. Driving constraints are family of standard drivers
3.5 Driving constraint • In addition to kinematic structure, the motion of mechanism is described by actuator inputs that specifies the time history of some position coordinates or the relative position of pairs of bodies. • To uniquely determine the time history of motion of a mechanism, a number of inputs must be specified, equal in number of degrees of freedom of the system. • Driving constraints are family of standard drivers

3.5.1 Absolute Drivers Absolute position Driver Φad0=x-C1=x,+x”cos4,-y"sin4,-C()=0 出a=0-x-"cos4 yaxd()=C(t) C2y+G0 Xi +C (t) a0卡y-C, /cos4,C2()=0 =乙co-sirj v(=C2(t) X yo=y0+C,(0)=(sin4+Sr8s4)02+C,(0)
3.5.1 Absolute Drivers x i x i y y Pi P ir ir P i s C1(t) C2(t) cos sin ( ) 0 1 1 ( ) x C x x y i C t P i i P i i P i axd i i P i i P i axd i x y i 1 0 sin cos ( ) q ( ) 1 ( ) v C t axd i ( ) ( cos sin ) ( ) 1 2 1 ( ) ( ) C t x y C t i i P i i P i axd i ax i sin cos ( ) 0 2 2 ( ) y C y x y i C t P i i P i i P i ayd i i P i i P i ayd i x y i 0 1 cos sin ( ) q ( ) ( sin cos ) ( ) 2 2 2 ( ) ( ) C t x y C t i i P i i P i ayd i ay i ( ) 2 ( ) v C t ayd i Absolute position Driver
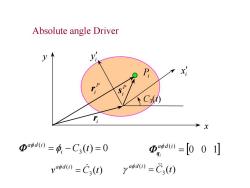
Absolute angle Driver P x C3④ X Φawdo=p,-C3(t)=0 电,do=[00刂 v0d@=C3(t) ya()=C(t)
3 ( ) 0 ( ) i C t a d i 0 0 1 ( ) a d i i q ( ) 3 ( ) C t a d i ( ) 3 ( ) v C t a d i x i x i y y Pi P ir ir P i s C3(t) Absolute angle Driver

3.5.2 Constraints between pairs of bodies (Relative constraints) A relativeΦdriver Φrd》=中,-9,-C3()=0 Φgaw=[00] Dw》=[00-] v'aa》=C3(t)) yd(iD=C(t)
3.5.2 Constraints between pairs of bodies (Relative constraints) 3 ( ) 0 ( , ) j i C t r d i j 0 0 1 ( , ) r d i j j q 0 0 1 ( , ) r d i j i q ( ) 3 ( , ) v C t r d i j ( ) 3 ( , ) C t r d i j A relative driver

A relative distance driver 西》=(-ry(-r)-C4()2=0 》=2-Y(-ryBs] Φ》=2(P-ry-(-yB, v=2C4(t)C4(t) y=y+2C4(t)C4(t)+2[C4(t)] =20-62AsP-,2As)-26-y(-) +2C4(t)C4(t)+2[C4(t)]2
A relative distance driver ( ) 0 2 4 ( , ) C t P j P i T P j P i rdd i j r r r r P i i T P j P i T P j P i rdd i j i r r r r B s q 2 ( , ) P j j T P j P i T P j P i rdd i j j r r r r B s q 2 ( , ) 2 4 4 4 2 2 2 4 4 4 2 ( ) ( ) 2[ ( )] 2 2 2 ( ) ( ) 2[ ( )] C t C t C t C t C t C t P j P i T P j P i P j j j P i i i T P j P i rdd rd r r A s A s r r r r 2 ( ) ( ) 4 4 v C t C t rdd
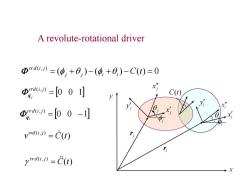
A revolute-rotational driver Φrdw》=(p+0,)-(9,+0,)-C()=0 》=[001 x y C(1) Φga-[00-1 vmau,》=C(t) 分 yrd》=C(t) X
( ) ( ) ( ) 0 ( , ) j j i i C t rr d i j 0 0 1 ( , ) rrd i j j q 0 0 1 ( , ) rr d i j qi ( ) ( , ) v C t rrd i j ( ) ( , ) C t rr d i j A revolute-rotational driver

A translational-distance driver y, C(t)is the time history of the directed distance di x between P;and P Dn=/4-C0)=0 Vi >x y,=Ad=r+A,”-r-As” Φ》=A,'(-r)+yA,s-ys”-vC()=0
( ) 0 ( , ) C t vi ij T tdd i j i v d A translational-distance driver C(t) is the time history of the directed distance between Pi and Pj ( ) ( ) 0 ( , ) viC t P i T i P ij j T j i i T i T i tdd i j v A r r v A s v s i i i v Av P i i i P ij j j j d r A s r A s

Differentiation of Φ》=4(-)+As-ys”-y,C()=0 One obtains D=A(g-)+A,T(G-)+A,s-,C0) =,yB,(y-)+A,(店-)+B,s(0-,)-vC() =yB,(g-r)+A'(G-)-,C()=0 变》=【yAB'g,-r小,Φ=A0 vaaa,》=v,C(t)
( ) ( ) 0 ( , ) viC t P i T i P ij j T j i i T i T i tdd i j v A r r v A s v s ( ) ( ) ( ) 0 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( , ) v C t v C t v C t j i i T i T j i i T i T i i j i i P ij j T j i i T i T j i i T i T i i i P ij j T j i i T i T j i i T i T i tdd i j v B r r v A r r v B r r v A r r v B s v A r r v A r r v A s Differentiation of One obtains 0 T i T i tdd i j j i T i T i T i T i tdd i j i j q v A v B r r q v A ( , ) ( , ) ( ) ( ) ( , ) v v C t i tdd i j

Differentiation of Φ》=,yB,(g-r)+yA(G-)-v,C()=0 One obtains a0=yB,(g-r)-,2yA(y,-r)+2,yB,(G-) +A(-)-y,C()=0 ya》=,2yA(y-r)-2,yB,(G-)+v,C(t)
Differentiation of One obtains ( ) ( ) ( ) 0 ( , ) j i viC t T i T j i i T i T i i tdd i j v B r r v A r r ( ) ( ) 0 ( ) ( ) 2 ( ) ( , ) 2 v C t j i i T i T i j i T i T j i i i T i T j i i i T i T i i tdd i j v A r r v B r r v A r r v B r r ( ) 2 ( ) ( ) ( , ) 2 v C t j i i T i T j i i i T i T i i tdd i j v A r r v B r r

3.5.3 Right side of velocity and acceleration equations For a kinematic constraint Φ(q=0 The associated driver is of the form Φa(q,t)=Φ(q)-C(t)=0 One obtains ①g=Φ, v4=v+C(t)=C(t) y4=x+C(t)
For a kinematic constraint The associated driver is of the form (q) 0 3.5.3 Right side of velocity and acceleration equations ( ,t) ( ) (t) 0 d q q C One obtains q q d (t) (t) d v v C C (t) d C
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.4-Gears.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.3-Relative Constraint.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.2-Absolute constraints.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.1-Basic Concepts.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_2014复杂系统动力学试卷.pdf
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)邵炜桓.pptx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)第四组-第三次作业-初稿.pptx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)第三次作业要求.pdf
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)第一次作业打分表.docx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)周一浩.pptx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)力学仿生第三次作业.pptx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)分组.docx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)仿水黾机器人(第三组).pptx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)二参数温度模型.docx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)9秦源.pptx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)9力学仿生第一次作业_吴靖瑶_鳐鱼水动力学性能在水下推进器及无人机中的应用.pptx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)8吴宇峻.ppt
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)8力学仿生第一次作业_沈晓昳_仿猫清洁擦.pptx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)7力学仿生第一次作业_陈志杰_越过山丘,无需白头.pptx
- 上海交通大学:《力学仿生——启示与探索》课程教学资源(讲课讲稿)6陈志杰.pptx
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.6-Position, velocity and acceleration analysis.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.6-Position, velocity and acceleration analysis_1.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 3_CHAP3.7-singularity.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 4_Char4-Numerical methods.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 4_Flow chart for kinematics.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 5_Planar Kinematic Modeling and Analysis.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 5_Modeling for Example 4.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 5_Modeling for Example 5.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 5_Modeling for Example2.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.1-Equations of motion of a planar rigid body.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.2 Virtual work and generalized force.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.2 Virtual work and generalized force.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.3 Equations of motion of constrained planar.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.4 Inverse Dynamics.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.5 Equilibrium Problem.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.6 Constraint reaction forces.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 7_chap7-Numerical Methods in Dynamics.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 8_Planar Dynamic Modeling and Analysis.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 8_Modeling for Example 4.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 8_Modeling for Example1.doc
