上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.2 Virtual work and generalized force

6.2 Virtual work and generalized force =+A δr°=δr+δ0，Bs 1 The virtual work of force y F δw=(6ryF =6rF+δ4yPrB,F -w4者→e

6.2 Virtual work and generalized force y x i x  i y  ir P ir P i s P Fi  P i i i P ir  r  A s P i i i i P i  r   r  B s The virtual work of force                 P i T i TP i P i i T i P i T i TP i i P i T i P i T P W i s B F F r r F s B F r F               P i T i TP i P i s B F F Q

Translational Spring-damper-actuator d,=+A”-5-AsP The virtual work of spring force y W=-f61 P=d,dy l8l=d'&M,(≠0) X 64-6-B606-879） T δl1 f=k(I-lo)+cl+F k一Spring coefficient C F=F(L,l,t) Damping coefficient F Actuator force 1-4,(6+B,6,-元-B,s®）

Translational Spring-damper-actuator P i i i P ij j j j d  r  A s  r  A s x i x  i y  ir P i s j y  j x  P j s y j r c F k ij d  o The virtual work of spring force ij T ij l  d d 2 W   f l f  k(l  l0 )  cl F l l  (l  0) ij T  dij d  i P j i i i P j j j T ij ij T ij l l  l   r B s   r B s  d d d        k Spring coefficient c Damping coefficient F Actuator force F F(l,l,t)    i P j i i i P j j j T ij l l        r B s r B s d      

The virtual work of spring force -微mm8]g-因- a-4a北1ye的-r,'aowh δl1 d f=k(1-1)+cl+F Generalized force e-r4 y 下 e- X

x i x  i y  ir P i s j y  j x  P j s y j r c F k ij d  o            j T i j T i W f l Q Q    q  q The virtual work of spring force  i ij T i TP i T j i T j TP j T ij j T ij ij T ij l l l l d r s B r s B d d d d                1        i i i  r q        j j j  r q       ij T i TP i ij i l f s B d d Q Generalized force        ij T j TP j ij j l f s B d d Q f  k(l  l0 )  cl F

Rotational Spring-damper-actuator 0,=中-中 k The virtual work of spring torque δW=-nδ0， δ0，=8，-8 n=kg(0-0)+c0n+N X 0 N=N(020,t) Torsional spring coefficient Ce Torsional damping coefficient N Actuator torque

Rotational Spring-damper-actuator ij   j i The virtual work of spring torque W  nij n  k (ij  0 )  c  ij  N ij   j i  k Torsional spring coefficient  c Torsional damping coefficient N Actuator torque N N( , ,t) ij ij   x i x  i y  j y  j x  y c F k  ij o j x  i x 

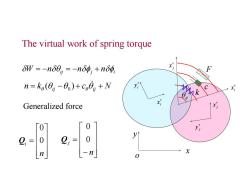
The virtual work of spring torque δW=-no0,=-no冲，+no冲， n=kg(0,-8)+c0,+N k x Generalized force x 0 2 0 n X 0

The virtual work of spring torque W  nij  n j  ni n  k (ij  0 )  c  ij  N x i x  i y  j y  j x  y c F k  ij o j x  i x         n i 0 0 Q Generalized force        n j 0 0 Q

Question What is the main difference between the force element and the kinematic joint? Force element Kinematic joint Compliant connection Rigid connection Do not change Eliminate degree degree of freedom of freedom

Question What is the main difference between the force element and the kinematic joint? Force element Kinematic joint Compliant connection Rigid connection Eliminate degree of freedom Do not change degree of freedom