上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_双摆动力学仿真说明
Dynamic Analysis of Double Pendulum 2 B2 Link BI is connected to the ground with revolute joint O,connect to B2 with revolute joint 4. Given parameters: m1=m2=m,1=l2=1,m=1kg,1=1m Initial condition 4(0)=0,4,(0)=0,,(0)=0,p2(0)=0 go-日0000,9o-p0000o Calculate time histories ofRR Constraint equation 1 xcos y Φ= ysin 中 ,0= X2 2c0s0-x- 2 cosd X2 片-2sin4-y-2sin4 2 Jacobian and right side of acceleration equation
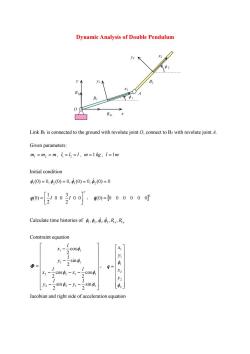
Dynamic Analysis of Double Pendulum Link B1 is connected to the ground with revolute joint O, connect to B2 with revolute joint A. Given parameters: m1 m2 m , 1 2 l l l , m 1 kg , l 1m Initial condition (0) 0, (0) 0, (0) 0, (0) 0 1 2 1 2 T l l 0 0 2 3 0 0 2 1 q(0) , T q(0) 0 0 0 0 0 0 Calculate time histories of 1 2 1 2 1 1 , , , , , R x R y Constraint equation 2 2 1 1 2 2 1 1 1 1 1 1 sin 2 sin 2 cos 2 cos 2 sin 2 cos 2 l y l y l x l x l y l x , 2 2 2 1 1 1 y x y x q Jacobian and right side of acceleration equation

10sim4000 -2c0s4 21 01-cos4,00 2sin4 ,= y= 2 -10 sin 1 0 2 2c0s4- 2 2 0-1-2c0s401-2cos4 Solve &]图- m 0 m -mg ml2/12 M= Q1= 0 心 mg ml2/12 0 Rx=-,R,=-九2 For each time step,solve AX=B 4gx[[图- 头 丐 Let y=q= 3=9= 元2 y 乌 Differential equation: Initial condition y(0)] 4(0) ,0 (0)
1 2 1 2 1 1 cos 2 cos 0 1 2 0 1 sin 2 sin 1 0 2 1 0 cos 0 0 0 2 0 1 sin 0 0 0 2 1 0 l l l l l l q , 2 2 1 2 2 1 2 2 1 2 2 1 1 2 1 1 2 1 sin 2 sin 2 cos 2 cos 2 sin 2 cos 2 l l l l l l Solve T A M q Q q q 0 /12 /12 2 2 ml m m ml m m M , 0 0 0 0 mg mg A Q 1 1 1 2 , R x R y For each time step, solve A X B 1 2 , , T A q q M X q Q A X B X 0 Let 1 1 1 1 2 2 2 x y x y y q , 1 1 1 2 2 2 2 x y x y y q Differential equation: 1 2 2 1 X y y y Initial condition (0) (0) (0) (0) 2 1 q q y y
Flow chart 开始00 9=90, 9=4o 计算A= M B= Lx] 0 是 A奇异 > 香 解方程AX=B,得到X=XIX, 令s=4,r=9 对方程 5=r, s(to)=90 积分一次 r=X1, r(to)=90 ↓ 1=1。+41,q=s(),9=r(t),违约校正 0-t 90=9 90=9 [Imax 是 否 结
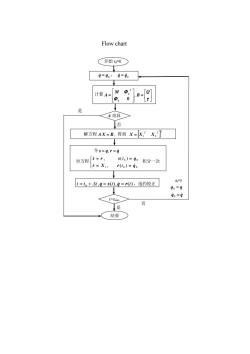
Flow chart 开始 t0=0 0 q q , 0 q q 计算 Q B M A , 0 q T q 解方程 A X B, 得到 T T T X X1 X2 是 结束 对方程 1 0 0 0 0 , ( ) , ( ) r X r q s r s q t t 积分一次 令 s q, r q , ( ), ( ) 0 t t t q s t q r t ,违约校正 是 否 q q 0 t0=t A 奇异 t>tmax 否 q q 0
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_动力学附加题.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_动力学上机_静平衡条件说明.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_动力学上机_双摆动力学逆问题说明.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_动力学上机_双摆动力学仿真说明.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 8_Modeling for Example2.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 8_Modeling for Example1.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 8_Modeling for Example 4.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 8_Planar Dynamic Modeling and Analysis.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 7_chap7-Numerical Methods in Dynamics.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.6 Constraint reaction forces.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.5 Equilibrium Problem.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.4 Inverse Dynamics.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.3 Equations of motion of constrained planar.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.2 Virtual work and generalized force.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.2 Virtual work and generalized force.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.1-Equations of motion of a planar rigid body.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 5_Modeling for Example2.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 5_Modeling for Example 5.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 5_Modeling for Example 4.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 5_Planar Kinematic Modeling and Analysis.ppt
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_双摆动力学逆问题说明.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_运动学上机_运动学计算流程图.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_运动学计算流程图.doc
- 上海交通大学:《复杂系统动力学计算机辅助分析》课程教学资源_静平衡条件说明.doc
- 上海交通大学:《人体生物力学》课程教学资源(讲义)人体生物力学概论(梁夫友).pdf
- 上海交通大学:《人体生物力学》课程教学资源(讲义)心血管生物力学及其在疾病诊疗方面的应用.pdf
- 上海交通大学:《人体生物力学》课程教学资源(讲义)运动生物力学及组织损伤机理、计算机辅助手术.pdf
- 上海交通大学:《人体生物力学》课程教学资源(讲义)生物力学的发展前景.pdf
- 《力学改变生活》课程教学资源(文献资料)The First Sounds of Merging Black Holes.pdf
- 《力学改变生活》课程教学资源(文献资料)Observation of Gravitational Waves from a Binary Black Hole Merger.pdf
- 上海交通大学:《材料热力学》教学资源_2018 lecture 4 second law II.pdf
- 上海交通大学:《材料热力学》教学资源_2018 lecture 5 property relation.pdf
- 上海交通大学:《材料热力学》教学资源_2018 lecture 6 property relation II.pdf
- 上海交通大学:《材料热力学》教学资源_2018 lecture 7 equilibrium.pdf
- 上海交通大学:《材料热力学》教学资源_2018 lecture 8 chemical equilibrium.pdf
- 西安交通大学:《材料力学 Mechanics of Materials》课程教学资源(课件讲稿)第一部分 基本变形(共六章,主讲:殷民).pdf
- 西安交通大学:《材料力学 Mechanics of Materials》课程教学资源(课件讲稿)第二部分 组合变形(共三章,主讲:殷民).pdf
- 西安交通大学:《材料力学 Mechanics of Materials》课程教学资源(课件讲稿)第三部分 专题讨论(共四章,主讲:殷民).pdf
- 东莞理工学院:《材料力学 Mechanics of Materials》课程教学大纲.pdf
- 东南大学土木工程学院:《材料力学 Mechanics of Materials》课程教学资源(考核要求).pdf
