上海交通大学：《材料热力学》教学资源_2018 lecture 6 property relation II

Contents of Today S.J.T.U. Phase Transformation and Applications Review previous Property relation Functions F and G Partial molar quantities Property relation derived from U,H,F,and G etc. SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II Contents of Today Review previous Property relation Functions F and G Partial molar quantities Property relation derived from U, H, F, and G etc

3.2 The Functions F and G(3) S.J.T.U. Phase Transformation and Applications U PV TS H≡J+PV G=H-TS F=U-TS SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II 3.2 The Functions F and G (3) F U −TS G  H −TS H U +PV

3.2 The Functions F and G(4) S.J.T.U. Phase Transformation and Applications dU=Tds-Pav dF=-SdT-Pdv Pt H dG=-SdT+VdP S dH TdS+Vdp F U SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II 3.2 The Functions F and G (4) dU =TdS−PdV dF = −SdT−PdV dG= −SdT+VdP dH =TdS+VdP

3.3 Chemical Potentials (5) S.J.T.U. Phase Transformation and Applications &G On T,P,nj≠n G OF aH aU on; on =4 T,P.nj+ni oni),+m P.S,ni+ni V.S.n;+ni The chemical potential of the component i. G H Used extensively in the treatment of the thermodynamics of solutions and of chemical reactions. SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II 3.3 Chemical Potentials (5) j i T V nj ni i T P n n ni F n G             =           , , , , i i T P nj ni i T V nj ni i P S nj ni i V S nj ni n U n H n F n G =            =           =           =           , ,  , ,  , ,  , ,  i The chemical potential of the component i. Used extensively in the treatment of the thermodynamics of solutions and of chemical reactions

Review S.J.T.U. Phase Transformation and Applications 当系统由始态经过某一过程变到终态Ⅱ后，如能使系统再回到原态，同时 也消除了原过程对环境所产生的一切影响，则原来过程称为可逆过程。 H=U+PV dU=TdS-Pdv PW G=H-TS dF=-SaT-Pav TS F=U-TS dG=-SaT+Vdp G H dH=TaS+Vdp U The chemical potential of the component i. &G OF aH aU Oni T,P,n≠n On, On O =4 i )p.S.nj+m i Jv S,nj+m SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II Review F U −TS G  H −TS H U +PV 当系统由始态I经过某一过程变到终态II后，如能使系统再回到原态，同时 也消除了原过程对环境所产生的一切影响，则原来过程称为可逆过程。 dU =TdS−PdV dF = −SdT−PdV dG= −SdT+VdP dH =TdS+VdP i i T P nj ni i T V nj ni i P S nj ni i V S nj ni n U n H n F n G =            =           =           =           , ,  , ,  , ,  , ,  i The chemical potential of the component i

Entropy of Mixing (1) S.J.T.U. Phase Transformation and Applications To calculate the entropy of mixing of two ideal gases. One gas expands isothermally from V to Vr in the apparatus shown schematically below. nR VT ideal gas Initially ds-nkdvn rdiny evacuated S2-S,=nRInV H U SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II Entropy of Mixing (1) dV n Rd V V nR dS T a T a V V V V S S ln 2 1    = = To calculate the entropy of mixing of two ideal gases. ideal gas V nR T P V S T V  =         =        Va VT Initially evacuated One gas expands isothermally from Va to VT in the apparatus shown schematically below. a T V V S2 − S1 = nRln

Entropy of Mixing (2) S.J.T.U. Phase Transformation and Applications To calculate the entropy of mixing of two ideal gases. Because ideal gases do not interact,we can calculate the total entropy change as the sum of the two entropy changes of the individual gases. (S-S)。=,RIn'g+么 Va Va Va 2-S=nS2-S,。+m,S,-S。=%,Rn'aa+m,Rn Per mole of mixture: S-S=”Rn。 +业+ nbRnVb Va+Vo na+np na+np n+np H SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II Entropy of Mixing (2) To calculate the entropy of mixing of two ideal gases. Because ideal gases do not interact, we can calculate the total entropy change as the sum of the two entropy changes of the individual gases. ( ) a a b a a V V V S S n R + 2 − 1 = ln Va VT Vb ( ) ( ) b a b b a a b a a b b a V V V n R V V V S S n S S n S S n R + + + 2 − 1 = 2 − 1 + 2 − 1 = ln ln Per mole of mixture: b a b a b b a a b a b a a b V V V R n n n V V V R n n n n n S S + + + + + = + − ln ln 2 1

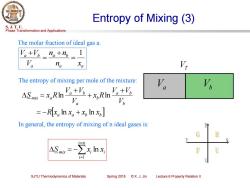
Entropy of Mixing (3) S.J.T.U. Phase Transformation and Applications The molar fraction of ideal gas a. V。+'a-n。+n=1 na Xa The entropy of mixing per mole of the mixture: Va Va AS.-s,ki V =-R[x Inx。+x,lnx] In general,the entropy of mixing of n ideal gases is: i=1 SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II Entropy of Mixing (3) The molar fraction of ideal gas a. Va VT a a a b a a b n x n n V V V 1 = + = + Vb   a a b b b a b b a a b mix a R x x x x V V V x R V V V S x R ln ln ln ln = − + + + +  = In general, the entropy of mixing of n ideal gases is: The entropy of mixing per mole of the mixture:  = =  = − i n i mix i i S x x 1 ln

On Gibbs free energy S.J.T.U. Phase Transformation and Applications -lw=-oW +oW actual Slw T T &Q=dUU-δW dS≥ T 2=dU+p外dV-oW' TdS-du-pndV-W 有效功 SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II On Gibbs free energy −lw= −Wrev +W T lw T Q dS  actual  = − T Q dS  actual  Q = dU + p 外dV −W' TdS −dU − p 外dV  −W' Q = dU −W 有效功

On Gibbs free energy S.J.T.U. Phase Transformation and Applications TdS-dU-p外dV≥-W' dT=0,dp外=dp=0 TdS-dU-pdW≥-oWW -dU+pV-TS)r,p≥-ow -d(Gh,p≥-w 等号表示可逆过程，即：在定温定压条件下，系统Gibbs自 由能的减少等于系统所作的最大有效功。 SJTU Thermodynamics of Materials Spring2018©X.J.Jin Lecture 6 Property Relation Il

Phase Transformation and Applications S. J. T. U. SJTU Thermodynamics of Materials Spring 2018 © X. J. Jin Lecture 6 Property Relation II On Gibbs free energy TdS −dU − p 外dV  −W' dT = 0, dp外 = dp = 0 TdS−dU − pdV  −W' ( ) ' − d U + pV −TS T , p  −W ( ) ' − d G T , p  −W 等号表示可逆过程，即：在定温定压条件下，系统Gibbs自 由能的减少等于系统所作的最大有效功