上海交通大学：《复杂系统动力学计算机辅助分析》课程教学资源_Chapter 6_Char6.4 Inverse Dynamics

6.4 Inverse Dynamics of Kinematically Driven systems For dynamic system with only kinematic constraints Mi+D,九=2 nh×3nb 中，i=Y nh≤3nb If driving constraints are appended to the kinematic constraints ΦK Φ= =0,Φ：(3nb-nh)×1 3nb×3nb 1f西，g,≠0, such problem is an inverse dynamic problem

6.4 Inverse Dynamics of Kinematically Driven systems        q Mq Q q q   T A If driving constraints are appended to the kinematic constraints For dynamic system with only kinematic constraints nh nb nh nb 3 3   q   : (3  ) 1        nb nh D D K     0, 3nb  3nb  q (q,t)  0,  q If such problem is an inverse dynamic problem

If，(,)≠0， Equations M+Φ，九=04 may be solved Φ，i=Y i=Φ，y=西，'№4-M λ= Lagrange multiplier associated with the driving constraints,which is used for determining the forces and torques that would be required to impose the driving constraints

       q Mq Q q q   T A   1  q q   Q Mq q     T A 1   (q,t)  0,  q If Equations may be solved        D K    : D  Lagrange multiplier associated with the driving constraints, which is used for determining the forces and torques that would be required to impose the driving constraints

Example 6.7 X Single pendulum is shown in the figure.The length of the pendulum is 21,and the mass of the pendulum is m.The pendulum is applied with gravitational force.The kinematic driver is given by ΦD=-3π/2-2t=0 1.Write the acceleration constraint equation X 2.Write the Lagrange equation of the first kind 3.Write the mixed algebraic-differential equation 4.Find the Lagrange multipliers 5.Give a physical interpretation of each Lagrange multiplier

Example 6.7   3 / 2  2 t  0 D     x1 y1 C x y  g Single pendulum is shown in the figure. The length of the pendulum is 2l, and the mass of the pendulum is m. The pendulum is applied with gravitational force. The kinematic driver is given by 2. Write the Lagrange equation of the first kind 1. Write the acceleration constraint equation 3. Write the mixed algebraic-differential equation 5. Give a physical interpretation of each Lagrange multiplier 4. Find the Lagrange multipliers

Solution: X Kinematic driver ΦD=p-3π/2-2t=0 Constraint equations 中 x-1cos Φ= y-lsinφ =0 g φ-3π/2-2t Xi Acceleration constraint equation Φ，i=y Length 27 101sinφ -Icosoo2 Mass m y=-Isin2 0

Solution:  0            t y l x l      3 / 2 2 sin cos          0 0 1 0 1 cos 1 0 sin   l l  q         0 sin cos 2 2     l l    3 / 2  2 t  0 D Kinematic driver     Constraint equations Acceleration constraint equation  q   q  x1 y1 C x y  g Length 2l Mass m

Acceleration constraint equation 10lsinφ Icos2 01-1cosφ =一 Isingo2 001 Dynamic equations of the first kind m 0 0 m 0 22 三 -mg n-2 0 0 -1cosoo2 21 ml cos 9o2 > i= 护 -Isin2 九2 -mg mlsin o2 0 元3-mgl cos

               0 sin cos 2 2          l l y x q                       cos sin cos 2 2 3 2 1 mgl mg ml ml   Dynamic equations of the first kind                                   0 0 sin cos 1 0 1 0 1 0 0 0 0 / 3 0 0 0 0 3 2 1 2 mg l l y x ml m m                               0 sin cos 0 0 1 0 1 cos 1 0 sin 2 2           l l y x l l Acceleration constraint equation

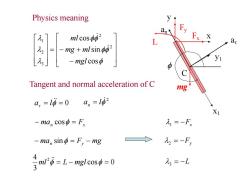
Physics meaning 「2]「mio02 元2 -mg +mlsin2 -mglcos Tangent and normal acceleration of C mg a,=1币=0an=l02 Xi -ma cos=F 九1=-F -ma sino=F-mg 九2=-F, 等m3=1-g1cs=0 九3=-L

Physics meaning x1 y1 C x y  mg at an Fx Fy L                       cos sin cos 2 2 3 2 1 mgl mg ml ml      0 t  a l 2   a l n  Tangent and normal acceleration of C m n Fx  a cos  ma F mg  n sin  y  cos 0 3 4 2 ml   L  mgl    2  Fy 3  L 1  Fx

Example 6.8 Double pendulum is shown in the figure. The length of each pendulum is 21,and the mass of each pendulum is m.Each X pendulum is applied with gravitational force.The kinematic driver is given by Length 27 Mass m ,-4- y2 8 1.Write the acceleration constraint equation X 2.Write the Lagrange equation of the first kind 2 3.Write the mixed algebraic-differential equation 4.Find the Lagrange multipliers 5.Give a physical interpretation of each Lagrange Length 21 x2 multiplier Mass m

Example 6.8 x1 y1 C1 x y 1 g x2 y2 C2 2 Length 2l Mass m Length 2l Mass m Double pendulum is shown in the figure. The length of each pendulum is 2l, and the mass of each pendulum is m. Each pendulum is applied with gravitational force. The kinematic driver is given by 2. Write the Lagrange equation of the first kind 1. Write the acceleration constraint equation 3. Write the mixed algebraic-differential equation 5. Give a physical interpretation of each Lagrange multiplier 4. Find the Lagrange multipliers 0 15 2 3 15 5 2 1 1                 t t D       

Solution Kinematic driver X DD = =0 o Length 27 Mass m Kinematic constraint equations ,y2 g 月 Length 21 X2 Mass m

                   0 0 sin cos 0 cos sin 1 1 1 1 1 1 l y x     Kinematic driver Kinematic constraint equations x1 y1 C1 x y 1 g x2 y2 C2 2 Length 2l Mass m Length 2l Mass m                              sin cos 0 cos sin sin cos 0 cos sin 2 2 2 2 2 2 1 1 1 1 1 1 l y l x y x         0 15 2 3 15 5 2 1 1                 t t D        Solution:

Constraint equations x-Icos y-Isin Φ= x2-1cos-x-1cos =0 y2-Isin-y-Isin 4-5π/3-t/15 42-4-2t/15 Acceleration equation Φ，i=Y 「101sin00 0 -1cos,,2 01-1cos4100 -Isin2 -1 0 Isin 1 0 Isin2 -1cos,2-1c0sp222 Da= Y= 0-1-1cos4,01-1cosφ2 -Isin2-Isin 0 0 00 0 -1 00 0

 0                  2 /15 5 / 3 /15 sin sin cos cos sin cos 2 1 1 2 2 1 1 2 2 1 1 1 1 1 1 t t y l y l x l x l y l x l              Constraint equations Acceleration equation  q   q               0 0 1 0 0 1 0 0 1 0 0 0 0 1 cos 0 1 cos 1 0 sin 1 0 sin 0 1 cos 0 0 0 1 0 sin 0 0 0 1 2 1 2 1 1       l l l l l l  q              0 0 sin sin cos cos sin cos 2 2 2 2 1 1 2 2 2 2 1 1 2 1 1 2 1 1                   l l l l l l 

Solve equations 0 Isin 00 0 -1cos442 0 1 -1cos 0 0 0 :2 -Isin -1 0 Isin 10 Isin 西 -Icos2-1cos 0 -1-1cos4 0 1 -1cosφ2 2 -Isin42-lsin少，4， 0 0 1 0 0 0 0 0 0 -1 00 1 西 0 1 -lcos,可，2 -Isin2 西 0 元2 -2cos,,2-1cos222 2 -21sin-Isin2 可， 0

                  0 2 sin sin 2cos cos 0 sin cos 2 2 2 2 1 1 2 2 2 2 1 1 2 1 1 2 1 1 2 2 2 1 1 1                           l l l l l y x y x                          0 0 sin sin cos cos sin cos 0 0 1 0 0 1 0 0 1 0 0 0 0 1 cos 0 1 cos 1 0 sin 1 0 sin 0 1 cos 0 0 0 1 0 sin 0 0 0 2 2 2 2 1 1 2 2 2 2 1 1 2 1 1 2 1 1 2 2 2 1 1 1 1 2 1 2 1 1                                 l l l l l l y x y x l l l l l l Solve equations