《Artificial Intelligence：A Modern Approach》教学资源（PPT课件，英文版）Chapter 6-Adversarial Search

Adversarial Search Chapter 6 Section 1-4

Adversarial Search Chapter 6 Section 1 – 4

Outline ·Optimal decisions ·a-βpruning Imperfect,real-time decisions

Outline • Optimal decisions • α-β pruning • Imperfect, real-time decisions

Games vs.search problems ·"Unpredictable"opponent→specifying a move for every possible opponent reply ● ·Time limits→unlikely to find goal,.must approximate

Games vs. search problems • "Unpredictable" opponent → specifying a move for every possible opponent reply • • Time limits → unlikely to find goal, must approximate •

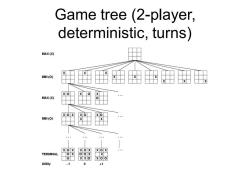
Game tree (2-player, deterministic,turns) MAX (X) MIN (O) MAX (X) X o X X o MIN (O) X o X X o X TERMINAL o x oo X x可 X oo Utility 0

Game tree (2-player, deterministic, turns)

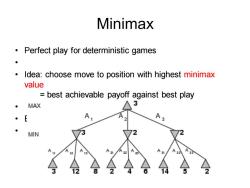
Minimax Perfect play for deterministic games ● Idea:choose move to position with highest minimax value best achievable payoff against best play MAX 3 ·E A MIN 12 21 3

Minimax • Perfect play for deterministic games • • Idea: choose move to position with highest minimax value = best achievable payoff against best play • • E.g., 2-ply game: •

Minimax algorithm function MINIMAX-DECISION(state)returns an action v←MAX-VALUE(state) return the action in SUCCESSORS(state)with value v function MAX-VALUE(state)returns a utility value if TERMINAL-TEST(state)then return UTILITY(state) U←-00 for a,s in SUCCESSORS(state)do MAX(v,MIN-VALUE(s)) return v function MIN-VALUE(state)returns a utility value if TERMINAL-TEST(state)then return UTILITY(state) U←0∞ for a,s in SUCCESSORS(state)do MIN(v,MAX-VALUE(s)) return v

Minimax algorithm

Properties of minimax Complete?Yes (if tree is finite) Optimal?Yes (against an optimal opponent) ● Time complexity?O(bm) Space complexity?O(bm)(depth-first exploration) ● 。For chess,b≈35，m≈100for"reasonable"games exact solution completely infeasible

Properties of minimax • Complete? Yes (if tree is finite) • • Optimal? Yes (against an optimal opponent) • • Time complexity? O(bm) • • Space complexity? O(bm) (depth-first exploration) • • For chess, b ≈ 35, m ≈100 for "reasonable" games → exact solution completely infeasible •

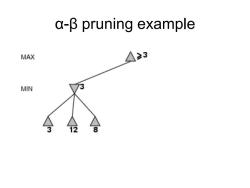
a-B pruning example MAX Λ3 MIN 73 8

α-β pruning example

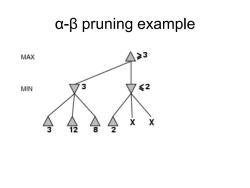
a-βpruning example MAX ≥3 MIN 3 ≤2 X X

α-β pruning example

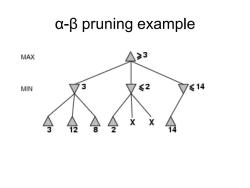
a-B pruning example MAX ≥3 MIN 3 ≤2 7≤14 X X 8 2 14

α-β pruning example