《化工热力学》课程授课教案（讲义）Chapter 3 Volumetric Properties of Pure Fluids

Chapter 3 Volumetric Properties of Pure Fluids Contents: Introduction 3.1 PVTbehavior of pure substances 3 2 Virial Fquations of state 3.3 the ideal gas 3.4 Application of the Virial Equations 3.5 Cubic equation of state 3.6 Generalized Correlations for Gases Introduction Why to study this chapter? In industrial processes,we need:Thermodynamic properties,Such as intemal energy, enthalpy.entropy.gibbs energy. etc Very important for industrv How can we obtain these Pressure Very easy to be measured Two routes: PVT temperature measuring directly We hope calculating with other which can be They can be used to calculate measured directly volumetric properties 3.1 PIT behavior of pure substances By measuring the vapor pressure,volume and temperature of a pure substances when different phases ,we can d raw the curve of p. V=constant ◆ PT diagram T=constant ◆ Py diagram P=constant Ty diagram 3.1.1PT diagram of Fluid pure substance P Vaporization curve C. For example:PT diagram of water when V=constant Fusion Critical point curve Liquid Two points: 1)C-the critical point Solid 2 Pc-the critical pressure To-the critical temperature Sublimation curve

Chapter 3 Volumetric Properties of Pure Fluids Contents： Introduction 3.1 PVT behavior of pure substances 3.2 Virial Equations of state 3.3 the ideal gas 3.4 Application of the Virial Equations 3.5 Cubic equation of state 3.6 Generalized Correlations for Gases Introduction Why to study this chapter ? In industrial processes, we need: Thermodynamic properties, Such as internal energy, enthalpy, entropy, gibbs energy, etc. How can we obtain these informations? Two routes : measuring directly calculating with other parameters which can be measured directly 3.1 PVT behavior of pure substances By measuring the vapor pressure, volume and temperature of a pure substances when different phases achieve equilibrium, we can draw the curve of P-V-T 3.1.1 PT diagram of pure substance For example: PT diagram of water when V=constant Two points: 1) C—the critical point PC—the critical pressure TC—the critical temperature V=constant PT diagram T=constant PV diagram P=constant TV diagram P V T Very important for industry Pressure Volume temperature They can be used to calculate volumetric properties Very easy to be measured We hope P T Liquid Solid Critical point Sublimation curve Fusion curve Vaporization curve Fluid C 1 2

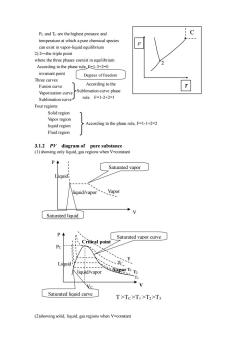
Pc and Tc are the highest pressure and temperature at which apure chemical species can exist in vapor-liquid equilibrium 2)2-the triple point where the three phases coexist in equilibrium According to the phase rule.E=1-3+2=0 invariant point Degrees of freedom Three curves: According to the Fusion curve Vaporization curve Sublimation curve phase Sublimation curve ruleF=1-2+2=l Four regions: Vapor region liquid region According to the phase rule,F=1-1+2=2 Fluid region 3.12P diagram of pure substance (1)showing only liquid,gas regions when V=constant Saturated vapor Niquid/vapor、Vapor Saturated liquid Saturated vapor curve al po vapo Saturated liquid curve T>Tc>TI>T2>T3 (2)showing solid,liquid,gas regions when V-constant

PC and TC are the highest pressure and temperature at which a pure chemical species can exist in vapor-liquid equilibrium 2) 2—the triple point where the three phases coexist in equilibrium According to the phase rule, F=1-3+2=0 invariant point Three curves: Fusion curve Vaporization curve Sublimation curve Four regions: Solid region Vapor region liquid region Fluid region 3.1.2 PV diagram of pure substance (1) showing only liquid, gas regions when V=constant (2)showing solid, liquid, gas regions when V=constant Degrees of freedom According to the phase rule, F=1-1+2=2 C p T 2 According to the Sublimation curve phase rule F=1-2+2=1 Vapor Liquid V P Saturated liquid liquid/vapor Saturated vapor Vapor T1 VC T TC PC liquid/vapor Liquid P Critical point Saturated vapor curve Saturated liquid curve V T >TC >T1 >T2 >T3 T2 T3

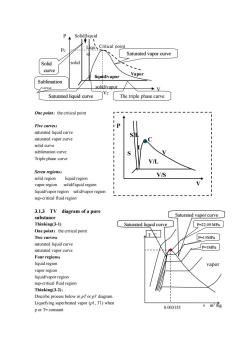
Solid/liquid gu、 Saturated vapor curve Solid solic curve liquid/apor Vapor Sublimation solid/vapor Saturated liquid curve The triple phase curve Five curves: saturated liquid curve saturated vapor curve solidcurve Triple phase curve V/L Seven regions: solid region liquid region VIS apor region solidniquidregiorn liquid/vapor region solid/vapor region sup-critical fluid region 3.1.3 TV diagram of a pure substance Saturated vapor curve Thinking(3-l) Saturated liquid curve P-22.09MP One point:the critical point Two curves: P-15MPa saturated liguid curve saturated vapor curve P-IMPa Four regions: liquid region vapo】 vapor region liquid/vapor region sup-critical fluid region Thinking(3-2): Diseribe process below diagram Liquefying superheated vapor(pl.T1)when porT=constant 0.003155

One point：the critical point Five curves： saturated liquid curve saturated vapor curve solid curve sublimation curve Triple phase curve Seven regions： solid region liquid region vapor region solid/liquid region liquid/vapor region solid/vapor region sup-critical fluid region 3.1.3 TV diagram of a pure substance Thinking(3-1) One point：the critical point Two curves： saturated liquid curve saturated vapor curve Four regions： liquid region vapor region liquid/vapor region sup-critical fluid region Thinking(3-2)： Discribe process below in pT or pV diagram. Liquefying superheated vapor (p1, T1) when p or T= constant PC VC liquid/vapor Vapor Solid/liquid solid/vapor Saturated vapor curve P V Liqu id Critical point solid Saturated liquid curve Solid curve Sublimation curve The triple phase curve P V S S/L L C V V/S V/L vapor Saturated vapor curve Saturated liquid curve T ℃ 0.003155 v m 3 /kg P=22.09 MPa P=15MPa P=1MPa

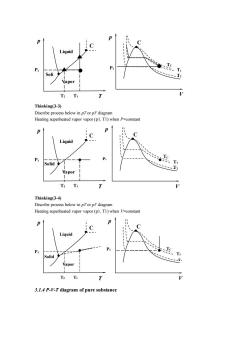
：T T 、-T Thinking(3-3) Discribe process below in Heating superheated vapor vapor (pl,Tl)when P=constan Liquid T Vapor T2 T T Thinking(3-4) Discribe process below in pTor pl diagram Heating superheated vapor vapor (pl,T1)when V-constant Liquid T 3.1.4 P-V-T diagram of pure substance

Thinking(3-3) Discribe process below in pT or pV diagram Heating superheated vapor vapor (p1, T1) when P=constant Thinking(3-4) Discribe process below in pT or pV diagram Heating superheated vapor vapor (p1, T1) when V=constant 3.1.4 P-V-T diagram of pure substance T2 T1 P1 p T Liquid Vapor Soli d C P1 p V TC C T2 T1 T2 P1 p T Liquid Vapor Solid C T1 P1 p V TC C T2 T1 P1 T2 p T Liquid Vapor Solid C T1 P1 p V TC C T2 T1

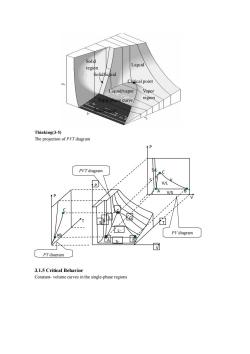
egion Ctitical point Liquid/vapor Vapo curve Thinking(3-5) The projection of PVTdiagram P V/S PV diagram A< 3.1.5 Critical Behavior Constant-volume curves in the single-phase regions

Thinking(3-5) The projection of PVT diagram 3.1.5 Critical Behavior Constant- volume curves in the single-phase regions P PV diagram PT diagram B C A L AB P T V C S V V L P T A B C S G L- G S- G S- L S/L V/L V/S PVT diagram Solid region Solid/liquid Liquid regi on Liquid/vapor Vapor region Critical point Triple phase curve Solid/vapor

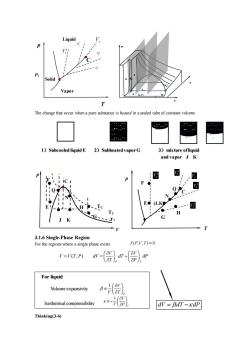
Liauid Vapor The change that occur whena pure substanceis heed nasealed tube of constant volume - 1)Subcooled liquidE 2)Subheated vaporG 3)mixture ofliquid and vapor J K pt 图 ● Q N (,K ●- H G-T T 3.1.6 Single-Phase Region For the regions where a single phase exists f(P,',T)=0 V=V(T.P) w-r)n) Forliquid Volume expansivity =】 Isothermal compressibility dv BdT-kdP Thinking(3-6)

The change that occur when a pure substance is heated in a sealed tube of constant volume 3.1.6 Single-Phase Region For the regions where a single phase exists Thinking(3-6) p T C V T1 TC C T2 p F E E F (J,K) H G N Q Vc 2 v V 1 v V 2 l V 1 l V J K N Q G H Vc V V T P = ( , ) P T V V dV dT dP T P       = +           Isothermal compressibility 1 P V V T           1 T V V P      −      Volume expansivity dV dT dP = −   For liquid V L P T A B C S G L- S-GG S- L p T Liquid Vapor Solid C P1 1 l V 2 l V Vc 1 v V 2 v V 1）Subcooled liquid E 2）Subheated vapor G 3）mixture ofliquid and vapor J K f P V T ( , , ) 0 =

features of and for liquid? 3.2 Virial Equations of state 3.2.I Introduction to EOS For a pure substance F=1Fx=C-P+2=1-1+2=2 that is:For a pure substance.fixing two of its properties fixes all the othersand thus determines its T=o(P,V)or P=W(T,V)or V=5(P,T) f(P.V,T)=0- The equation ofstate(EOS) Value of EOS EOS的价值： 1)精确地代表相当广泛范围内的PT数据，大大减少实验测定工作量。 2)可直接计算不做实验测定的其它热力学性质 3)讲行相平衡的计算 但其通用性差，要在广泛的气体密度范围内即用于极性物质，又用于非极性物质，又要精 度，很难做到。 The necessary conditions of EOS 1)According with critical condition 2)P0().according with the law of ideal gas 3.2.2 Virial Equation of State The PIproduct for a gas or vapor may be expressed as a function of P by a power series s or The PI product for a gas vapor may be expressed as a function of Pby a power series plV=a+bP+cP2+. Let c9 T b=aB,c=aC,.p=a+Bp+Cp2+） Wherea.B',C',etc.,are a=RT constants foragiven temperature and a given chemical species 3.2.3 Two forms of the Virial Equation Compressibility factor RT

features of κandβfor liquid ? 3.2 Virial Equations of state 3.2.1 Introduction to EOS For a pure substance Fmax =? Fmax =C-P+2=1-1+2=2 that is: For a pure substance, fixing two of its properties fixes all the others, and thus determines its thermonadymic state We can write: Value of EOS EOS 的价值： 1）精确地代表相当广泛范围内的 PVT 数据，大大减少实验测定工作量。 2）可直接计算不做实验测定的其它热力学性质 3）进行相平衡的计算 但其通用性差，要在广泛的气体密度范围内即用于极性物质，又用于非极性物质，又要精 度，很难做到。 The necessary conditions of EOS 1）According with critical condition 2）P→0（V→∞）, according with the law of ideal gas 3.2.2 Virial Equation of State The PV product for a gas or vapor may be expressed as a function of P by a power series The PV product for a gas or vapor may be expressed as a function of P by a power series Let Where a , B′, C′, etc., are constants for a given temperature and a given chemical species 3.2.3 Two forms of the Virial Equation Compressibility factor T P V or P T V or V P T = = =    ( , ) ( , ) ( , ) The equation of state (EOS) f P V T ( , , ) 0 = T1 p TC C T2 V 2 pV a bP cP = + + + ' ' b aB c aC = =  , , ' ' 2 pV a B P C P = + + + (1 ) a RT  PV Z RT 

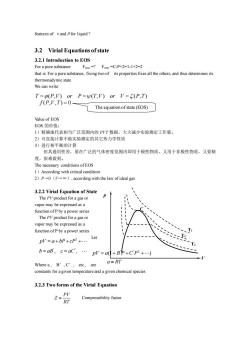
Z=1+BP+CP+Dp+- C'=C-B2 (RT) or 2=1+B B=B T B.Bissecond virial coefficients D0-38C+2B C.C is third virial coefficients,etc. (RT) For a given gas the virial coefficients are functions of temperature only The Virial equation is the only one having a firm basis in theory For the expansion in 1/V 2=1+ 、c D ++ the term B/V- -interactions between paris of molecules the term C/V2-three-body interactions,etc. Since two-body interactions are many times more common than three-body interactions. three-body inter are many four-body ir higher-ordered terms decreas rapiy 3.4 Application of the Virial Equations the Virial Equations Z=1+BP+Cp2+Dp3+. 资+品+ Z=1+B The Virial Equations are infinite series For engineering purposes,their convergence should be very rapid Thinking(3-6 May equation be truncated to two or three terms for application?When For example: Compressibility-factor graph for methane 400c 250 At low pressure,the isotherms are nearly straight lines,and approximate to tangent at P 1009 0 That is tangent can replace the isotherms at low pressure The tangent at P→0is 100) Z=1+BP =1+ Z=1+ BP 1,0002,0003,000 RT P(psia)

For a given gas the virial coefficients are functions of temperature only The Virial equation is the only one having a firm basis in theory For the expansion in 1/V the term B/V ——interactions between paris of molecules the term C/V2——three-body interactions, etc. Since two-body interactions are many times more common than three-body interactions; three-body interactions are many times more numerous than four-body interactions, etc., the contributions to Z of the successively higher-ordered terms decrease rapidly. 3.4 Application of the Virial Equations the Virial Equations For engineering purposes, their convergence should be very rapid. Thinking(3-6) May equation be truncated to two or three terms for application ? When? For example: Compressibility-factor graph for methane 2 3 1 B C D Z V V V = + + + + ┅ ' B B RT = ( ) 2 ' 2 C B C RT − = ( ) 3 ' 3 D BC B 3 2 D RT − + = or B , B′ is second virial coefficients C , C′ is third virial coefficients, etc. ' ' 2 ' 3 Z B P C P D P = + + + + 1 ┅ 2 3 1 B C D Z V V V = + + + +  The Virial Equations are infinite series. ' ' 2 ' 3 Z B P C P D P = + + + +  1 2 3 1 B C D Z V V V = + + + + ┅ At low pressure, the isotherms are nearly straight lines, and approximate to tangent at P→ 0 That is tangent can replace the isotherms at low pressure The tangent at P → 0 is 1 B Z V ' = + Z B P = +1 1 BP Z RT = +

Application range 1)The beusedtorepresent the P-V-Tbehavior of vapr,but not suitable to liquid 2)When P<1.5 Mpa,two equations as followedcan be used for engineering purpose Z=1+ B Z=1+ BP RT 3)When 1.5Mpa<P<5Mpa,the virial equation truncated to three termsoften provides excellent results 4)At high pressure,low temperature and high request of precision,the virial equation truncated to more terms can provides excellent results 应用范图与条件 维里方程无 一个理论状态方程，其计算范围应该是很宽阔的，但由于维里系数的缺乏，使 维里方程的普遍性和通用性受到了限制。在使用维里方程时应注意： A用于气相PT性质的计算，对液相不适用： B.P<L.5Ma时，用两截项维里方程计算，可满足工程要求： CL5<P<5na时，用三截项维里方程计算： D.高压，精确度要求高时，可根据情况，多取几项 目前采用维里方程计算气体PT性质时，一般最多采取三项。这是由于多于三项的维里方 程中的常数奇缺，所以多于三项的维里方程一般不大采用。 Example 3.7 Solution 3.7 (1)For an ideal gas V=RT=83.14x473.15=3934cmmo Z=1 P 10 (2)Solving virial equation truncted two terms for Vgives P Z= RT-I+RT ◆ V= RT V=R+B=3934-388=3546cmmo1r 7-00014 P (3)Solving virial equation truncted three terms for V PV BC Z=RT 1+ To facilitate iteration,writeqution above as v-0C) P V0-=3934cm3mol-1 V1=3539 cm3mol- V2=3495cm3mol-1 V=3488 cm3mol-1 [when (Vi+1-Vi)<e] Z=0.8866

Application range 1) The virial equation can be used to represent the P-V-T behavior of vapor, but not suitable to liquid 2) When P < 1.5 Mpa， two equations as followedcan be used for engineering purpose 3) When 1.5Mpa<P<5Mpa，the virial equation truncated to three terms often provides excellent results 4) At high pressure, low temperature and high request of precision，the virial equation truncated to more terms can provides excellent results 应用范围与条件 维里方程是一个理论状态方程，其计算范围应该是很宽阔的，但由于维里系数的缺乏，使 维里方程的普遍性和通用性受到了限制。在使用维里方程时应注意： A.用于气相 PVT 性质的计算，对液相不适用； B. P<1.5Mpa 时，用两截项维里方程计算,可满足工程要求； C. 1.5Mpa<P<5Mpa 时，用三截项维里方程计算； D.高压，精确度要求高时，可根据情况，多取几项。 目前采用维里方程计算气体 PVT 性质时，一般最多采取三项。这是由于多于三项的维里方 程中的常数奇缺，所以多于三项的维里方程一般不大采用。 Example 3.7 Solution 3.7 (1) For an ideal gas (2) Solving virial equation truncted two terms for V gives (3) Solving virial equation truncted three terms for V To facilitate iteration, write equation above as: V0=3934 cm3mol-1 V1=3539 cm3mol-1 V2=3495 cm3mol-1 . V=3488 cm3mol-1 [when (Vi+1 -Vi)<ε] Z=0.8866 3 1 3934 388 3546 RT V B cm mol P − = + = − = Z=0.9014 2 (1 ) RT B C V P V V = + + 1 2 (1 ) i i i RT B C V P V V + = + + 1 B Z V = + 1 BP Z RT = + 2 1 B C Z V V = + + RT V B P 1 = + PV BP Z RT RT = = + 83.14 473.15 3 1 3934 10 RT V cm mol P  − = = = Z=1 2 1 PV B C Z RT V V = = + +

3.5 Cubic equation of state Cubic equation of states are the polynomial equations that are cubic in molar volume Include mainly: (1)Van Der Waals equation (2)R-K (Redlich-Kwong equation (3)S-R-K (Soave-Ridlich-Kwang)equation （4 )P-R (Peng-Robinson equation (5）P-T(Patel-Teja）equation 3.5.1 The van der Waals Equation of State The first practical cubic equation of state was proposed by J.D.van der Waals in 1873 (p+)(V-B)=RT RT Where a,b are all constant a/W2:压力校正项b:体积校正项 When a=b=0 RT p=-b门 PΨ=RO 3.5.2 A Generic Cubic Equation of State RT e(v-n) P= P-b(W-b)r2+Ψ+2 Scores of cubic equations of state are special cases of the equation RT 0(V-n) P=-bV-b)2+W+乃) 7=bK=0 n=bK=(∈+o)b 0=a2=0y V0=a(T)1=∈σb RT a RT a(T) P-V-6V P-Y-6-V+EB)(v+ab) VDW Equation ofState Generic Cubic Equation ofState Generic Cubic Equation ofSiate

3.5 Cubic equation of state Cubic equation of states are the polynomial equations that are cubic in molar volume Include mainly: （1） Van Der Waals equation （2） R-K （Redlich - Kwong ）equation （3） S-R-K (Soave - Ridlich - Kwang) equation （4） P-R （Peng - Robinson ） equation （5） P-T （ Patel-Teja ） equation 3.5.1 The van der Waals Equation of State The first practical cubic equation of state was proposed by J. D. van der Waals in 1873 Where a, b are all constant a/V2: 压力校正项 b：体积校正项 When a=b=0 3.5.2 A Generic Cubic Equation of State Scores of cubic equations of state are special cases of the equation: Generic Cubic Equation of State 2 RT a p V b V = − − ( ) 2 a p V b RT V     + − =   2 RT a p V b V = − − PV RT = ( ) ( )( ) 2 RT V P V b V b V V     − = − − − + + VDW Equation of State Generic Cubic Equation of State  = b  = a T( )   = + ( )b 2   = b ( ) ( )( ) RT a T p V b V b V b  = − − +  +  = b  = a  = 0  = 0 2 RT a p V b V = − − ( ) ( )( ) 2 RT V P V b V b V V     − = − − − + +