《化工热力学》课程教学课件（英文讲稿）流体热力学性质 Thermodynamic properties of fluids

Chapter 6 Thermodynamic properties of fluids

Chapter 6 Thermodynamic properties of fluids

6.1 property Relations for Homogeneous Phase 6.2 Residual Properties 6.3 Residual Properties by Equations of State 6.4 Two-phase systems 6.5 Thermodynamic Diagrams 6.6 Tables of Thermodynamic Properties 6.7 Generalized Property Correlations for Gases

6.1 property Relations for Homogeneous Phase 6.2 Residual Properties 6.3 Residual Properties by Equations of State 6.4 Two-phase systems 6.5 Thermodynamic Diagrams 6.6 Tables of Thermodynamic Properties 6.7 Generalized Property Correlations for Gases

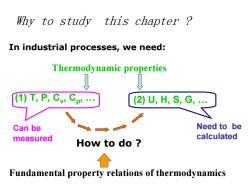
Why to study this chapter？ In industrial processes,we need: Thermodynamic properties T,P,Cv:Cp' (2)U,H,S,G Can be Need to be measured calculated How to do Fundamental property relations of thermodynamics

Why to study this chapter ? In industrial processes, we need: Thermodynamic properties (1) T, P, C v, C p, . (2) U, H, S, G, . How to do ? Can be measured Need to be calculated Fundamental property relations of thermodynamics

·学习化工热力学的目的在于应用，主要的应用就是热 力学性质的推算。 ·本章的主要任务就是将纯物质和均相定组成混合物系 统的一些有用的热力学性质表达成为能够直接测定的p、 V、T及C,*(理想气体热容)的普遍化函数，再结合 状态方程和C,*模型，就可以得到从p、V、T推算其它 热力学性质的具体关系式。即可以实现由一个状态方 程和理想气体热容模型推算其它热力学性质

• 学习化工热力学的目的在于应用，主要的应用就是热 力学性质的推算。 • 本章的主要任务就是将纯物质和均相定组成混合物系 统的一些有用的热力学性质表达成为能够直接测定的p、 V、T及Cp*（理想气体热容）的普遍化函数，再结合 状态方程和Cp*模型，就可以得到从p、V、T推算其它 热力学性质的具体关系式。即可以实现由一个状态方 程和理想气体热容模型推算其它热力学性质

6 Thermodynamic properties of fluids 6.1 property Relations for Homogeneous Phase 6.2 Residual Properties 6.3 Residual Properties by Equations of State 6.4 Two-phase systems 6.5 Thermodynamic Diagrams 6.6 Tables of Thermodynamic Properties 6.7 Generalized Property Correlations for Gases

6.1 property Relations for Homogeneous Phase 6.2 Residual Properties 6.3 Residual Properties by Equations of State 6.4 Two-phase systems 6.5 Thermodynamic Diagrams 6.6 Tables of Thermodynamic Properties 6.7 Generalized Property Correlations for Gases 6 Thermodynamic properties of fluids

6.1 property Relations for Homogeneous Phase 6.1.1 Fundamental Property Relations of Thermodynamics for Homogeneous Phase System For a homogeneous fluid of constant composition. (to one mole or to a unit mass) dU Tds-Pdv dH TdS +VdP Fundamental property relations dA=-Pdv-SdT dG=VdP-SdT

6.1 property Relations for Homogeneous Phase 6.1.1 Fundamental Property Relations of Thermodynamics for Homogeneous Phase System For a homogeneous fluid of constant composition. (to one mole or to a unit mass ) dU TdS PdV dH TdS VdP dA PdV SdT dG VdP SdT = − = + =− − = − Fundamental property relations

Attention Constant-compositon Constant-mass 四个 小方程式，是我 用到的微分方程， 使用些方程时之安注意以下几点： 1.恒组分、恒质量体系，也就是封闭体系； 2.均相体系（单相1 Homogeneous phase 3.平衡态间的变化； Closed 4.常用于1摩尔时的性顶 system Change from one equalibrium state from to another cumoHhrium stoto

Attention ! Constant - compositon Homogeneous phase Closed system Constant - mass Change from one equalibrium state from to another equalibrium state

6.1.2 The Criterion of Exactness for a Differential Expression Attention: F,x,y are all point function, and F is the continuous function about x,y IfF=F(,y以 M= Then the total differential of F is defined as: &x OF dF ay M N OM Oyox or dF=Mdx+Ndy O"F ayox =-1

6.1.2 The Criterion of Exactness for a Differential Expression If F= F (x, y) y x F F dF dx dy x y ⎛ ⎞ ∂ ∂⎛ ⎞ = + ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ ∂ ∂ ⎝ ⎠ dF Mdx Nd = + y Then the total differential of F is defined as： or 2 2 x y M F y y x N F x y x ⎛ ⎞ ∂ ∂ ⎜ ⎟ = ⎝ ⎠ ∂ ∂ ∂ ⎛ ⎞ ∂ ∂ ⎜ ⎟ = ⎝ ⎠ ∂ ∂ ∂ x y x N y M ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∂ ∂ = ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∂ ∂ y x F M x F N y ⎛ ⎞ ∂ = ⎜ ⎟ ⎝ ⎠ ∂ ⎛ ⎞ ∂ = ⎜ ⎟ ⎝ ⎠ ∂ M N 1 y x F Fx y xyF ⎛⎞ ⎛⎞ ∂∂∂ ⎛ ⎞ ⎜⎟ ⎜⎟ ⎜ ⎟ = − ⎝⎠ ⎝⎠ ∂∂∂ ⎝ ⎠ Attention: F, x, y are all point function, and F is the continuous function about x, y #

dF =Mdx Ndy aN 用于判断dF是否是全微分，也即判断F 是否是系统的状态函数 dF是全微分，数学上，F是点函数， 在热力学上，F是系统的状态函数

x y x N y M ⎟⎠⎞ ⎜⎝⎛ ∂∂ = ⎟⎟⎠⎞ ⎜⎜⎝⎛ ∂∂ dF Mdx Nd = + y 用于判断 dF 是否是全微分,也即判断F 是否是系统的状态函数 dF 是全微分，数学上，F是点函数， 在热力学上，F 是系统的状态函数

Example 证明热力学第一定律方程式6Q=dU+PdV 中的Q不是系统的状态函数 Solution For a single phase and single component f=C-P+2=1-1+2=2 Let U=U(T,V) U is state function -p. dU-?dU=TdS-Pdy d7+( U aU δQ=Mdx+Wdy

Example 证明热力学第一定律方程式 δQ U PV = d d + 中的Q不是系统的状态函数 Solution For a single phase and single component f = C-P+2 = 1-1+2=2 Let U=U(T, V) d () () v T U U U dT dV T V ∂ ∂ = + ∂ ∂ ( ) [( ) ( ) ] ) ( v T v T U dV PdV U Q dT T U dT V U d T P V V δ ∂ + ∂ ∂ + ∂ = + ∂ ∂ + ∂ = ∂ U is state function δQ Mdx Nd = + y dU=? dU=TdS-PdV ?