《信号与系统》课程教学课件（PPT讲稿）第四章 拉鲁拉斯变换、连续时间系统的S域分析（1/2）

第4章拉普拉斯变换、连续系统的 S域分析 4.1引言 4.2拉普拉斯变换的定义、收敛域 4.3拉普拉斯变换的基本性质 4.4拉普拉斯逆变换 4.5用拉普拉斯变换法分析电路、s域的元件模型 4.6系统函数H(s) 4.7系统函数的零、极点分布决定时域特性 4.8系统函数的零、极点分布决定频域特性 4.10全通网络和最小相移函数的零极点分布 4.11线性系统的稳定性

1 第4章 拉普拉斯变换、连续系统的 S域分析 4.1 引言 4.2 拉普拉斯变换的定义、收敛域 4.3拉普拉斯变换的基本性质 4.4拉普拉斯逆变换 4.5用拉普拉斯变换法分析电路、s域的元件模型 4.6系统函数H(s) 4.7系统函数的零、极点分布决定时域特性 4.8系统函数的零、极点分布决定频域特性 4.10全通网络和最小相移函数的零极点分布 4.11线性系统的稳定性

4.1引言 拉普拉斯变换是分析连续信号与系统的一种好方法。 线性时不变系统方法的回顾： 时域分析法：卷积积分—只能求解零状态响应 变换域分析法：傅氏变换分析法：思想方法是把时 间变量函数变换到变换域中的某一变量的函数。 分析的实质： ()是将激励信号分解成某种基本的单元信号； (2)求基本单元信号通过系统的响应； (3)最后叠加起来求得总的响应

4.1 引言 2 拉普拉斯变换是分析连续信号与系统的一种好方法。 线性时不变系统方法的回顾： 时域分析法：卷积积分——只能求解零状态响应 变换域分析法：傅氏变换分析法：思想方法是把时 间变量函数变换到变换域中的某一变量的函数。 分析的实质： (1)是将激励信号分解成某种基本的单元信号； (2)求基本单元信号通过系统的响应； (3)最后叠加起来求得总的响应

卷积分析法的单元信号是冲激函数；傅氏变换分 析法的单元信号是虚指函数。它们之间的桥梁是傅 氏变换的时域卷积定理。 傅氏变换分析法的优点：物理意义明确，也是信号 分析的有效工具。 傅氏变换的不足：(1)要求信号满足狄里赫利条件（满 足绝对可积条件)。使一般周期信号，阶跃函数等只能 虽借助于广义函数求得傅氏变换，由于频域中出现冲 激函数，使计算带来困难；(2)求傅氏反变换有时比较 麻烦；(3)只能求解零状态响应

3 卷积分析法的单元信号是冲激函数；傅氏变换分 析法的单元信号是虚指函数。它们之间的桥梁是傅 氏变换的时域卷积定理。 傅氏变换分析法的优点：物理意义明确，也是信号 分析的有效工具。 傅氏变换的不足：(1)要求信号满足狄里赫利条件(满 足绝对可积条件)。使一般周期信号，阶跃函数等只能 虽借助于广义函数求得傅氏变换，由于频域中出现冲 激函数，使计算带来困难；(2)求傅氏反变换有时比较 麻烦； (3)只能求解零状态响应

下面将介绍拉普拉斯变换（简称拉氏变换) 它的定义方法有很多，这里为了强化它的物理意义， 可以看作一种广义的傅氏变换。将频域扩展为复频域。 拉氏变换的优点： 1)求解简化； 2)把微分、积分方程转化为代数方程； 3)将复杂函数转化为简单的初等函数； 4)将卷积转化为乘法运算

4 拉氏变换的优点： 1）求解简化； 2）把微分、积分方程转化为代数方程； 3）将复杂函数转化为简单的初等函数； 4）将卷积转化为乘法运算。 下面将介绍拉普拉斯变换（简称拉氏变换） 它的定义方法有很多，这里为了强化它的物理意义， 可以看作一种广义的傅氏变换。将频域扩展为复频域

4炽射普瘦捻的腚义、收敛域 信号不满足绝对可积条件的原因是 当t→o或t→-oo时，f(t)不趋于零。 若f(t)不满足狄里赫利条件，我们为了能获得变换域 中的函数，人为地用一个实指函数eo1去乘f(t)。 只要σ取得合适，很多函数（几乎所有常用的函数） 都可以满足绝对可积的条件。 称o为衰减因子；称eo为收敛因子

4.2 拉普拉斯变换的定义、收敛域 5 一、 从傅氏变换到拉氏变换 信号不满足绝对可积条件的原因是 当t → 或t → −时，f (t)不趋于零。 若 不满足狄里赫利条件，我们为了能获得变换域 中的函数，人为地用一个实指函数 去乘 。 f (t) e f (t) − t 称  为衰减因子；称 e − t 为收敛因子。 只要  取得合适，很多函数(几乎所有常用的函数) 都可以满足绝对可积的条件

求f(t)eo的傅氏变换： FTIf(t)e"]=[f(t)e-"e-dt =[f(t)e-dt 它是o+jo的函数，记o+j0=s为复频率 显然，可表示成F(o+jo)=∫f(t)eo+o'dt 记为 F(s)=[f(t)e-"dt FT[f(t)ea]=F(s)=f(t)e"dt

6 =   − − − − f t e f t e e dt t t jt F T[ ( ) ] ( )   − − + = f t e dt ( j )t ( )   它 是 + j的函数，记 + j = s为复频率 1、 求 f t e 的傅氏变换： t ( ) − 显然，可表示成 F( j ) f t e dt j t     + = − + −   ( ) ( ) =   − − F s f t e dt s t 记为 ( ) ( ) = =   − − − f t e F s f t e dt t s t [ ( ) ] ( ) ( )  F T

FTIf(t)e"]=F(s)=ff(t)edt 其反变换.为f0e”F(oe”dn e“不是o的函数，故-2元了rs)eota"dn F(s)=[f(t)e"dt 2 上两式称一对拉普拉斯变换式，正变换、反变换。 F(s)=L[f(t)],f(t)=L[F(s)] f(t)←→F(s) 拉氏变换扩大了信号的变换范围

7   − − =     f t e F s e d t j t ( ) 2 1 ( )   − + =       e f t F s e d t ( j )t ( ) 2 1 不 是 的函数，故 ( ) =   − − F s f t e dt s t ( ) ( ) 上两式称一对拉普拉斯变换式，正变换、反变换。 其反变换，为 f t ( ) j F s e d s s t j j ( )= −  +   1 2   F(s) [ f (t)], f (t) [F(s)] - 1 记 = L = L f (t)  F(s) 拉氏变换扩大了信号的变换范围。 = =   − − − f t e F s f t e dt t s t [ ( ) ] ( ) ( )  F T

拉普拉斯变换与傅里叶变换的区别厅 FT: 时域函数f) 频域函数F(o) 变量t 变量0 (变量t、o都是实数) LT: 时域函数f) 复频域函数F(s) 变量t 变量s(复频率) t（实数) S=0+j0(复数) 即：傅里叶变换建立了时域与频域之间的联系； 拉普拉斯变换建立了时域与复频域之间的联系

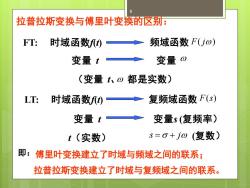
8 拉普拉斯变换与傅里叶变换的区别： FT: 时域函数f(t) 频域函数 F( j) 变量 t 变量  LT: 时域函数f(t) 复频域函数 F(s) （变量 t、  都是实数） 变量 t 变量s(复频率） t（实数） s = + j (复数） 即：傅里叶变换建立了时域与频域之间的联系； 拉普拉斯变换建立了时域与复频域之间的联系

2、单边拉氏变换 由于1.实际信号都是有始信号，即t<0时，f(t)=0 或者只需考虑t≥0的部分；2.我们观察问题总有一个 起点。此时 F(s)=f(t)e-"dt 积分下限用0目的是把=0时出现的冲激包含进去， 这样，利用拉氏变换求解微分方程时，可以直接引用 已知的初始状态f(0),但反变换的积分限并不改变。 以后重点讨论单边拉氏变换

2、 单边拉氏变换 9 由于1.实际信号都是有始信号，即 t  0时，f (t) = 0 或者只需考虑 的部分；2.我们观察问题总有一个 起点。此时 t  0 =   − − 0 F(s) f (t)e dt s t 积分下限用 目的是把 时出现的冲激包含进去， 这样，利用拉氏变换求解微分方程时，可以直接引用 已知的初始状态 ，但反变换的积分限并不改变。 0 − t = 0 f (0 − ) 以后重点讨论单边拉氏变换

10 由于我们重点讨论单边拉氏变换，所以有f(t)和f(t)u(t) 的拉氏正变换F(s)是一样的。 反之，已知F(s)求拉氏反变换式，也无法求得到<0 时的f()表达式。 如1和u(t)的拉氏变换是一样的。 单边拉氏变换的优点： ()不仅可以求解零状态响应，而且可以求解零输入 响应或全响应

10 由于我们重点讨论单边拉氏变换，所以有 和 的拉氏正变换 是一样的。 f (t) f (t)u(t) F(s) 反之，已知 求拉氏反变换式，也无法求得到 时的 表达式。 F(s) f (t) t  0 如 1 和 u(t) 的拉氏变换是一样的。 单边拉氏变换的优点： (1)不仅可以求解零状态响应，而且可以求解零输入 响应或全响应