石河子大学：《化工机械设备基础》课程教学资源（PPT课件）第2章 拉伸、压缩与剪切

物体的受力分析和静力平衡方程《化工机械设备基础》第一章第二章拉伸、压缩与剪切CG◆研究方向：材料力学研究对象：变形体变形体假设：传动轴1.连续性假设2.均匀性假设3.各向同性假设4.小变形假设扭转变形特点2025年6月10日夏期二返回目景石河子大学化学化工学院

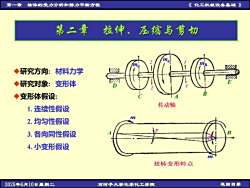
第一章 物体的受力分析和静力平衡方程 《 化工机械设备基础 》 2025年6月10日星期二 石河子大学化学化工学院 返回目录 第二章 拉伸、压缩与剪切 ◆研究方向: 材料力学 ◆研究对象: 变形体 ◆变形体假设: 1. 连续性假设 2. 均匀性假设 3. 各向同性假设 4. 小变形假设

第一章物体的受力分析和静力平衡方程《化工机械设备基础》如果构件的长度比横向尺寸大得多，这样的构件就称为杆件杆件的各个横截面形心的连线称为轴线。如果杆的轴线是直线，而且各横截面都相等，就称为等截面杆（图a）。除此以外还有变截面直杆、曲杆（图b，c）等如果构件的厚度比起它的长和宽两个方向的尺寸小得多，这样的构件就称为薄板或壳（图d，e），例如锅炉和化工容器等(c)(e)(b)(d)2025年6月10日夏期二石河子大学化学化工学院送回目景

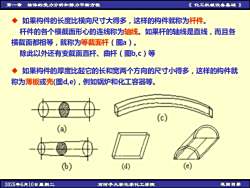
第一章 物体的受力分析和静力平衡方程 《 化工机械设备基础 》 2025年6月10日星期二 石河子大学化学化工学院 返回目录 ◆ 如果构件的长度比横向尺寸大得多，这样的构件就称为杆件。 杆件的各个横截面形心的连线称为轴线。如果杆的轴线是直线，而且各 横截面都相等，就称为等截面杆（图a）。 除此以外还有变截面直杆、曲杆（图b,c）等 ◆ 如果构件的厚度比起它的长和宽两个方向的尺寸小得多，这样的构件就 称为薄板或壳(图d,e)，例如锅炉和化工容器等

物体的受力分析和静力平衡方程《化工机械设备基础》第一章第一节多轴向拉伸与压缩的概念和实例工程实际中直杆拉伸和压缩的实例是很多的。例如起吊设备时的绳索和连接容器法兰用的螺栓，它们所受的作用力都是拉伸的实例；容器的立式支腿和干斤顶的螺杆，则是受压缩的构件。2025年6月10日里期二返回目景石河子大学化学化工学院

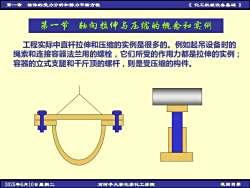
第一章 物体的受力分析和静力平衡方程 《 化工机械设备基础 》 2025年6月10日星期二 石河子大学化学化工学院 返回目录 第一节 轴向拉伸与压缩的概念和实例 工程实际中直杆拉伸和压缩的实例是很多的。例如起吊设备时的 绳索和连接容器法兰用的螺栓，它们所受的作用力都是拉伸的实例； 容器的立式支腿和千斤顶的螺杆，则是受压缩的构件

第一章物体的受力分析和静力平衡方程《化工机械设备基础》拉伸和压缩时的受力特点是：沿着杆件的轴线方向作用一对大小相等、方向相反的外力。当外力背离杆件时称为轴向拉伸，外力指向杆件时称为轴向压缩拉伸和压缩时的变形特点是：拉伸时杆件沿轴向伸长，横向尺寸缩小：压缩时杆件沿轴向缩短，横向尺寸增大。轴向拉伸轴向压缩P2025年6月10日夏期二石河子大学化学化工学院送回目景

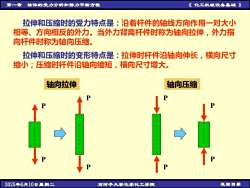
第一章 物体的受力分析和静力平衡方程 《 化工机械设备基础 》 2025年6月10日星期二 石河子大学化学化工学院 返回目录 拉伸和压缩时的受力特点是：沿着杆件的轴线方向作用一对大小 相等、方向相反的外力。当外力背离杆件时称为轴向拉伸，外力指 向杆件时称为轴向压缩。 拉伸和压缩时的变形特点是：拉伸时杆件沿轴向伸长，横向尺寸 缩小；压缩时杆件沿轴向缩短，横向尺寸增大。 P P 轴向拉伸 轴向压缩 P P P P P P

物体的受力分析和静力平衡方程《化工机械设备基础》第一章第二节轴向拉伸或压缩时横截面上的内力内力的概念物体在未受外力作用时，组成物体的分子之间本来就存在相互作用的力。受外力作用后物体内部相互作用力的情况要发生变化，同时物体要产生变形，这种由外力引起的物体内部相互作用力的变化量称为附加内力，简称内力。物体的变形及破坏情况与内力有着密切的联系，因而在分析构件的强度与刚度问题时，要从分析内力入手。2025年6月10日夏期二返回目景石河子大学化学化工学院

第一章 物体的受力分析和静力平衡方程 《 化工机械设备基础 》 2025年6月10日星期二 石河子大学化学化工学院 返回目录 物体在未受外力作用时，组成物体的分子之间本来就存在相互作用 的力。 受外力作用后物体内部相互作用力的情况要发生变化，同时物体要 产生变形，这种由外力引起的物体内部相互作用力的变化量称为附加内 力，简称内力。 物体的变形及破坏情况与内力有着密切的联系，因而在分析构件的 强度与刚度问题时，要从分析内力入手。 第二节 轴向拉伸或压缩时横截面上的内力 一、内力的概念

第一章物体的受力分析和静力平衡方程《化工机械设备基础》研究下图所示的杆件AB，它在外力的作用下处于平衡状态。为了计算内力，假想用一垂直于杆体轴线的m-n平面将杆截开，分成C、D两部分。N=N'-P4区分内力的性质应该依据变形，所以通常规定：N伴随拉伸变形产生的内力取正值；mnN伴随压缩变形产生的内力取负值为了区分杆件在发生不同变形时（拉压、弯、剪、扭)所产生的内力，我们把B由于拉伸或压缩变形而产生的横截面上P的内力称为轴力，用N表示。BP2025年6月10日夏期二石河子大学化学化工学院送回目景

第一章 物体的受力分析和静力平衡方程 《 化工机械设备基础 》 2025年6月10日星期二 石河子大学化学化工学院 返回目录 研究下图所示的杆件AB，它在外力的作用下处于平衡状态。为了计算内 力，假想用一垂直于杆体轴线的m-n平面将杆截开，分成C、D两部分。 N = N' = P 区分内力的性质应该依据变形，所以 通常规定： 伴随拉伸变形产生的内力取正值； 伴随压缩变形产生的内力取负值。 为了区分杆件在发生不同变形时(拉、 压、弯、剪、扭)所产生的内力，我们把 由于拉伸或压缩变形而产生的横截面上 的内力称为轴力，用N 表示。 P P m n A B P A P B N N

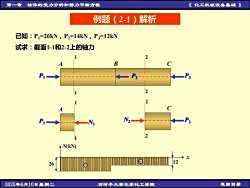
物体的受力分析和静力平衡方程《化工机械设备基础》第一章例题（2-1）解析已知:P=26kN,P2-14kN,P3=12kN试求：截面1-1和2-2上的轴力BPPP212N2P3PN+N(kN)262025年6月10日夏期二返回目景石河子大学化学化工学院

第一章 物体的受力分析和静力平衡方程 《 化工机械设备基础 》 2025年6月10日星期二 石河子大学化学化工学院 返回目录 已知：P1=26kN，P2=14kN，P3=12kN 试求：截面1-1和2-2上的轴力 例题（2-1）解析 P1 P2 P3 A B C 1 1 2 2 P1 A 1 1 N1 P3 C 2 2 N2 N(kN) 26 12 x

《化工机械设备基础》第一章物体的受力分析和静力平衡方程用截面法求内力的步骤可归纳如下：1.在需要求内力处假想用一横截面将构件截开，分成两部分：2。以任一部分为研究对象；3。在截面上加上内力，以代替另一部分对研究对象的作用；4写出研究对象的平衡方程式，解出截面上的内力。凡是使该截面产生拉伸轴力的外力取正值：凡是使该截面产生压缩轴力的外力取负值。所得内力的计算结果若为正，则表示该截面上作用的是拉伸轴力：结果为负，则表示该截面上作用的是压缩轴力。回目景2025年6月10日夏期二石河子大学化学化工学院

第一章 物体的受力分析和静力平衡方程 《 化工机械设备基础 》 2025年6月10日星期二 石河子大学化学化工学院 返回目录 用截面法求内力的步骤可归纳如下： 1. 在需要求内力处假想用一横截面将构件截开，分成两部分； 2．以任一部分为研究对象； 3．在截面上加上内力，以代替另一部分对研究对象的作用； 4．写出研究对象的平衡方程式，解出截面上的内力。 凡是使该截面产生拉伸轴力的外力取正值； 凡是使该截面产生压缩轴力的外力取负值。 所得内力的计算结果若为正，则表示该截面上作用的是拉伸轴 力；结果为负，则表示该截面上作用的是压缩轴力

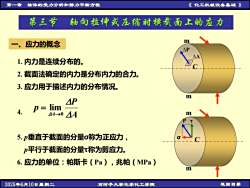
物体的受力分析和静力平衡方程《化工机械设备基础》第一章第三节轴向拉伸或压缩时横截面上的应力m应力的概念APAA1.内力是连续分布的。2.截面法确定的内力是分布内力的合力。3.应力用于描述内力的分布情况。m4Pp= lim4.44-0 4AmPT15.p垂直于截面的分量o称为正应力，p平行于截面的分量t称为剪应力。6.应力的单位：帕斯卡（Pa），兆帕（MIPa）m2025年6月10日夏期二返回目景石河子大学化学化工学院

第一章 物体的受力分析和静力平衡方程 《 化工机械设备基础 》 2025年6月10日星期二 石河子大学化学化工学院 返回目录 第三节 轴向拉伸或压缩时横截面上的应力 一、应力的概念 1. 内力是连续分布的。 2. 截面法确定的内力是分布内力的合力。 3. 应力用于描述内力的分布情况。 4. 5. p垂直于截面的分量σ称为正应力， p平行于截面的分量τ称为剪应力。 6. 应力的单位：帕斯卡（Pa），兆帕（MPa） m m ∆P ∆A C m m P τ C σ A P p A    0 lim → =

第一章物体的受力分析和静力平衡方程《化工机械设备基础》二、轴向拉伸（压缩）时横截面上的应力平面假设：杆件变形前的各横截面在变形后仍保持为平面且垂直于杆的轴线aPP5SdbdaN=TodA=oANUO（正负号与轴力N相同）A2025年6月10日夏期二石河子大学化学化工学院送回目景

第一章 物体的受力分析和静力平衡方程 《 化工机械设备基础 》 2025年6月10日星期二 石河子大学化学化工学院 返回目录 二、轴向拉伸（压缩）时横截面上的应力 a c b d a' c ' b' d ' P P P N σ 平面假设： 杆件变形前的各横截面在变形后仍保持为平面且垂直于杆的轴线。 A N N dA A A  = = =     （正负号与轴力N相同）