内蒙古科技大学：《材料成型控制工程基础》课程授课教案（讲义）第3章 PID控制及其调节过程

内 蒙古科技大学教案 材料与冶金学院李振亮 课程名称：《材料成型控制工程基础》（第3章，共11章） 编写时间：2010年8月29日 3.PD控制及其调节过程 授课章节 3.1PID控制概述3.2PID调节规律3.3PID调节规律对系统过渡过程的影响 3.4PD调节器参数的工程整定3.5加热炉PD温度控制的MATLAB仿真 目的要求 本章内容属于古典控制策略的研究范球，主要介绍PD控制器的特点、调节规律，调节规 律对系统动态过程的影响，以及如何对PID控制器中的参数进行整定等内容。 重点：①ID控制的优点。②比例带的概念及其对调节过程的影响。③不同调节规律的特 重点难点 点。④调节器中不同调节作用的曲线比较。 难点：⑤PID控制器的参数整定。 3.PID控制及其调节过程 3.1PD控制概述 在PD调节规律基础上发展出的PD控制是古典控制策略的一种，其控制原理是 种负反馈控制。 PID( ona ntegrate-)控制是比例、积分、微分控制的简称。上个 世纪40年代以前，在工业生产过程控制中，除了最简单的开关控制外，它是唯一的控制 掌握（考点） 方式。从20世纪50年代开始，PID控制开始应用，并在模拟控制和数字控制系统中已 形成了成熟的算法。据介绍，直到现在90%以上的工业控制回路仍采用各种形式的PD 控制。 PD控制之所以应用数十年而未被淘汰，是因为它具有一系列优良的性质： ()原理简单，使用方便。PD控制由P、【、D三个环节的不同组合而成，其基本组 成原理比较简单，参数的物理意义比较明确。 PID算法整合了系统动态过程中的过去、现在和将来的信息。其中比例(P)代表当 前的信息，起纠正偏差的作用，使被控系统反应迅速：积分()代表过去积累的信息， 只有通过积分作用，才能消除系统的静态误差，改善系统的静态特性：微分(D)代表 对系统将来的预测信息，在信号变化时有超前控制作用，有利于减小超调、克服振荡、 加快系统的过渡过程。 (2)适应性强。可广泛应用于化工、热工、治金、炼油及造纸和建材等各种生产部门 按PD控制原理进行工作的自动调节器早已商品化，在具体实现上它们经历了机械式、 液动式、气动式、电子式等发展过程，但始终没有脱离PID控制的范畴。即使目前最新 式的过程控制计算机，其基本控制功能也仍然是PD控制。 (3)鲁棒性(robustness)强，其控制品质对被控对象的变化不太敏感，非常适用于环 境恶劣的工业生产现场。所谓鲁棒性，指在存在扰动和未建模动态条件下，也就是系统 的实际动态与应用数学模型之间误差较大时，系统仍能保持稳定性，基本维持原有设计 中控制性能的能力。 它的研究可以从“稳定鲁棒性”和“性能鲁棒性”两方面来区分

1 内 蒙 古 科 技 大 学 教 案 材 料 与 冶 金 学 院 李 振 亮 课程名称：《材料成型控制工程基础》 （第 3 章，共 11 章） 编写时间：2010 年 8 月 29 日 授课章节 3. PID 控制及其调节过程 3.1 PID 控制概述 3.2 PID 调节规律 3.3 PID 调节规律对系统过渡过程的影响 3.4 PID 调节器参数的工程整定 3.5 加热炉 PID 温度控制的 MATLAB 仿真 目的要求 本章内容属于古典控制策略的研究范畴，主要介绍 PID 控制器的特点、调节规律，调节规 律对系统动态过程的影响，以及如何对 PID 控制器中的参数进行整定等内容。 重点难点 重点： ①PID 控制的优点。②比例带的概念及其对调节过程的影响。③不同调节规律的特 点。④调节器中不同调节作用的曲线比较。 难点： ⑤PID 控制器的参数整定。 3. PID 控制及其调节过程 3.1 PID 控制概述 在 PID 调节规律基础上发展出的 PID 控制是古典控制策略的一种，其控制原理是一 种负反馈控制。 PID（proportional-integrate-differential）控制是比例、积分、微分控制的简称。上个 世纪 40 年代以前，在工业生产过程控制中，除了最简单的开关控制外，它是唯一的控制 方式。从 20 世纪 50 年代开始，PID 控制开始应用，并在模拟控制和数字控制系统中已 形成了成熟的算法。据介绍，直到现在 90％以上的工业控制回路仍采用各种形式的 PID 控制。 PID 控制之所以应用数十年而未被淘汰，是因为它具有一系列优良的性质： (1)原理简单，使用方便。PID 控制由 P、I、D 三个环节的不同组合而成，其基本组 成原理比较简单，参数的物理意义比较明确。 PID 算法整合了系统动态过程中的过去、现在和将来的信息。其中比例（P）代表当 前的信息，起纠正偏差的作用，使被控系统反应迅速；积分（I）代表过去积累的信息， 只有通过积分作用，才能消除系统的静态误差，改善系统的静态特性；微分（D）代表 对系统将来的预测信息，在信号变化时有超前控制作用，有利于减小超调、克服振荡、 加快系统的过渡过程。 (2)适应性强。可广泛应用于化工、热工、冶金、炼油及造纸和建材等各种生产部门。 按 PID 控制原理进行工作的自动调节器早已商品化，在具体实现上它们经历了机械式、 液动式、气动式、电子式等发展过程，但始终没有脱离 PID 控制的范畴。即使目前最新 式的过程控制计算机，其基本控制功能也仍然是 PID 控制。 (3)鲁棒性（robustness）强，其控制品质对被控对象的变化不太敏感，非常适用于环 境恶劣的工业生产现场。所谓鲁棒性，指在存在扰动和未建模动态条件下，也就是系统 的实际动态与应用数学模型之间误差较大时，系统仍能保持稳定性，基本维持原有设计 中控制性能的能力。 它的研究可以从“稳定鲁棒性”和“性能鲁棒性”两方面来区分。 掌握（考点）

内蒙古科技大学教案 (4)PID算法有一套完整的参数整定与设计方法，易于被工程技术人员掌握。 5许多工 业回路中对控制快速性和控制精度要求不是很高，而更重视系统的可靠性 时，使用PID控制能获得较高的性价比。 在过程控制应用中，人们首先想到的总是PD控制，一个大型现代化生产装置的控 制回路可能多达一两百种甚至更多，但其中绝大部分都采用PD控制。当被控制对象易 于控制而控制要求不高时，可采用更简单的开关控制：当被控对象难以控制而控制要求 又特别高，这时如果 PD控制难以达到要求，可以考虑采用更先进的控制方法。 (⑥)长期应用过程中，对PD算法缺陷可以进行改良。例如：为克服微分带米的高频 干扰，采用带滤波的PD控制：为克服大偏差带来的积分饱和及超调现象，可采用积分 分离的PD控制：为补偿被控系统的非线性因素，采用可变增益的PD控制等等。 3.2PID调节规律 在过程控制系统的组成中我们知道，控制器，又称“调节器”，（或“自动调节器” 是过程自动调节中不可缺少的一个环节，它将输出量检测值y)与设定值【进行比较(A ©)，然后由调节器按照一定的控制算出输出控制量△u。如果从调节系统中取出一个调节 器，它的作用如图3-1所示。 偏差信号△调节器输出信号△9 图31调节器的输入和输出信号 图中△为偏差信号，习惯上常以偏差在测量仪表全量程中所占的百分数表示： c=测量值-给定值×100% 测量范围 例如：测量范围为0~1100℃，设定温度为980℃，若测量温度为969℃，则偏差信号 为 △e=(969-980)/1100=-1.0% 调节器输出与偏差信号之间的函数关系称为调节规律。调节规律是决定调节器特性 的。在调节器输出稳定之前，偏差△©与输出之间的相互关系，称为调节器的动态特性。 重点（考点） 在调节器上施加恒定的偏差，经过相当长的时间，输出稳定以后，偏差△与输出的相 互关系称为调节器的静态 性 在研究调节器的动态特性时，一般假定：若偏差有一阶跃变化△©，输出u随时间 而变化的增量为△u,△u与△e的函数关系即决定了调节器的调节规律。 常用的调节器规律有许多种，如两位式调节规律、比例调节规律、积分山调节 规律，徽分D调节规、比例积分通节规律、比剑分P心调节规律、比侧积分徽 分D)调节规律 3.2.1双位调节 双位调节器结构简单使用方便、价格便宜，在电阻加热设备的温度调节方面可以 节省电能，故应用很普遍

2 内 蒙 古 科 技 大 学 教 案 (4)PID 算法有一套完整的参数整定与设计方法，易于被工程技术人员掌握。 (5)许多工业回路中对控制快速性和控制精度要求不是很高，而更重视系统的可靠性 时，使用 PID 控制能获得较高的性价比。 在过程控制应用中，人们首先想到的总是 PID 控制，一个大型现代化生产装置的控 制回路可能多达一两百种甚至更多，但其中绝大部分都采用 PID 控制。当被控制对象易 于控制而控制要求不高时，可采用更简单的开关控制；当被控对象难以控制而控制要求 又特别高，这时如果 PID 控制难以达到要求，可以考虑采用更先进的控制方法。 (6)长期应用过程中，对 PID 算法缺陷可以进行改良。例如：为克服微分带来的高频 干扰，采用带滤波的 PID 控制；为克服大偏差带来的积分饱和及超调现象，可采用积分 分离的 PID 控制；为补偿被控系统的非线性因素，采用可变增益的 PID 控制等等。 3.2 PID 调节规律 在过程控制系统的组成中我们知道，控制器，又称“调节器”，（或“自动调节器”） 是过程自动调节中不可缺少的一个环节，它将输出量检测值 y(t)与设定值 r 进行比较（△ e）,然后由调节器按照一定的控制算出输出控制量△u。如果从调节系统中取出一个调节 器，它的作用如图 3-1 所示。 图 3-1 调节器的输入和输出信号 图中△e 为偏差信号，习惯上常以偏差在测量仪表全量程中所占的百分数表示： 100% −  = 测量范围 测量值 给定值 e 例如：测量范围为 0～1100℃,设定温度为 980℃，若测量温度为 969℃，则偏差信号 为： e = (969 − 980)/1100 = −1.0% 调节器输出与偏差信号之间的函数关系称为调节规律。调节规律是决定调节器特性 的。在调节器输出稳定之前，偏差△e 与输出之间的相互关系，称为调节器的动态特性。 在调节器上施加恒定的偏差，经过相当长的时间，输出稳定以后，偏差△e 与输出的相 互关系称为调节器的静态特性。 在研究调节器的动态特性时，一般假定：若偏差有一阶跃变化△e，输出 u 随时间 而变化的增量为△u，△u 与△e 的函数关系即决定了调节器的调节规律。 常用的调节器规律有许多种，如两位式调节规律、比例(P)调节规律、积分(I)调节 规律、微分(D)调节规律、比例积分(PI)调节规律、比例微分(PD)调节规律、比例积分微 分(PID)调节规律。 3.2.1 双位调节 双位调节器结构简单﹑使用方便、价格便宜，在电阻加热设备的温度调节方面可以 节省电能，故应用很普遍。 重点（考点） 偏差信号 Δe 调节器 输出信号 Δu

内蒙古科技大学教案

3 内 蒙 古 科 技 大 学 教 案

3.22比例调节(P) 3.2.21动作过程 双位调节不可能使被调量稳定在给定数值，这是由于调节机构只按被调量偏差的方向来动作，而 且只有两个极限位置，不可能建立起能量或物流量的平衡，因而被调量也不能稳定。比例调节则慨 是按被调量偏差方向又按其大小成比例地改变调节机构的开度。 即偏差大，开度变化也大：偏差小， 开度变化也小。这样能量变化较为平稳，且最终可以达到能量或物料量的平衡，被调量也就能稳定 下来。 液面调节系统示意图见图32所示。其中，Q1为进料量，Q2为出料量，山为调节器阀门量度。 二←Q1 图3.2液面调节系统 我们可以用一个数学表达式来表示调节器的比例调节规律，由图3-2所示阀门与液柱之间是通 过杠杆来联 的 由相似三角形符出△uW△c=bA所以 AU-BAe-KAe (3-1) 式中： △U=U-U。 一一调节阀开度变化（即调节器的输出信号）方 △e=H-H 测量值与给定值的偏差（即调节器的输入）： 一一比例系数。 比例系数K即可以根据需要来调整调节作用的强弱，在图3-2中只要改变支点位置即可。 3.2.2.2比例调节的特 (1)作用快。比例调节一个很大的优点是反应快，无滞后。只要一有偏差，立即就有一个相应 的调节作用。它能及时克服扰动，使被调参数稳定在给定值附近。 (2)有余差（静差）。扰动（如负荷变化）出现后，比例调节的结果使被调量不能回到给定值 而只能恢复到给定值附近，因而有余差。 比例作用的强第用比例晶 (有时又称“比例喷6”、P的变窄即是 点（考 创度6的大小)来表小。比例度6的定义如下： 点 内蒙古科技大学教案

4 3.2.2 比例调节(P) 3.2.2.1 动作过程 双位调节不可能使被调量稳定在给定数值，这是由于调节机构只按被调量偏差的方向来动作，而 且只有两个极限位置，不可能建立起能量或物流量的平衡，因而被调量也不能稳定。比例调节则既 是按被调量偏差方向又按其大小成比例地改变调节机构的开度。即偏差大，开度变化也大；偏差小， 开度变化也小。这样能量变化较为平稳，且最终可以达到能量或物料量的平衡，被调量也就能稳定 下来。 液面调节系统示意图见图 3-2 所示。其中，Q1 为进料量，Q2 为出料量，u 为调节器阀门量度。 图 3-2 液面调节系统 我们可以用一个数学表达式来表示调节器的比例调节规律，由图 3-2 所示阀门与液柱之间是通 过杠杆来联系的，由相似三角形得出△u/△e＝b/a,所以 e K e a b U =   = p   （3-1） 式中： U =U −U0 ——调节阀开度变化（即调节器的输出信号）； H H0 e = − ——测量值与给定值的偏差（即调节器的输入）； a b Kp = ——比例系数。 比例系数 Kp 可以根据需要来调整调节作用的强弱，在图 3-2 中只要改变支点位置即可。 3.2.2.2 比例调节的特点 （1）作用快。比例调节一个很大的优点是反应快，无滞后。只要一有偏差，立即就有一个相应 的调节作用。它能及时克服扰动，使被调参数稳定在给定值附近。 （2）有余差（静差）。扰动（如负荷变化）出现后，比例调节的结果使被调量不能回到给定值， 而只能恢复到给定值附近，因而有余差。 （3)比例带（P） 在工业上，比例调节器比例作用的强弱常用比例带 P（有时又称“比例度 δ”，P 的宽窄即是表 示比例度 δ 的大小）来表示。比例度 δ 的定义如下： 重点（考 点） 内 蒙 古 科 技 大 学 教 案

×100以 (P-B)AP-P) △eZ=-Z×100% (3-2) AP/(P-P) 式中： △e=H-H。一—调节器的输入偏差： △P=P-R 调节器的相应输出变化： Z一Zn一一调节器输入的变化范围即仪表的量程： P-Pin 一一调节器输出的变化范围 5代表使节升度政变1006，从全关到全时所高的被调量的变1 通。只有当被调量处在这个范围以内，固节网的开度（变化）才与偏差成比例 上例度的名字也就由此而来的。超位个·比例带”以外，调节我已处于全关写 开的状态，此时节器的输出与输人已不再保持比例失系，而节器至少也国 比例带P习用它相对于被测仪表的鼠程的百分 怎示，所以，比例度。又可定义为：使硝节器的输出变化达到全最程《或全范圆 ,输人偏左改变了满量程的百分比。例如，当6一00%时，喻人改变了满量围 的100%，则输出也能校H例地改变其全范丽的100%：当ǒ=200%时，徐入男 %,换句说，即当输☑ 可见，δ大则调节作用就弱，ǒ小则调节作用就强。6的大小也可以用比例 带(P)的宽窄来表示：δ大则比例带(P)宽，6小则比例带(P)窄。 3.2.2.3比例调节的传递函数 比例调节器的传递函数为： (3-4) 其中Kp一一比例系数 比例调节器传递函数的方块图见图3-3所示。 图3-3比例调节器传递函数方块图 内蒙古科技大学教案

5 100% /( ) /( ) 100% ( )/( ) ( )/( ) max min max min 0 max min 0 max min   −  − =  − − − − = P P P e Z Z P P P P H H Z Z  （3-2） 式中： H H0 e = − ——调节器的输入偏差； P = P − P0 ——调节器的相应输出变化； Zmax − Zmin ——调节器输入的变化范围即仪表的量程； Pmax − Pmin ——调节器输出的变化范围。 δ 代表使调节阀开度改变 100％，即从全关到全开时所需要的被调量的变化 范围。只有当被调量处在这个范围以内，调节阀的开度（变化）才与偏差成比例， 比例度的名字也就由此而来的。超出这个“比例带”以外，调节阀已处于全关或 全开的状态，此时调节器的输出与输入已不再保持比例关系，而调节器至少也暂 时失去了其控制作用 实际上，调节器的比例带 P 习惯用它相对于被调量测量仪表的量程的百分数 表示，所以，比例度 δ 又可定义为：使调节器的输出变化达到全量程（或全范围） 时，输入偏差改变了满量程的百分比。例如，当 δ＝100％时，输入改变了满量程 的 100％，则输出也能按比例地改变其全范围的 100％；当 δ＝200％时，输入要 改变满量程的 200％时，输出才能够改变全范围的 100％；换句话说，即当输入 改变满量程的 100％时，输出只能改变其全范围的 50％。 可见，δ 大则调节作用就弱，δ 小则调节作用就强。δ的大小也可以用比例 带(P)的宽窄来表示：δ 大则比例带(P)宽，δ小则比例带(P)窄。 3.2.2.3 比例调节的传递函数 比例调节器的传递函数为： Kp E s U s G s = = ( ) ( ) ( ) （3-4） 其中 Kp ——比例系数 比例调节器传递函数的方块图见图 3-3 所示。 图 3-3 比例调节器传递函数方块图 内 蒙 古 科 技 大 学 教 案

3.2.3积分调节(D 3.2.3.1积分调节规律(1) 积分调节规律就是调节器的输出变化量与输入偏差随时间的积分成正比的调节规律， 亦即调节器输出的变化速度与输入偏差的大小成正比。所以只要有偏差，调节器给出的变 化速度就不等于零，当偏差为零时，输出就保持不变，而不管当时的阀位是多少。因此 调节器有差即动，无差则停。可见，积分作用是能消除余差的。 积分调节规律可用下式表示： (3-5) (重点，该部 分是考点) (3-6) 式中：K— 一积分速度 T一一积分时间 323,2积分时间 积分时间T,表示积分速度的快慢。当输入偏差信号△做阶跃变化时： (37) 式中：A一—阶跃变化的幅度。 32.3.3积分调节的特点 (1)能消除余差。积分调节与比例调节不同，其输出的调节信号和输入偏差之间没有 一对应的关系。只要有偏差存在，（即△≠0），输出调节信号就不断地变化，执行器就不 断他动作，直到扣信差信县消除 (2)调节动作缓慢。这时由于它的输出信号△u是由零开始积分的， 并随着时间逐渐积 累，在偏差△出现的瞬间，还是无调节作用，它的调节作用在时间上总是落后于偏差信 号的变化。 3.2.3.4积分调节的传递函数 积分调节器的传递函数可表示为： G(s)= U(S) E(s)Ts (39) 其方块图表示为图3-5 图一 图35积分调节器传递函数方块图

6 3.2.3 积分调节（I） 3.2.3.1 积分调节规律（I） 积分调节规律就是调节器的输出变化量与输入偏差随时间的积分成正比的调节规律， 亦即调节器输出的变化速度与输入偏差的大小成正比。所以只要有偏差，调节器输出的变 化速度就不等于零，当偏差为零时，输出就保持不变，而不管当时的阀位是多少。因此， 调节器有差即动，无差则停。可见，积分作用是能消除余差的。 积分调节规律可用下式表示： e T K e dt du I = I   =   1 (3-5) 或：    =   =   t I t I e dt T U K e dt 0 0 1 (3-6) 式中： KI——积分速度 TI——积分时间 3.2.3.2 积分时间 积分时间 TI 表示积分速度的快慢。当输入偏差信号△e 做阶跃变化时： A t T Adt T e dt T U I I t I  =   = =     1 1 1 0 （3-7） 式中：A——阶跃变化的幅度。 3.2.3.3 积分调节的特点 (1)能消除余差。积分调节与比例调节不同，其输出的调节信号和输入偏差之间没有一 一对应的关系。只要有偏差存在，（即△e ≠0），输出调节信号就不断地变化，执行器就不 断地动作，直到把偏差信号消除。 (2)调节动作缓慢。这时由于它的输出信号△u 是由零开始积分的，并随着时间逐渐积 累，在偏差△e 出现的瞬间，还是无调节作用，它的调节作用在时间上总是落后于偏差信 号的变化。 3.2.3.4 积分调节的传递函数 积分调节器的传递函数可表示为： E s T s U s G s I 1 ( ) ( ) ( ) = = （3-9） 其方块图表示为图 3-5 图 3-5 积分调节器传递函数方块图 （重点，该部 分是考点）

3.2.4微分调节(D) 3.24.1微分调节规律(D) 比例调节规律和积分调节规律都是根据被调参数与给定值的偏差动作的，而微分调节 想律则是根据信差的变化挡势（即变化速府）来动作的。这样我们可以在偏差的变化前面 采取措施，当发现偏差有迅速发展的可能时， 可施加 个较大的调节作用予以抑制，这样 就有可能减小偏差的变化幅度，改善调节品质，微分调节规律可以完成其功能。 微分调节作用与偏差变化速度的关系是： Au=T x dAe (3-10) (重点，该部 分是考点) 式中】 △一一微分调节器输出的变化量 d△edt 输入局差对时间的导数 TD一一微分时间 3.2.4.2微分调节作用的特点 微分调节作用是根据偏差的变化速度来调节的，所以它的输出快。有时尽管偏差很小 但只要它的变化速度很快 则微分调节就有 个较大的出去进行调节。它的作用比比积 调节作用(P)还要快，因此调节迅速。对于一些惯性很大（或容量滞后很大）的调节对象 可用它来改善调节质量。但是，当被调参数稳定在某一数值之后，微分作用就停止了，此 时，即使有很大偏差，调节器也不再动作。因此，纯微分作用还达不到消除偏差的目的。 3243微分调节的传递函数 微分调节器传递函数： Gu)-U-Ta (3-11 E(s) 微分调节器传递函数方块图如图37所示： 图3-7微分调节器传递函数方块图 3.2.5比例积分调节(P) 3.25.1特性 比例积分调节规律又称PI调节规律。它既具有比例调节动作，又具有积分调节动作 比例作用快，但不能消除偏差：积分作用稍慢于比例作用，但最终可以消除偏差。积分作 用就相当于在比例调节之后，再自动进行调整。故PI调节器又称为“再调调节器”，或称 “重定调节器”。P调节器的动作规律后可用下式表示： U=V,+U,=K,(Ne+ISe-di) (3-12) 式中：U -比例积分作用：U 一比例作用：U一 一积分作用 调节器的输出为比例作用和积分作用之和，而第二项多了一个比例系数K即，这是因为 在PI调节器的结构上，比例系数Kp不仅影响到比例部分，而且也影响到积分部分。这就 是说，这样使偏差随时间积累的速度加快了。 >

7 3.2.4 微分调节（D） 3.2.4.1 微分调节规律（D） 比例调节规律和积分调节规律都是根据被调参数与给定值的偏差动作的，而微分调节 规律则是根据偏差的变化趋势（即变化速度）来动作的。这样我们可以在偏差的变化前面 采取措施，当发现偏差有迅速发展的可能时，可施加一个较大的调节作用予以抑制，这样 就有可能减小偏差的变化幅度，改善调节品质，微分调节规律可以完成其功能。 微分调节作用与偏差变化速度的关系是： dt d e u TD   =  （3-10） 式中 ： Δu——微分调节器输出的变化量 dΔe/dt——输入偏差对时间的导数 TD——微分时间 3.2.4.2 微分调节作用的特点 微分调节作用是根据偏差的变化速度来调节的，所以它的输出快。有时尽管偏差很小， 但只要它的变化速度很快，则微分调节就有一个较大的输出去进行调节。它的作用比比例 调节作用（P）还要快，因此调节迅速。对于一些惯性很大（或容量滞后很大）的调节对象， 可用它来改善调节质量。但是，当被调参数稳定在某一数值之后，微分作用就停止了，此 时，即使有很大偏差，调节器也不再动作。因此，纯微分作用还达不到消除偏差的目的。 3.2.4.3 微分调节的传递函数 微分调节器传递函数： T s E s U s G s = = D ( ) ( ) ( ) （3-11） 微分调节器传递函数方块图如图 3-7 所示： 图 3-7 微分调节器传递函数方块图 3.2.5 比例积分调节（PI） 3.2.5.1 特性 比例积分调节规律又称 PI 调节规律。它既具有比例调节动作，又具有积分调节动作。 比例作用快，但不能消除偏差；积分作用稍慢于比例作用，但最终可以消除偏差。积分作 用就相当于在比例调节之后，再自动进行调整。故 PI 调节器又称为“再调调节器”，或称 “重定调节器”。PI 调节器的动作规律后可用下式表示： ) 1 (  = + =  + e  dt T U U U K e I P I P （3-12） 式中：U——比例积分作用；UP——比例作用；UI——积分作用 调节器的输出为比例作用和积分作用之和，而第二项多了一个比例系数 Kp，这是因为 在 PI 调节器的结构上，比例系数 Kp 不仅影响到比例部分，而且也影响到积分部分。这就 是说，这样使偏差随时间积累的速度加快了。 （重点，该部 分是考点）

3.2.5.2比例积分调节的特点 ()能消除静差。由于有积分作用，所以只要有偏差存在，调节器就能使输出朝若减小 偏差的方向，以一定的速度增加或减小。偏差越大，输出变化也越大。只有偏差为零时 输出才能稳定不变 (2)积分作用强弱，用积分时间T来衡量。积分时间T愈小，积分作用就愈强。组成 系统后，消除静差的速度也就越快，但也越容易产生振荡。 (3)系统若进入稳定状态，输出有可能不稳定，这时输出的变化仅仅取决于外界条件的 影响。 (4)存在积分饱和现象。具有积分作用的调节器，只要被调量与设定值之间有偏差其 输出就会不停的变化。如果由于某种原因（如阀门关闭、泵故障等），被调量偏差一时无 法消除，然而调节器这时还是要试图校正这个偏差，结果经过一段时间后，调节器输出 将进入深度饱和状态，这种现象称为积分饱和。进入深度积分饱和的调节器，要等被调 量信差反向以后才慢慢从饱和状态中退出来，面新恢复控制作用。 克服积分饱和可以采用如下两种方法 接入外部积分反馈、调节器内部实现 之间调节动作的自动切换。 3.2.5.3比例积分调节的传递函数 比例积分调节器的传递函数可表示为： K。△e1+ (3-14 E(s) Ae =K,0+3 若用比例度6来表示则为： c=0+ (3-15) 把传递函数画成方块图表示为图3-9 图39比例积分调节器传递函数方块图 3.2.6比例徽分调节(PD) 3.2.6.1特性 比例微分调节器的调节动作是比例调节与微分调节二者之和。 其数学表达式为： (3-16) 32.6.2比例微分调节的传递函数 比例微分调节器的传递函数为： 00-k0+7 (3-19)

8 3.2.5.2 比例积分调节的特点 (1)能消除静差。由于有积分作用，所以只要有偏差存在，调节器就能使输出朝着减小 偏差的方向，以一定的速度增加或减小。偏差越大，输出变化也越大。只有偏差为零时， 输出才能稳定不变。 (2)积分作用强弱，用积分时间 TI来衡量。积分时间 TI愈小，积分作用就愈强。组成 系统后，消除静差的速度也就越快，但也越容易产生振荡。 (3)系统若进入稳定状态，输出有可能不稳定，这时输出的变化仅仅取决于外界条件的 影响。 (4)存在积分饱和现象。具有积分作用的调节器，只要被调量与设定值之间有偏差,其 输出就会不停的变化。如果由于某种原因（如阀门关闭、泵故障等），被调量偏差一时无 法消除，然而调节器这时还是要试图校正这个偏差，结果经过一段时间后，调节器输出 将进入深度饱和状态，这种现象称为积分饱和。进入深度积分饱和的调节器，要等被调 量偏差反向以后才慢慢从饱和状态中退出来，重新恢复控制作用。 克服积分饱和可以采用如下两种方法：接入外部积分反馈、调节器内部实现 PI←→P 之间调节动作的自动切换。 3.2.5.3 比例积分调节的传递函数 比例积分调节器的传递函数可表示为： ) 1 (1 ) 1 (1 ( ) ( ) ( ) T s K e T S K e E s U s G s I P I P =  +    + = = （3-14） 若用比例度δ来表示则为： ) 1 (1 1 ( ) T s G s I = +  （3-15） 把传递函数画成方块图表示为图 3-9 图 3-9 比例积分调节器传递函数方块图 3.2.6 比例微分调节（PD） 3.2.6.1 特性 比例微分调节器的调节动作是比例调节与微分调节二者之和。 其数学表达式为： ( ) dt d e U UP UD KP e TD  = + =  +  (3-16) 3.2.6.2 比例微分调节的传递函数 比例微分调节器的传递函数为： (1 ) ( ) ( ) ( ) K T s E s U s G s = = P + D （3-19）

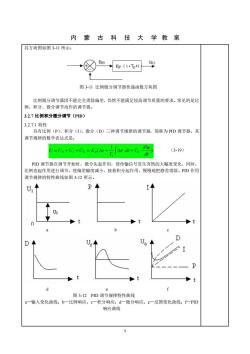
内蒙古科技大学教案 其方块图如图3-11所示： +☒酚即4 图31比例微分调节器传递函数方块图 比例微分调节器因不能完全消除偏差，仍然不能满足较高调节质量的要求。常见的是比 例、积分、微分调节动作的调节器。 3.2.7比例积分微分调节(PD) 3,2.71特性 具有比例(P)、积分(1)微分(D)三种调节规律的调节器，简称为D调节器。其 调节规律的数学表达式是： U=U,+U,+U=K,(e+7 dhe Ae-dt+To di (3-19) PD调节器在调节开始时，微分先起作用，使传输信号发生突然的大幅度变化，同时 比例也起作用进行调节，使偏差幅度减小，接着积分起作用，慢慢地把静差消除。PD作用 调节规律的特性曲线如图3-12所示。 图3-12PID调节规律特性曲线 一输入变化曲线：b一比例响应：。一积分响应：d一微分响应：。一反馈变化曲线：一PD 响应曲线

9 内 蒙 古 科 技 大 学 教 案 其方块图如图 3-11 所示： 图 3-11 比例微分调节器传递函数方块图 比例微分调节器因不能完全消除偏差，仍然不能满足较高调节质量的要求。常见的是比 例、积分、微分调节动作的调节器。 3.2.7 比例积分微分调节（PID） 3.2.7.1 特性 具有比例（P）、积分（I）、微分（D）三种调节规律的调节器，简称为 PID 调节器。其 调节规律的数学表达式是： ) 1 ( dt d e e dt T T U U U U K e D I P I D P  = + + =  +   +   （3-19） PID 调节器在调节开始时，微分先起作用，使传输信号发生突然的大幅度变化，同时， 比例也起作用进行调节，使偏差幅度减小，接着积分起作用，慢慢地把静差消除。PID 作用 调节规律的特性曲线如图 3-12 所示。 a b c d e f 图 3-12 PID 调节规律特性曲线 a—输入变化曲线；b—比例响应；c—积分响应；d—微分响应；e—反馈变化曲线；f—PID 响应曲线

内蒙古科技大学教案 3.2.7.2传递函数 比例积分微分调节器的传递函数为： G()-U=K(+T+ E(s) s (3-20 PD调节器的传递函数方块图如3-13所示。 输入 输出 测是元件 图3-13比例积分微分传递函数方块图 3.3PD调节规律对系统过渡过程的影响 3.3.1比例带对过渡过程的影响 比例作用能够较快地克服扰动对被调参数的影响，使系统稳定，它克服扰动的能力随 着偏差的增大而增大。因此比例作用是调节器的主要作 由于在比例调村 残差随 的力 而加大 因此从这一方面考虑，人们希望 尽量减小比例带。然而，减小比例带就等于加大了调节系统的开环增益k,其结果是号 致系统激烈振荡不稳定。稳定性是任何闭环控制的首要要求，比例带的设置必须保证系统 有一定的稳定裕度。 比例府8对被调参数的影的见图3.14所示 δ很大(K,减小)意味着调节阀的动作幅度很小，因此被调量的变化比较平稳，甚至 可以没有超调， 但残差很大，调节时间也很长（图3-14中曲线c、d、):当6再进一步 增大时，系统出现不振荡的过渡过程（曲线）。 减小6(K增大)就加大了调节阀的动作幅度，引起被调量来回波动，但系统仍可能 是稳定的。残差相应减小。 (考点) 8且有一个临界值 此时系统处于稳定边界的情况，进一步减小ǒ，系统就不稳定了 我们把这个临界值称为“临界比例度”，（曲线b:若用比例带表示则称“界匙例圈 。 当8<⑥：时，系统出现发散振荡的不稳定过程（曲线），这是不允许的。 从系统的稳定性要求出发，δ大一些（即K。小一些）为好，但从调节过程的准确性 要求来看，。小一些为好。可见，过程控制系统的准确性与稳定性之间存在着矛盾，通常 视具体要求，统筹考虑。 当比例度δ由大变小（即K,由小一大）时，它对调节过程中其它几个质量指标影响 见表31所示

10 内 蒙 古 科 技 大 学 教 案 3.2.7.2 传递函数 比例积分微分调节器的传递函数为： ) 1 (1 ( ) ( ) ( ) T s K T s E s U s G s I = = P + D + (3-20) PID 调节器的传递函数方块图如 3-13 所示。 图 3-13 比例积分微分传递函数方块图 3.3 PID 调节规律对系统过渡过程的影响 3.3.1 比例带对过渡过程的影响 比例作用能够较快地克服扰动对被调参数的影响，使系统稳定，它克服扰动的能力随 着偏差的增大而增大。因此比例作用是调节器的主要作用。 由于在比例调节中，残差随着比例带的加大而加大。因此从这一方面考虑，人们希望 尽量减小比例带。然而，减小比例带就等于加大了调节系统的开环增益 kp，其结果是导 致系统激烈振荡不稳定。稳定性是任何闭环控制的首要要求，比例带的设置必须保证系统 有一定的稳定裕度。 比例度 δ 对被调参数的影响见图 3-14 所示。 δ 很大（Kp 减小）意味着调节阀的动作幅度很小，因此被调量的变化比较平稳，甚至 可以没有超调，但残差很大，调节时间也很长（图 3-14 中曲线 c、d、e）；当 δ 再进一步 增大时，系统出现不振荡的过渡过程（曲线 f）。 减小 δ（Kp 增大）就加大了调节阀的动作幅度，引起被调量来回波动，但系统仍可能 是稳定的，残差相应减小。 δ 具有一个临界值，此时系统处于稳定边界的情况，进一步减小 δ，系统就不稳定了， 我们把这个临界值称为“临界比例度 δk”，（曲线 b）；若用比例带表示则称“临界比例带 P”。 当 δ<δk 时，系统出现发散振荡的不稳定过程（曲线 a),这是不允许的。 从系统的稳定性要求出发，δ 大一些（即 Kp 小一些）为好，但从调节过程的准确性 要求来看，δ 小一些为好。可见，过程控制系统的准确性与稳定性之间存在着矛盾，通常 视具体要求，统筹考虑。 当比例度 δ 由大变小（即 Kp 由小→大）时，它对调节过程中其它几个质量指标影响 见表 3-1 所示。 （考点）