北京邮电大学出版社：21世纪高等学校规划教材《高等数学》课程教学资源（PPT课件讲稿）第6章 空间解析几何 3平面及其方程

第3为 第六章 平面及其方程 平面的点法式方程 二、 平面的一般式方程 三、两个平面的夹角 四、平面外一点到平面的距离 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 第3节 一、平面的点法式方程 二、平面的一般式方程 三、两个平面的夹角 平面及其方程 第六章 四、平面外一点到平面的距离

一、平面的点法式方程 设一平面通过已知点M(xo,y,2o)且垂直于非零向 量=(A,B,C),求该平面I的方程 任取点M(x,y,)eⅡ，则有 MoM Ln 故 MoM.n=0 MoM=(x-x0y-0,2-0） A(x-xo)+By-yo)+C(2-0)=0 称①式为平面Π的点法式方程，称为平面Ⅱ的法向量 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 O  z y x M0 n ① 一、平面的点法式方程 ( , , ) 0 0 0 0 设一平面通过已知点 M x y z 且垂直于非零向 A(x − x0 ) + B(y − y0 ) +C(z − z0 ) = 0 M 称①式为平面的点法式方程, 求该平面的方程. 任取点M (x, y,z), 法向量. 量 n = (A , B, C), M0M ⊥n M0M n = 0 则有 故 称 n为平面 的

例6.3.2求过两点M1(1,0,-1),M2(-2,1,3),并且与向量 a=2-+平行的平面的方程 解：取法向量为 n=a×MM2={2,-1,1}×{-31,4} 2 -1 ={-5,-11,-1} -31 4 =-{5,11,1} 又M(1,0,-1),则所求平面的方程为 5(x-1)+11(y-0)+(z+1)=0, 即 5x+11y+z-4=0. BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 i j k = 例6.3.2 求过两点 (1,0, 1), 又M1 − = −{5,11,1}. 解: 取法向量为 a = 2i－j＋k平行的平面的方程. 则所求平面的方程为 2 −1 1 −3 1 4 n {2, 1,1} { 3,1,4} = aM1 M2 = −  − ={−5,−11,−1}

二、平面的一般式方程 设有三元一次方程 Ax+By+C=+D=0(42+B2+C2#0) ② 任取一组满足上述方程的数x0,y%,0,则 4xo+Byo+Czo+D=0 以上两式相减，得平面的点法式方程 A(x-xo)+B(y-y0)+C(2-2o)=0 显然方程②与此点法式方程等价，因此方程②的图形是 法向量为=(A,B,C)的平面，此方程称为平面的一般 式方程 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 二、平面的一般式方程 设有三元一次方程 以上两式相减 , 得平面的点法式方程 此方程称为平面的一般 Ax + By +Cz + D = 0 任取一组满足上述方程的数 , , , 0 0 0 x y z 则 Ax0 + B y0 +C z0 + D = 0 显然方程②与此点法式方程等价, ( 0) 2 2 2 A + B +C  ② n = (A,B,C) 的平面, 因此方程②的图形是 法向量为 式方程

Ax+By+Cz+D=0(42+B2+C20) 特殊情形 ·当D=0时，Ax+By+Cz=0表示通过原点的平面 ·当A=0时，By+Cz+D=0的法向量 n=(0,B,C)⊥i,平面平行于x轴： ·Ax+Cz+D=0表示平行于y轴的平面 ·Ax+By+D=0表示平行于z轴的平面； ·Cz+D=0表示平行于xOy面的平面， ·Ax+D=0表示平行于yOz面的平面； ·By+D=0表示平行于zOx面的平面 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 特殊情形 • 当 D = 0 时, A x + B y + C z = 0 表示通过原点的平面; • 当 A = 0 时, B y + C z + D = 0 的法向量 平面平行于 x 轴; • A x+C z+D = 0 表示 • A x+B y+D = 0 表示 • C z + D = 0 表示 • A x + D =0 表示 • B y + D = 0 表示 Ax + By +Cz + D = 0 ( 0) 2 2 2 A + B +C  平行于 y 轴的平面; 平行于 z 轴的平面; 平行于 xOy 面 的平面; 平行于 yOz 面 的平面； 平行于 zOx 面 的平面. n = (0,B,C) ⊥ i

例6.3.3求通过x轴和点(4，-3，-1)的平面方程 解：因平面通过x轴，故A=D=0 设所求平面方程为 By+Cz=0 代入已知点(4，-3，-1)得C=-3B 化简，得所求平面方程 y-3z=0 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 例6.3.3 求通过 x 轴和点( 4, – 3, – 1) 的平面方程. 解: 因平面通过 x 轴 , 故 A = D = 0 设所求平面方程为 By +Cz = 0 代入已知点 (4, −3, −1) 得 化简,得所求平面方程

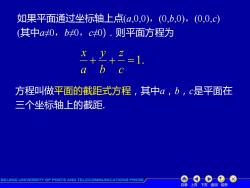
如果平面通过坐标轴上点(a,0,0),(0,b,0),(0,0,c) (其中a0,b0,c0).则平面方程为 x++2=1. b 方程叫做平面的截距式方程，其中α，b,c是平面在 三个坐标轴上的截距， BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 如果平面通过坐标轴上点(a,0,0)，(0,b,0)，(0,0,c) (其中a≠0，b≠0，c≠0)．则平面方程为 + + =1. c z b y a x 方程叫做平面的截距式方程，其中a，b，c是平面在 三个坐标轴上的截距

三、两个平面的夹角 两个平面法向量的夹角（常指锐角）称为平面的夹角 设平面的法向量为=(4，B1,C) 平面的法向量为2=(42，B2,C2) 则两平面夹角θ的余弦为 cosθ 即 A4 BiB2 CiC2 cos0 VA2+B2+C2V22+B22+C2 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 三、两个平面的夹角 设平面∏1的法向量为 平面∏2的法向量为 则两平面夹角 的余弦为 cos = 即 A1A2 + B1B2 +C1C2 2 2 2 2 2 A2 + B +C 2 1 2 1 2 A1 + B +C 两个平面法向量的夹角(常指锐角)称为平面的夹角. 1 2  n2 n1  ( , , ) n1 = A1 B1 C1 ( , , ) n2 = A2 B2 C2 1 2 1 2 cos n n n  n  =

Π1：万=(A,B1,C1) n1·2 Π2：n2=(42,B2,C2)） COs0= 特别有下列结论： ()卫1Π2=1 =A1A2+BB2+C1C2=0 (2)Π1/Π2，一元/元 A B, BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 2 特别有下列结论： 1 2 (1)  ⊥  A1 A2 + B1 B2 +C1C2 = 0 1 2 (2)  // 2 1 2 1 2 1 C C B B A A = = 1 1 2 1 2 1 2 cos n n n  n  = n1 ⊥ n2 1 2 n // n n2 n1 n2 n1 : ( , , ) : ( , , ) 2 2 2 2 2 1 1 1 1 1 n A B C n A B C  =  =

例6.3.6 求两平面2x-y+z-7=0和x+y+2z-11=0 的夹角 解：两平面的法向量分别为乃={2，-1,1}，2={1,1,2 12×1+(-1)×1+1×2 cos0 V22+(-1D2+12×√12+1+22 2 因此，夹角9=7 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 例6.3.6 求两平面2x－y + z －7 = 0和x +y +2z －11=0 的夹角. 解: 两平面的法向量分别为