北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第10章 无穷级数 2常数项级数的审敛法

第2节 第十章 常款项级款的审敛法 正项级数及其审敛法 二、交错级数及其审敛法 三、绝对收敛与条件收敛 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 二、交错级数及其审敛法 三、绝对收敛与条件收敛 第2节 一、正项级数及其审敛法 常数项级数的审敛法 第十章

一、正项级数及其审敛法 00 若4n≥0,则称∑4n 为正项级数 n=l 定理1正项级数∑4n收敛 二部分和数列{} n=l (n=1,2,…)有界 证:“→”若∑4n收敛,则{s}收敛故有界 n=1 一”un≥0,.部分和数列{sn}单调递增 又已知{s,}有界故{s,}收敛,从而∑4n也收敛 n=1 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 一、正项级数及其审敛法 若 0, un n=1 un 定理 1 正项级数 收敛 部分和数列 有界. 若 收敛 , ∴部分和数列 又已知 有界, 故 从而 故有界. 则称 为正项级数. 单调递增, 收敛 , 也收敛. 证: “ ” “ ” 则 收敛

定理2(比较审敛法) 设∑n∑n 都是正项级数, 且un≤Vn(n=1,2,…) (1)如果级数∑y,收敛,则级数∑4n也收敛: n=1 (2)如果级数 ∑4发散,则级数∑y,也发散 n=1 n=1 证:(1)由定理1可知,当级数∑y收敛时,其部分和 数列必有界,于是有心0,使得 0s∑y≤M BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 定理2 (比较审敛法) 设 且 (1) 如果级数 则级数 (2) 如果级数 则级数 收敛 , 也收敛 ; 发散 , 也发散. 都是正项级数, (n=1,2,…) . 证:(1)由定理1可知,当级数 收敛时,其部分和 数列必有界,于是有M>0,使得
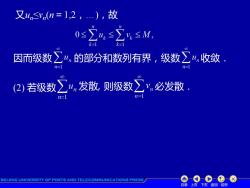
又4n≤n(n=1,2,…),故 0s∑4,≤∑≤M, 因而级数∑4的部分和数列有界,级数∑收敛. m=1 n=1 2)若级数∑4,发散则级数立y,必发散. =1 n=] BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 又un≤vn (n=1,2,…),故 因而级数 的部分和数列有界,级数 收敛. (2) 若级数 发散, 则级数 必发散.

准论设∑4∑ 都是正项级数,并且4n≤wm 0 (0,n2N,N为某一自然数). (1)如果级数 ∑收敛,则级数∑ 4n也收敛; n=1 n=1 (2)如果级数∑4,发散,则级数∑yn也发散. n=1 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 推论 设 (1) 如果级数 则级数 (2) 如果级数 则级数 收敛 , 也收敛 ; 发散 , 也发散 . 都是正项级数,并且un≤kvn ( k>0,n≥N,N为某一自然数 )
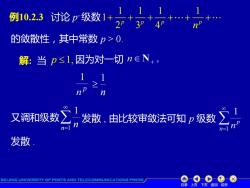
例10.2.3 讨论级数++…+ 的敛散性,其中常数p>0. 解:当p≤1,因为对一切n∈N+, n 又调和级数 发激,由比纹审敛法可知P级数。 n= 发散. BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 例10.2.3 讨论 p -级数 1 1 1 1 1 234 p p p p n + + + + + + 的敛散性,其中常数 p > 0. 解: 当 p 1, 因为对一切 又调和级数 =1 1 n n 由比较审敛法可知 p 级数 n 1 发散 . 发散

当p>1,因为当n-1≤x≤n时 , 故 dx [-][ 故级数收敛,由比较审敛法知p级数收敛 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 p 1, 因为当 , 1 1 p p n x 故 − = n n p p x n 1 n d 1 1 − n n p x 1 x d 1 − − − = −1 −1 1 ( 1) 1 1 1 p p p n n 考虑强级数 − − − − = 1 1 2 1 ( 1) 1 p p n n n 的部分和 n + − = − − = 1 1 1 ( 1) 1 1 p p n k k k n → 故级数收敛 , 由比较审敛法知 p 级数收敛 . 时, 1 ( 1) 1 1 − + = − p n 1 当 + + + − + − − −1 −1 −1 −1 −1 ( 1) 1 1 3 1 2 1 2 1 1 p p p p p n n

例10.2.4判定级数 的敛散性 解:因为 3= √n(n+in+ly (n=1,2,…) 而级数 发散 k=2 根据比较审敛法可知,所给级数发散 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 判定级数 的敛散性. 解: 因为 2 ( 1) 1 ( 1) 1 + n n + n 而级数 = = 2 1 k k 发散 根据比较审敛法可知, 所给级数发散 . 例10.2.4

定理3(比较审敛法的极限形式) 设两正项级数 00 ∑4n,∑Yn满足lim4n=1,则有 n=1 7n=1 n→oVn (1)当0≤1N时, 42<1+1,即un<(0+y BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 定理3 (比较审敛法的极限形式) lim l, v u n n n = → 则有 (2) 当 l = +∞ 证: (1)由极限定义,对 设两正项级数 满足 (1) 当 0 ≤ l < +∞

00 而级数Σ'收敛,根据比较审敛法的推论,知级数 n=1 ∑4,收敛 n= (2)按已知条件 im”存在,如果级数∑u,收敛,则 n->Un n=1 由结论(1)必有∑yn收敛,但已知级数∑yn发散, 因此级数∑u,不可能收敛,即级数∑4n发散· n= BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束
目录 上页 下页 返回 结束 而级数 收敛,根据比较审敛法的推论,知级数 收敛. (2)按已知条件 存在,如果级数 收敛,则 由结论(1)必有 收敛,但已知级数 发散, 因此级数 不可能收敛,即级数 发散.
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第10章 无穷级数 1常数项级数的概念和性质.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第6章 空间解析几何 6空间曲线及其方程.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第6章 空间解析几何 5曲面及其方程.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第6章 空间解析几何 4空间直线及其方程.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第6章 空间解析几何 3平面及其方程.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第6章 空间解析几何 2向量的向量积.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第6章 空间解析几何 1预备知识.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第5章 定积分 7定积分的物理应用.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第5章 定积分 6定积分在几何学上的应用.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第5章 定积分 5广义积分.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第5章 定积分 4定积分的换元积分法和分部积分法.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第5章 定积分 3微积分基本公式.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第5章 定积分 2定积分的基本性质.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第5章 定积分 1定积分的概念.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第4章 不定积分 5有理函数和可化为有理函数的积分.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第4章 不定积分 4分部积分法.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第4章 不定积分 3第二类换元积分法.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第4章 不定积分 2第一类换元积分法.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第4章 不定积分 1不定积分的概念与性质.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第3章 微分中值定理与导数的应用 6弧微分与曲率.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第10章 无穷级数 3幂级数.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第10章 无穷级数 4函数展开成幂级数.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第10章 无穷级数 5傅里叶级数.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第7章 多元函数微分及其应用 1多元函数的基本概念与极限.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第7章 多元函数微分及其应用 2偏导数.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第7章 多元函数微分及其应用 3全微分及其应用.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第7章 多元函数微分及其应用 4复合函数与隐函数求导法.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第7章 多元函数微分及其应用 5方向导数与梯度.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第7章 多元函数微分及其应用 6微分法在几何上的应用.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第7章 多元函数微分及其应用 7多元函数的极值及其求法.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第8章 重积分 1二重积分的概念与性质.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第8章 重积分 2二重积分的计算.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第8章 重积分 3二重积分的应用.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第8章 重积分 4三重积分的概念及计算.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第9章 曲线积分与曲面积分 1对弧长的曲线积分.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第9章 曲线积分与曲面积分 2对坐标的曲线积分.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第9章 曲线积分与曲面积分 3格林公式及其应用.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第9章 曲线积分与曲面积分 4对面积的曲面积分.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第9章 曲线积分与曲面积分 5对坐标的曲面积分.ppt
- 北京邮电大学出版社:21世纪高等学校规划教材《高等数学》课程教学资源(PPT课件讲稿)第9章 曲线积分与曲面积分 6高斯公式与斯托克斯公式.ppt
