北京邮电大学出版社：21世纪高等学校规划教材《高等数学》课程教学资源（PPT课件讲稿）第10章 无穷级数 4函数展开成幂级数

第4为 第十章 岛数展开成暴级数 泰勒级数 二、 函数展开成幂级数 三、函数的幂级数展开式的应用 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 第4节 一、泰勒级数 二、函数展开成幂级数 函数展开成幂级数 第十章 三、函数的幂级数展开式的应用

一、泰勒级数 复习：f(x)的n阶泰勒公式 若函数f(x)在xo的某邻域内具有n+1阶导数，则在 该邻域内有 f(x)=f(%o)+f(%o)x-xo)+I"o(x-xo) 2川 ++fm（g-y+R, n! 其中Rn(x) f”(-(5在x与之间 (n+1)川 称为拉格朗日余项 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 一、泰勒级数 其中 Rn (x) = (  在 x 与 x0 之间) 称为拉格朗日余项. 1 0 ( 1) ( ) ( 1)! ( ) + + − + n n x x n f  则在 复习: f (x) 的 n 阶泰勒公式 f (x) = f (x0 ) + f (x0 )(x − x0 ) + 2 0 0 ( ) 2! ( ) x x f x −  n n x x n f x ( ) ! ( ) 0 0 ( ) ++ − R (x) + n 若函数 的某邻域内具有 n + 1 阶导数, 该邻域内有 :

若函数f(x)在x的某邻域内具有任意阶导数，则称 f)+FGox-x)+2(x-,月 21 ((x)"+ nl 为f(x)的泰勒级数 当x,=0时，泰勒级数又称为麦克劳林级数 待解决的问题 1)对此级数，它的收敛域是什么？ 2)在收敛域上，和函数是否为f(x)? BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 f (x0 ) + f (x0 )(x − x0 ) + 2 0 0 ( ) 2! ( ) x x f x −  ++ − n + n x x n f x ( ) ! ( ) 0 0 ( ) 为f (x) 的泰勒级数 . 则称 当x0 = 0 时, 泰勒级数又称为麦克劳林级数. 1) 对此级数, 它的收敛域是什么 ？ 2) 在收敛域上 , 和函数是否为 f (x) ? 待解决的问题 : 若函数 的某邻域内具有任意阶导数

定理1 设函数f(x)在点x的某一邻域U(xo)内具有 各阶导数，则f(x)在该邻域内能展开成泰勒级数的充要 条件是f(x)的泰勒公式余项满足：1imR,(x)=0. n->oo 证九-三/：-x八、a k=0 f(x)=S(x)+R,(x) lim R,(x)lim [f(x)-S,+(x)]=0,xEU(xo) n-→o0 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 定理1 各阶导数, 则 f (x) 在该邻域内能展开成泰勒级数的充要 条件是 f (x) 的泰勒公式余项满足: lim ( ) = 0. → R x n n 证明: ( ) , ! ( ) ( ) 0 0 0 ( ) n n n x x n f x f x =  −  = 令 ( ) ( ) ( ) 1 f x S x R x = n+ + n = → lim R (x) n n lim ( ) ( ) 1 f x S x n n + → − = 0 , ( ) 0 xU x k n k k n x x k f x S x ( ) ! ( ) ( ) 0 0 0 ( ) 1 =  − = + ( ) 0 xU x 设函数 f (x) 在点 x0 的某一邻域 内具有

定理2如果f(x)能展开成x的幂级数，则这种展开式是 唯一的，且与它的麦克劳林级数相同 证：设f(x)所展开成的幂级数为 f(x)=ao+ax+a2x2+…+anx”+…,x∈(-，R) 则 a=f(0) f'(x)=4+2a2x++nanx+;a,=f(0) f"(x)=21a2++nn-1)anx-2+…;a2=f"(0) f((x)=nlan+.. an =mf((0) 显然结论成立 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 定理2 如果f (x) 能展开成 x 的幂级数, 唯一的 , 且与它的麦克劳林级数相同. 证: 设 f (x) 所展开成的幂级数为 则 ( ) 2 ; 1 f  x = a1 + a2 x ++ nan x n− + (0) 1 a = f  ( ) 2! ( 1) ; 2 f  x = a2 ++ n n − an x n− + (0) 2! 1 2 a = f  ( ) ! ; f (n) x = n an + (0) ( ) ! 1 n n n a = f 显然结论成立 . (0) 0 a = f 则这种展开式是

二、 函数展开成幂级数 直接展开法一利用泰勒公式 展开方法 间接展开法一利用已知其级数展开式 1.直接展开法 的函数展开 由泰勒级数理论可知，函数f(x)展开成幂级数的步 骤如下 第一步求出x)的各阶导数， 第二步 求函数及其各阶导数在x=0处的值 第三步写出幂级数，并求出收敛半径R 第四步 判别在收敛区间(-R,R)内limR,(x)是否为 n>o∞ BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 二、函数展开成幂级数 1. 直接展开法 由泰勒级数理论可知, 函数 f (x)展开成幂级数的步 第一步 求出f(x)的各阶导数 ; 第二步 求函数及其各阶导数在x＝0处的值 ; 第四步 判别在收敛区间(－R, R) 内 lim R (x) n n→ 是否为 骤如下 : 展开方法 直接展开法 — 利用泰勒公式 间接展开法 — 利用已知其级数展开式 0. 的函数展开 第三步 写出幂级数，并求出收敛半径R

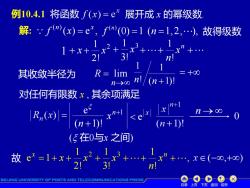
例10.4.1将函数f(x)=ex展开成x的幂级数 解：fm(x)=e,f(0)=1(n=1,2,2 故得级数 1+x+ 2 21 n 其收敛半径为 R=lim =十00 n-→o0 (n+1)月 对任何有限数x,其余项满足 n+l R,(x)= oo (n+1) (5在0与x之间) 故心=1+x+产+ 21 x”+…,x∈(-0，+0) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 例10.4.1 将函数 展开成 x 的幂级数. 解: ( ) e , (n) x  f x = ( ) (0) 1 ( 1,2, ), n f n = = 1 其收敛半径为 对任何有限数 x , 其余项满足  e (n +1)! n+1 x x  e 故 , ! 1 3! 1 2! 1 e 1 x = + + 2 + 3 ++ x n + n x x x → = n R lim ! 1 n ( 1)! 1 n + n → ( 在0与x 之间) + x 2 2! 1 + x 3 3! 1 + x ++ x n + n! 1 故得级数

例10.4.2将函数f(x)=sinx展开成x的幂级数 解：fm(x)=sin(x+n·5〉 o- n=2k (k=0,1,2,…） n=2k+1 得级数X-x3x5-+(-1”x21+… 其收敛半径为R=+∞，对任何有限数x,其余项满足 sin(5+(n+1)) n+1 IR () n0 (n+1)! (n+1)！ snx=x-京x+京x3-+(-1)” 十 x∈(-0，+00) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 例10.4.2 将函数 展开成 x 的幂级数. 解: ( ) = ( ) f x n      (0) = (n) f 得级数: x 其收敛半径为 R = +, 对任何有限数 x , 其余项满足 sin( ( 1) ) 2 π  + n + (n +1)! n+1 x n = 2k +1 (k = 0,1, 2, ) 3 3! 1 − x + −+ 5 5! 1 x 1 2 1 (2 1)! ( 1) + + n n n − + x  sin x n → n = 2k ( 1) , k − 0 , 2 1 1 1 3 5 3! 5! (2 1)! ( 1) + + n n x n = − + − + − + x x x

2.间接展开法 利用一些已知的函数展开式及幂级数的运算性质 将所给函数展开成幂级数 例10.4.4将函数 1+x2 展开成x的幂级数 解：因为 1=1+x+X2++x”+…(-1<x<1) 1- 把x换成-x2,得 1+x2=1-x+x-+(-1x2+… (-1<x<1) BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页返回结束

目录 上页 下页 返回 结束 2. 间接展开法 1 1 x = − 利用一些已知的函数展开式及幂级数的运算性质, 例10.4.4 将函数 展开成 x 的幂级数. 解: 因为 2 1 n + + + + + x x x (−1 x 1) 把 x 换成 2 −x = + 2 1 1 x 2 4 2 1 ( 1)n n − + − + − + x x x (−1 x 1) , 得 将所给函数展开成幂级数

例10.4.5将函数f(x)=1n1+x)展开成x的幂级数 解：f'(x)=, = ∑(-1)”x”(-1<x<1) 1+x n=0 从0到x积分，得 含yfra -1<x≤1 n=0 上式右端的幂级数在x=1收敛，而ln(1+x)在x=1有 定义且连续，所以展开式对x=1也是成立的，于是收敛 域为-1<x≤1. 利用此题可得 111 1n2=1- n+] BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS O< 目录上页下页返回结束

目录 上页 下页 返回 结束 例10.4.5 将函数 展开成 x 的幂级数. 解: x f x +  = 1 1 ( ) ( 1) ( 1 1) 0 =  − −    = x x n n n 从 0 到 x 积分, 得 x x x x n n n ln(1 ) ( 1) d 0 0    = + = − , 1 ( 1) 0 1   = + + − = n n n x n 定义且连续, 域为 利用此题可得 −−11xx11 上式右端的幂级数在 x ＝1 收敛 , 而 ln(1+ x)在x =1有 所以展开式对 x ＝1 也是成立的, 于是收敛