西安电子科技大学：《智能控制导论》课程教学课件（博弈控制）第一讲 博弈论简介

历些毛子代技大学 XIDIAN UNIVERSITY 博弈论简介 引子 ,20世纪著名的诺贝尔经济学奖得主莎缪尔 (Paul A.Samuelson,1915-2009) 曾经说过： 要想在现代社会做一个有文化的人， 必须对博弈论有一个大致的了解。 ,萨缪尔森于1970年（55岁)获得诺贝尔 经济学奖，是第一个获得诺贝尔经济学奖 的美国人

引子  20 世纪著名的诺贝尔经济学奖得主莎缪尔 森（Paul A. Samuelson，1915-2009） 曾经说过： 要想在现代社会做一个有文化的人， 必须对博弈论有一个大致的了解。  萨缪尔森于1970年（ 55岁）获得诺贝尔 经济学奖，是第一个获得诺贝尔经济学奖 的美国人。 博弈论简介

博弈论简介 引子 20世纪著名的诺贝尔经济学奖得主莎缪尔 (Paul A.Samuelson,1915-2009) 曾经说过： 要想在现代社会做一个有文化的人， 必须对博弈论有一个大致的了解。 ~萨缪尔森于1970年（55岁)获得诺贝尔 经济学奖，是第一个获得诺贝尔经济学奖 的美国人

引子  20 世纪著名的诺贝尔经济学奖得主莎缪尔 森（Paul A. Samuelson，1915-2009） 曾经说过： 要想在现代社会做一个有文化的人， 必须对博弈论有一个大致的了解。  萨缪尔森于1970年（ 55岁）获得诺贝尔 经济学奖，是第一个获得诺贝尔经济学奖 的美国人。 博弈论简介

博弈论简介 1、什么是博弈论 一个经典的例子：囚徒困境 ,两个共谋犯罪的人被关入监狱，不能互相沟通情况。如果 两个人都不揭发对方，则由于证据不确定，每个人都坐牢 一年；若一人揭发，而另一人沉默，则揭发者因为立功而 立即获释，沉默者因不合作而入狱十年；若互相揭发，则 因证据确实，二者都判刑五年。 ,由于囚徒无法信任对方，因此倾向于互相揭发，而不是同 守沉默。最终导致纳什均衡仅落在非合作点上

博弈论简介 1、什么是博弈论 一个经典的例子：囚徒困境  两个共谋犯罪的人被关入监狱，不能互相沟通情况。如果 两个人都不揭发对方，则由于证据不确定，每个人都坐牢 一年；若一人揭发，而另一人沉默，则揭发者因为立功而 立即获释，沉默者因不合作而入狱十年；若互相揭发，则 因证据确实，二者都判刑五年。  由于囚徒无法信任对方，因此倾向于互相揭发，而不是同 守沉默。最终导致纳什均衡仅落在非合作点上

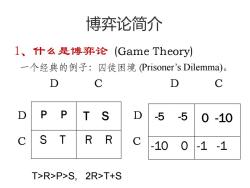
博弈论简介 1、什么是博弈论(Game Theory) 一个经典的例子：囚徒困境Prisoner's Dilemma)。 D C D C P T S D -5-5 0-10 T IR R C -100 -1-1 T>R>P>S,2R>T+S

博弈论简介 1、什么是博弈论 (Game Theory) 一个经典的例子：囚徒困境 (Prisoner’s Dilemma)。 D C D C D D C C -5 -5 0 -10 -10 0 -1 -1 P P T S S T R R T>R>P>S, 2R>T+S

博弈论简介 2、囚徒困境的启示 。(D,D)这个状态，谁也不能通过单方面改变自 己的策略增加自己的收益。因此，谁也不会主 动离开这个状态，即改变自己的策略为C。 。当然，这两个人可以订立攻守同盟，即合作， 这时的博弈状态是(C,C)

博弈论简介 2、囚徒困境的启示  (D, D)这个状态，谁也不能通过单方面改变自 己的策略增加自己的收益。因此，谁也不会主 动离开这个状态，即改变自己的策略为C。  当然，这两个人可以订立攻守同盟，即合作， 这时的博弈状态是(C, C)

博弈论简介 2、囚徒困境的启示（续） ·(C,C)这个状态是不稳定的，任何人都能 通过单方面改变自己的策略增加自己的 收益。因此，每个人都有意愿离开这个 状态，即改变自己的策略为D。 。囚徒困境反映了个人理性与集体利益的 矛盾

博弈论简介 2、囚徒困境的启示（续）  (C, C)这个状态是不稳定的，任何人都能 通过单方面改变自己的策略增加自己的 收益。因此，每个人都有意愿离开这个 状态，即改变自己的策略为D。  囚徒困境反映了个人理性与集体利益的 矛盾

3、纳什均衡 假设有n个玩家(agent,player)参与 博弈，给定其他人策略的条件下，每个玩 家选择自己的最优策略（个人最优策略可 能依赖于也可能不依赖于他人的策略)， 从而使自己效用最大化。所有局中人策略 构成一个策略组合(Strategy Profile)。 各个参与人的在某个时间点的策略的 有序集称为策略组合，比如囚徒困境中的 (D,D),(C,C),(C,D)都是策略组合

3、纳什均衡 假设有n个玩家(agent, player)参与 博弈，给定其他人策略的条件下，每个玩 家选择自己的最优策略（个人最优策略可 能依赖于也可能不依赖于他人的策略）， 从而使自己效用最大化。所有局中人策略 构成一个策略组合（Strategy Profile）。 各个参与人的在某个时间点的策略的 有序集称为策略组合，比如囚徒困境中的 (D, D), (C, C), (C, D)都是策略组合

3、纳什均衡 纳什均衡指的是这样一种策略组合，即在给 定别人策略的情况下，没有人愿意单方面改变自 己的策略，从而打破这种均衡

3、纳什均衡 纳什均衡指的是这样一种策略组合，即在给 定别人策略的情况下，没有人愿意单方面改变自 己的策略，从而打破这种均衡

4、纳什均的数学表示 博弈的数学表示： G={S1,…,Sn:u1,…,un} 其中，S表示参与人i的策略集合，也叫策略空间 比如：S={C,D},i=1,n。 u:是给定各个参与人的策略的情况下，参与人 的收益的计算函数，也叫收益函数 u(s1,…,sn)=f(s1,…,sn) 其中s;是参与人i所采用的策略

4、纳什均衡的数学表示 博弈的数学表示： G=﹛S1 ,…,Sn：u1 ,…,un﹜ 其中， Si表示参与人i的策略集合, 也叫策略空间。 比如： Si= {C, D}, i=1,…n。 ui是给定各个参与人的策略的情况下，参与人 i的收益的计算函数，也叫收益函数 ui（s1,…,sn）=f （s1,…,sn）， 其中si 是参与人i所采用的策略

4、纳什均的数学表示 纳什均衡的定义：在博弈 G={S1,…,Sn:u1,,un} 中，如果由各个博弈方的各一个策略组成的某个策 论组合(S,*,…,Sn*)中，任一博弈方的策略s都是 对其余博弈方策略的组合(S1*,S-1*,S+1*,…,Sn*) 的最佳对策，即 u(S1*,…S*,,Sn*）≥u(S1*,…,S,…,Sn*) 对任意s,∈S都成立，则称(s1*,…,s*,,Sn*)为 G的一个纳什均衡

4、纳什均衡的数学表示 纳什均衡的定义：在博弈 G=﹛S1 ,…,Sn：u1 ,…,un﹜ 中，如果由各个博弈方的各一个策略组成的某个策 论组合（s1*,…,sn *）中，任一博弈方i的策略si都是 对其余博弈方策略的组合（s1*,…si-1*,si+1*,…,sn *） 的最佳对策, 即 ui（s1*,…,si*, …, sn* ）≥ui（s1*,…, si , …, sn* ） 对任意si∈Si都成立，则称（s1*,…, si* , …, sn *）为 G的一个纳什均衡