西安电子科技大学：《智能控制导论》课程教学课件（博弈控制）第四讲 博弈的基本分析方法（上）

基本分析思路和方法 1上策均衡 2严格下策反复消去法 3划线法 4箭头法

基本分析思路和方法 1 上策均衡 2 严格下策反复消去法 3 划线法 4 箭头法

1上策均衡 上策：不管其它博弈方选择什么策略，一博弈方的 某个策略给他带来的得益始终高于他的其它的策 略，至少不低于其他策略的策略。 4,(s,S)≥4（⑤，5），对任意的3∈S,s≠， 智猪博弈中的小猪“等待”；囚徒的困境中的 “坦白”；双寡头削价中“低价”。 小猪 按 等 待 D 5-5 按 5,1 4,4 0-10 猪 等待 9，-1 0,0 -10 -1-1

1 上策均衡 上策：不管其它博弈方选择什么策略，一博弈方的 某个策略给他带来的得益始终高于他的其它的策 略，至少不低于其他策略的策略。 对任意的 智猪博弈中的小猪“等待”；囚徒的困境中的 “坦白”；双寡头削价中“低价”。 5， 1 4， 4 9， -1 0， 0 大 猪 按 等 待 小猪 按 等 待 -5 -5 0 -10 -10 0 -1 -1 D D C C ' ( , ) ( , ), i i i i i i u s s u s s    ' , i i s S  ' , i i s s 

1上策均衡 上策均衡：一个博弈的某个策略组合中的所有策略 都是各个博弈方各自的上策，必然是该博弈比较 稳定的结果 *上策均衡不是普遍存在的 *上策均衡肯定是纳什均衡，但纳什均衡不一定是 上策均衡 小猪 按 等待 5,1 4, 4 D -5-5 0-10 大 按 等待 9,-1 0, 0 -100-1-1

1 上策均衡 上策均衡：一个博弈的某个策略组合中的所有策略 都是各个博弈方各自的上策，必然是该博弈比较 稳定的结果  上策均衡不是普遍存在的  上策均衡肯定是纳什均衡，但纳什均衡不一定是 上策均衡 5， 1 4， 4 9， -1 0， 0 大 猪 按 等待 小猪 按 等 待 -5 -5 0 -10 -10 0 -1 -1 D D C C

2、严格下策反复消去法 严格下策：不管其它博弈方采用哪一个策略， 某一给一个博弈方带来的收益总是比另一种 策略给他带来的收益小的策略。 4,(s5)<4(S,5,对任意的s,seS,≠s, 严格下策反复消去： 左 中 右 左 中 左 中 上 1,0 1,3 0,1 1,0 1,3 1,0 1,3 下 0,4 0,2 2,0 0,4 0,2

2 、严格下策反复消去法 严格下策：不管其它博弈方采用哪一个策略， 某一给一个博弈方带来的收益总是比另一种 策略给他带来的收益小的策略。 对任意的 ， 严格下策反复消去： 1，0 1，3 0，1 0，4 0，2 2，0 左 中 右 上 下 1，0 1，3 0，4 0，2 左 中 1，0 1，3 左 中 ' ( , ) ( , ), i i i i i i u s s u s s    ' , i i s S  ' , i i si s s 

纳什均衡与严格下策反复消去法 命题1：在n个博弈方的博弈G={S1,…Sn4,un}中，如果严格下 策反复消去法排除了除(S,…Sn之外的所有策略组合，那么 (s1,…s) 一定是该博奔的唯一的纳什均衡 命题2：在n个博弈方的博弈中G={S,…Sm4,…un}中，如果 (s,s,)是G的一个纳什均衡，那么严格下策反复消去法一定 不会将它消去 上述两个命题保证在进行纳什均衡分析之前先通过严格下策 反复消去法简化博弈是可行的

纳什均衡与严格下策反复消去法 命题1：在n个博弈方的博弈 中，如果严格下 策反复消去法排除了除 之外的所有策略组合，那么 一定是该博弈的唯一的纳什均衡 命题2：在n个博弈方的博弈中 中，如果 是 的一个纳什均衡，那么严格下策反复消去法一定 不会将它消去 上述两个命题保证在进行纳什均衡分析之前先通过严格下策 反复消去法简化博弈是可行的 ( , ) * * i n s s { , ; , } G  S1 Sn u1 un ( , ) * * i n s s ( , ) * * i n s s { , ; , } G  S1 Sn u1 un G

纳什均衡与严格下策反复消去法 弱下策：不管其它博弈方采用哪一个策略，某一策略给一个博 弈方带来的收益总是比另一种策略给他带来的收益小，至多 相等的策略。 4(s,s)≤4(s,S),对任意的5，SeS，≠S 弱下策能不能消去：俾斯麦海战 1943年，日本海军上将木村受命将日本陆军运抵新几内亚，期间 要穿越俾斯麦海。而美国海军上将肯尼欲对日本船队进行轰 炸。穿越俾斯麦海到新几内亚有两条线路：较短的北线和较 长的南线。木村必须选择一条线路，而肯尼也必须选择一条

纳什均衡与严格下策反复消去法 弱下策：不管其它博弈方采用哪一个策略，某一策略给一个博 弈方带来的收益总是比另一种策略给他带来的收益小，至多 相等的策略。 对任意的 ， 弱下策能不能消去：俾斯麦海战 1943年，日本海军上将木村受命将日本陆军运抵新几内亚，期间 要穿越俾斯麦海。而美国海军上将肯尼欲对日本船队进行轰 炸。穿越俾斯麦海到新几内亚有两条线路：较短的北线和较 长的南线。木村必须选择一条线路，而肯尼也必须选择一条 ' ( , ) ( , ), i i i i i i u s s u s s    ' , i i s S  ' , i i si s s 

纳什均衡与严格下策反复消去法 弱下策能不能消去：俾斯麦海战（续） 线路去搜索日军。如果肯尼将飞机派往错误的线路，召回需 要时间，轰炸时间会少几天。 对木村来说，南线是弱下策。对肯尼来说，他知道南线是木 村的弱下策，因此他也选择北线，当年就是 木村 北线 南线 这么发生的。 肯北线 2,-2 2,-2 但是，如果木村知道肯尼要选择北线，尼南线 1,-1 3,3 他也可能选南线，（北线，南线)也可能为最后结果

纳什均衡与严格下策反复消去法 弱下策能不能消去：俾斯麦海战（续） 线路去搜索日军。如果肯尼将飞机派往错误的线路，召回需 要时间，轰炸时间会少几天。 对木村来说，南线是弱下策。对肯尼来说，他知道南线是木 村的弱下策，因此他也选择北线，当年就是 这么发生的。 但是，如果木村知道肯尼要选择北线， 他也可能选南线，（北线，南线）也可能为最后结果。 2，-2 2，-2 1，-1 3，-3 北线 南线 北线 南线 木村 肯 尼

3划线法 * 给定其它参与人的策略，对当事参与人的各种策 略进行比较，在最好的策略下划线。最后，所有 策略均划线的策略组合是纳什均衡。 *例子 左 中 右 上 1,0 1,3 0,1 下 0,4 0,2 2,0 1, 0 1,3 0,1 0,4 0,2 2,0

3 划线法  给定其它参与人的策略，对当事参与人的各种策 略进行比较，在最好的策略下划线。最后，所有 策略均划线的策略组合是纳什均衡。  例子 1， 0 1， 3 0， 1 0， 4 0， 2 2， 0 左 中 右 上 下 1， 0 1， 3 0， 1 0， 4 0， 2 2， 0

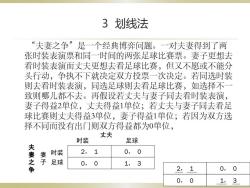
3划线法 “夫妻之争”是一个经典博弈问题。一对夫妻得到了两 张时装表演票和同一时间的两张足球比赛票。妻子更想去 看时装表演而丈夫更想去看足球比赛，但又不愿或不能分 头行动，争执不下就决定双方投票一次决定。若同选时装 则去看时装表演，同选足球则去看足球比赛，如选择不一 致则哪儿都不去。再假设若丈夫与妻子同去看时装表演， 妻子得益2单位，丈夫得益1单位，若丈夫与妻子同去看足 球比赛则丈夫得益3单位，妻子得益1单位；若因为双方选 择不同而没有出门则双方得益都为0单位， 丈夫 时装 足球 妻之 时装 2,1 0,0 子 足球 0,0 1,3 2,1 0,0 0,0 1,3

3 划线法 “夫妻之争”是一个经典博弈问题。一对夫妻得到了两 张时装表演票和同一时间的两张足球比赛票。妻子更想去 看时装表演而丈夫更想去看足球比赛，但又不愿或不能分 头行动，争执不下就决定双方投票一次决定。若同选时装 则去看时装表演，同选足球则去看足球比赛，如选择不一 致则哪儿都不去。再假设若丈夫与妻子同去看时装表演， 妻子得益2单位，丈夫得益1单位；若丈夫与妻子同去看足 球比赛则丈夫得益3单位，妻子得益1单位；若因为双方选 择不同而没有出门则双方得益都为0单位， 2， 1 0， 0 0， 0 1， 3 夫 妻 之 争 时装 足球 时装 足球 丈夫 妻 子 2， 1 0， 0 0， 0 1， 3

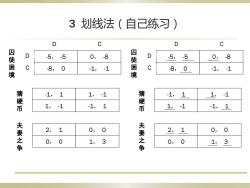
3划线法（自己练习） D C D C 四徒 D -5,-5 0,-8 D 5,-5 0,-8 境 C -8,0 -1,-1 四徒困境 -8,0 -1,-1 -1,1 1,-1 -1,1 1,-1 硬币 1,-1 -1,1 猜硬币 1,-1 -1,1 夫妻之争 2,1 0,0 2,1 0,0 0,0 1,3 夫妻之争 0,0 1,3

3 划线法（自己练习） -1， 1 1， -1 1， -1 -1， 1 猜 硬 币 2， 1 0， 0 0， 0 1， 3 夫 妻 之 争 -5， -5 0， -8 -8， 0 -1， -1 囚 徒 困 境 D C D C -1， 1 1， -1 1， -1 -1， 1 猜 硬 币 2， 1 0， 0 0， 0 1， 3 夫 妻 之 争 -5， -5 0， -8 -8， 0 -1， -1 囚 徒 困 境 D C D C