吉林大学：《自动控制原理》课程电子教案（PPT课件）第三章 控制系统的时域分析法 第四节 线性系统的稳态误差分析计算

第四节线性系统的稳态误差分析计算 控制系统的稳态误差，是控制精度（准确度） 的一种度量，是控制系统的稳态性能指标。在实 际系统中，引起稳态误差的因素是多种多样的。 本节仅仅讨论线性系统由于系统结构、参数 及输入信号形式不同所引起的稳态误差。 一，系统误差及稳态误差的概念 实际物理系统从其主反馈通道来看分为单位 反馈和非单位反馈两种基本结构形式如图3.27(a) 及(b)所示

第四节 线性系统的稳态误差分析计算 控制系统的稳态误差，是控制精度(准确度) 的一种度量，是控制系统的稳态性能指标。在实 际系统中，引起稳态误差的因素是多种多样的。 本节仅仅讨论线性系统由于系统结构、参数 及输入信号形式不同所引起的稳态误差。 一. 系统误差及稳态误差的概念 实际物理系统从其主反馈通道来看分为单位 反馈和非单位反馈两种基本结构形式如图3.27(a) 及(b)所示

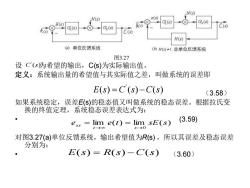
N(s N(s) (s) G,(s) (s (s H(s) @单位反馈系统 ()(s)≠1非单位反馈系统 图3.27 设C(s为希望的输出，Cs)为实际输出值。 定义：系统输出量的希望值与其实际值之差，叫做系统的误差即 E(s)=C(s)-C(s) (3.58) 如果系统稳定，误差E($)的稳态值又叫做系统的稳态误差。根据拉氏变 换的终值定理，系统稳态误差表达式为： ess=l。e(t)=limsE(s) (3.59) 对图3.27(a)单位反馈系统，输出希望值为R(s),所以其误差及稳态误差 分别为： E(S)=R(S)一C(S) (3.60)

设 为希望的输出，C(s)为实际输出值。 定义：系统输出量的希望值与其实际值之差，叫做系统的误差即 （3.58） 如果系统稳定，误差E(s)的稳态值又叫做系统的稳态误差。根据拉氏变 换的终值定理，系统稳态误差表达式为： • (3.59) 对图3.27(a)单位反馈系统，输出希望值为R(s) ，所以其误差及稳态误差 分别为： • （3.60） ' E s C s C s ( ) ( ) ( ) = − 图3.27 lim ( ) lim ( ) 0 e e t sE s t s s s → → = = E s R s C s ( ) ( ) ( ) = − ' C s( )

ess=lim sE(s)=lim s[R(s)-C(s)] 50 1 =ling$1+G(s) R(S) 式中，G(s)=G(s)G2(s)。 对图3.27(b)所示非单位反馈系统，将其进行结构等效变换成 单位反馈如图3.28所示。则其输出希望值为(s5,所 以其误差及稳态误差分别为： Es=R(-C()= 1R(S)-C(S) (3.62) H(s) 1 es =lim E(s)=lims- R(s) (3.63) 0°1+G(s) 1 lims 1R(S) 361+Gx(s)H(s) 式中， G(s)=G(s)G(s)H(s)

式中， 。 对图3.27(b)所示非单位反馈系统，将其进行结构等效变换成 单位反馈如图3.28所示。则其输出希望值为 ，所 以其误差及稳态误差分别为： （3.62） (3.63) 式中， 0 0 lim ( ) lim [ ( ) ( )] ss s s e sE s s R s C s → → = = − 0 1 lim ( ) s 1 ( ) k s R s → G s = + ( ) ( ) ( ) 1 2 G s G s G s k = ' 1 ( ) ( ) ( ) R s R s H s = ' 1 ( ) ( ) ( ) ( ) ( ) ( ) E s R s C s R s C s H s = − = − ' 0 0 1 lim ( ) lim ( ) 1 ( ) ss s s k e E s s R s → → G s = = + 0 1 1 lim ( ) 1 ( ) ( ) s k s R s → G s H s =  + ( ) ( ) ( ) ( ) 1 2 G s G s G s H s k =

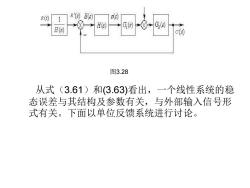
R(s) R'(s)E(s) G(s H(s) 图3.28 从式(3.61)和(3.63)看出，一个线性系统的稳 态误差与其结构及参数有关，与外部输入信号形 式有关。下面以单位反馈系统进行讨论

从式（3.61）和(3.63)看出，一个线性系统的稳 态误差与其结构及参数有关，与外部输入信号形 式有关。下面以单位反馈系统进行讨论。 图3.28

二.系统结构类型及开环增益 设单位反馈系统的开环传递函数为： G)= K(5+1).....(s+1)K(s+z).....(s+zm) S"(Ts+1)…(Tn-vS+I)S"(s+p)…(s+P-v) (3.64) G(s) K 式中，G(-+D…5+D当0，G0=l。 (Ts+1)…(Tmvs+'1) 从式(3.61)和(3.64)看出，系统稳态误差与其开环传递函数 有关，其实仅与G(s)中积分环节和K有关

二.系统结构类型及开环增益 设单位反馈系统的开环传递函数为: (3.64) 式中， ，当s→0，G0(0)=1。 从式(3.61)和(3.64)看出，系统稳态误差与其开环传递函数 有关，其实仅与Gk(s)中积分环节和K有关。 ( ) ( ) ( ) ( ) ( 1) ( 1) ( 1) ( 1) ( ) 1 * 1 1       − + − +  +  + = +  + +  + = n m n m k S s p s p K s z s z S T s T s K s s G s ( ) 0 G s S K  = ( 1) ( 1) ( 1) ( 1) ( ) 1 1 0 +  + +  + = − T s T s s s G s n m   

定义： 1.K定义为开环系统开环传递函数的增益，简称为系统开环 增益或开环放大倍数。也就是说，在G(S)中，除去积分环 节之外，令其s=0代入所得到的数值，称为开环增益。如 式(3.64)中，其开环增益就是K,即 K*I, K- I P (3.65) 2.式(3.65)中Y表示开环传函积分环节的个数。工程上以积 分环节个数来定义系统结构类型。即 ·Y=0,系统没有积分环节，称0型系统： ·y=1,系统有一个积分环节，称I型系统； y=2,系统有两个积分环节，称Ⅱ型系统

定义： 1.K定义为开环系统开环传递函数的增益，简称为系统开环 增益或开环放大倍数。也就是说，在Gk(s)中，除去积分环 节之外，令其s = 0代入所得到的数值，称为开环增益。如 式（3.64）中，其开环增益就是K，即 （3.65） 2. 式(3.65)中γ 表示开环传函积分环节的个数。工程上以积 分环节个数来定义系统结构类型。 即 • γ=0，系统没有积分环节，称0型系统； • γ=1，系统有一个积分环节，称Ⅰ型系统； • γ=2，系统有两个积分环节，称Ⅱ型系统。   − = = = n  i i m j j p K z K 1 1 *

三.给定稳态误差的计算 控制系统对给定输入信号R()作用下所产生的稳态误 差，称给定稳态误差。它反映了系统对给定输入信号在稳 态时的跟踪能力（跟踪精度）。下面我们应用静态误差系数 法，讨论不同典型给定输入时的给定稳态误差计算。 )为阶跃函数，即Rs)=,A为一常值。 根据式(3.61)得： 1 A A A es =lims. (3.66) 30 1+G(s)s 1+limG(s)1+K 5→0 武中，K,=mG,⑤)=m《,称静态位置误差系数。根据 式(3.66)有： 对于“0”型系统，Y=0,所以K=K,而稳态误 差 A ，是一个常数。可见ess减小必须增大开环 1+K 放大系数

三. 给定稳态误差的计算 控制系统对给定输入信号 作用下所产生的稳态误 差，称给定稳态误差。它反映了系统对给定输入信号在稳 态时的跟踪能力(跟踪精度)。下面我们应用静态误差系数 法，讨论不同典型给定输入时的给定稳态误差计算。 为阶跃函数，即 ，A为一常值。 根据式（3.61）得: (3.66) 式中， ，称静态位置误差系数。根据 式（3.66）有: 对于“0”型系统，γ=0 ，所以 Kp=K，而稳态误 差 ，是一个常数。可见ess减小必须增大开环 放大系数。 R t( ) R t( ) ( ) A R s s = 0 0 1 lim 1 ( ) 1 lim ( ) 1 ss s k k p s A A A e s → G s s G s K → =  = = + + +  S K K G s s k s p 0 0 lim ( ) lim → → = = 1 ss A e K = +

对于“I”型系统，，所以K=∞，稳态误差是零。同理，“Ⅱ” 型系统，稳态误差也是零。 “0”型系统稳态误差为常数，从物理意义上讲，如图3.29 所示的静态结构图可知，因系统没有积分环节，要维持系统 恒定输出，即 C(oo)=Kess 必然要存在一定恒定稳态误差，否则系统就没有输出。系统 的开环增益越大，稳态误差就越小。 c() 图3.29

对于“Ⅰ”型系统，，所以Kp=∞，稳态误差是零。同理，“Ⅱ” 型系统，稳态误差也是零。 “0”型系统稳态误差为常数，从物理意义上讲，如图3.29 所示的静态结构图可知，因系统没有积分环节，要维持系统 恒定输出，即 必然要存在一定恒定稳态误差，否则系统就没有输出。系统 的开环增益越大，稳态误差就越小。 ( ) C Ke  = ss 图3.29

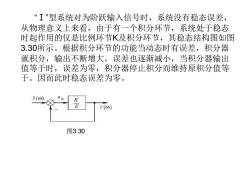
“工”型系统对为阶跃输入信号时，系统没有稳态误差， 从物理意义上来看，由于有一个积分环节，系统处于稳态 时起作用的仅是比例环节K及积分环节，其稳态结构图如图 3.30所示。根据积分环节的功能当动态时有误差，积分器 就积分，输出不断增大，误差也逐渐减小，当积分器输出 值等于时，误差为零，积分器停止积分而维持原积分值等 于。因而此时稳态误差为零。 C (co 图3.30

“Ⅰ”型系统对为阶跃输入信号时，系统没有稳态误差， 从物理意义上来看，由于有一个积分环节，系统处于稳态 时起作用的仅是比例环节K及积分环节，其稳态结构图如图 3.30所示。根据积分环节的功能当动态时有误差，积分器 就积分，输出不断增大，误差也逐渐减小，当积分器输出 值等于时，误差为零，积分器停止积分而维持原积分值等 于。因而此时稳态误差为零。 图3.30

R(s为斜坡输入，即 R(5)=- 根据式(3.61)时有： A A ess=lims- 、A 1+G(s)s2 limsG(s)Ky (3.67） K 式中K,=G)=g →0 (3.68)。 K称静态速度误差系数。 从式(3.67)及(3.68)不难看出： “0”型系统，Y=0,KV=0,稳态误差s=oo; “I”型系统，y=l,KV=const,.稳态误差es=l/KV,与K成反比； “IⅡ”型系统，y=2,KV=oo,其稳态误差es=0; 由此可见，“0”型系统在斜坡输入作用下，其=oo,表明0型 系统无法跟随斜坡输入信号

为斜坡输入，即 。 根据式（3.61）时有: (3.67) 式中 (3.68)。 KV称静态速度误差系数。 从式（3.67）及(3.68)不难看出: “0”型系统,γ=0, KV=0，稳态误差ess=∞； “Ⅰ”型系统,γ=1, KV=const, 稳态误差ess =1/KV, 与K成反比； “Ⅱ”型系统, γ=2, KV=∞，其稳态误差ess =0； 由此可见，“0”型系统在斜坡输入作用下，其ess =∞ ，表明0型 系统无法跟随斜坡输入信号。 R s( ) 2 ( ) A R s s = 2 0 0 1 lim 1 ( ) lim ( ) ss s k k V s A A A e s → G s s sG s K → =  = = + 1 0 0 lim ( ) lim → − → = =  S K K sG s s k s V