吉林大学：《自动控制原理》课程电子教案（PPT课件）第二章 控制系统数学模型 第一节 控制系统的时域数学模型

第二章 控制系统数学模型

控制系统数学模型 第二章

提要 1.描述系统各变量之间关系的数学表达式，叫做 系统的数学模型。实际存在的系统的动态性 能都可以通过数学模型来描述（例如微分方 程、传递函数等)。 2.建立合理的控制系统数学模型是控制系统分析 中最重要的内容，与系统性能密切相关。本 章将对系统和元件的数学模型建立、传递函 数概念、结构图和信号流图的建立及简化等 内容加以论述

提要 1.描述系统各变量之间关系的数学表达式，叫做 系统的数学模型。实际存在的系统的动态性 能都可以通过数学模型来描述（例如微分方 程、传递函数等）。 2.建立合理的控制系统数学模型是控制系统分析 中最重要的内容，与系统性能密切相关。本 章将对系统和元件的数学模型建立、传递函 数概念、结构图和信号流图的建立及简化等 内容加以论述

数学模型分为动态模型与静态模型。 a.控制系统的动态模型是指描述变量各阶导数之间关系的微分 方程。即线性定常微分方程，可由此分析系统的动态特性。 b.控制系统的静态模型是指在静态条件下（即变量的各阶导数 为零)，描述变量之间关系的代数方程。 建立系统数学模型时，必须： ()全面了解系统特性，确定研究目的以及准确性要求，决定 能否忽略一些次要因素而简化系统的数学模型。 (2)根据所应用的系统分析方法，建立相应形式的数学模型。 建立系统的数学模型主要有两条途径： 1.分析法。 2.实验法。即根据对系统的观察，通过测量所得到的输入、输 出数据，推断出系统的数学模型

数学模型分为动态模型与静态模型。 a.控制系统的动态模型是指描述变量各阶导数之间关系的微分 方程。即线性定常微分方程，可由此分析系统的动态特性。 b.控制系统的静态模型是指在静态条件下（即变量的各阶导数 为零），描述变量之间关系的代数方程。 建立系统数学模型时，必须： (1) 全面了解系统特性，确定研究目的以及准确性要求，决定 能否忽略一些次要因素而简化系统的数学模型。 (2) 根据所应用的系统分析方法，建立相应形式的数学模型。 建立系统的数学模型主要有两条途径： 1.分析法。 2.实验法。即根据对系统的观察，通过测量所得到的输入、输 出数据，推断出系统的数学模型

第一节控制系统的时域数学模型 控制系统的运动状态和动态性能可由微分方程 式描述，微分方程式是系统的一种数学模型。建立 系统微分方程的一般步骤如下： (1)适当简化，忽略一些次要因素。 (2)根据元件的物理或化学定律，列出相应的微分 方程式。 (③)消去中间变量，推出元件的输入量和输出变量 之间关系的微分方程。 (4)求出其它元件的方程。 (⑤)从所有元件的方程式中消去中间变量，最后得 到系统的输入输出微分方程

第一节 控制系统的时域数学模型 控制系统的运动状态和动态性能可由微分方程 式描述，微分方程式是系统的一种数学模型。建立 系统微分方程的一般步骤如下： (1) 适当简化，忽略一些次要因素。 (2) 根据元件的物理或化学定律，列出相应的微分 方程式。 (3) 消去中间变量，推出元件的输入量和输出变量 之间关系的微分方程。 (4) 求出其它元件的方程。 (5) 从所有元件的方程式中消去中间变量，最后得 到系统的输入输出微分方程

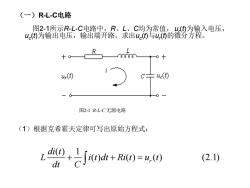
(一)RL-C电路 图2-1所示R-L-C电路中，R、L、,C均为常值，U(⑤为输入电压， u()为输出电压，输出端开路。求出u)与u①的微汾方程。 十0 () ud(t) 图2-1R-L-C无源电路 (1)根据克希霍夫定律可写出原始方程式： i+i0ot+0=e0 (2.1)

（一）R-L-C电路 图2-1所示R-L-C电路中，R、L、C均为常值，ur (t)为输入电压， uc (t)为输出电压，输出端开路。求出uc (t)与ur (t)的微分方程。 （1）根据克希霍夫定律可写出原始方程式： 图2-1 R-L-C 无源电路 ( ) 1 ( ) ( ) ( ) (2.1) r di t L i t dt Ri t u t dt C + + = 

(2)式中(t)是中间变量，它与输出u.(t)有如下关系： .(=ja (2.2) (3)消去式(2.1)、式(2.2)的中间变量()后，输入输出 微分方程式： du(t) dt2 +RC du (t) 2+u.(t)=u,(t) dt (2.3) 或 d@+x du (t) dt2 dt 2+u.(0)=4,( (2.4) 式中T=LC,T,=RC为电路的时间常数，单位为秒。 式(2.3)和式(2.4)是线性定常二线性微分方程

（2）式中i(t)是中间变量，它与输出uc (t)有如下关系： (3) 消去式(2.1)、式(2.2)的中间变量i(t)后，输入输出 微分方程式： 2 2 d ( ) d ( ) ( ) ( ) d d c c c r u t u t LC RC u t u t t t + + = 或 (2.4) (2.3） 式中T1 =LC，T2 =RC为电路的时间常数，单位为秒。 式(2.3)和式(2.4)是线性定常二阶线性微分方程。 1 ( ) ( )d c u t i t t C =  1 ( ) ( )d (2.2) u t i t t c C =  2 1 2 2 d ( ) d ( ) ( ) ( ) d d c c c r u t u t T T u t u t t t + + =

二、非线性方程的线性化 几乎所有元件或系统的运动方程都是非线性的。 但对于较小的范围内的运动，把这些元件看作是线性 元件，因此可以建立线性微分方程。线性微分方程， 满足迭加原理和齐次性。 研究非线性系统在某一工作点（平衡点）附近的 性能，（如图2-2，X为平衡点，受到扰动后，(）偏 离xo,产生△x(),△X)的变化过程，表征系统在X附 近的性能) 可用下述的线性化方法得到的线性模型代替非线 性模型来描述系统： 图2-2小偏差过程

二、非线性方程的线性化 几乎所有元件或系统的运动方程都是非线性的。 但对于较小的范围内的运动，把这些元件看作是线性 元件，因此可以建立线性微分方程。线性微分方程， 满足迭加原理和齐次性。 研究非线性系统在某一工作点（平衡点）附近的 性能，（如图2-2，x0为平衡点，受到扰动后，x(t)偏 离x 0，产生Δx(t)，Δx(t)的变化过程，表征系统在x0附 近的性能） 可用下述的线性化方法得到的线性模型代替非线 性模型来描述系统： 图2-2 小偏差过程

设连续变化的非线性函数为y=x)。取某平衡状态A为工作 点，即=fxo)当x=x+Ax时，y=+ 设函数fx)在x,) 连续可微，则在该点附近用泰勒级数展开为： y=w)=f(x,)+( d l (x-x> 1 d'f(x) 2！dx2 21(x-x) (2.5) 当(x-x)很小时，略去高次幂相，则 y-%=f)-fx,)= (x-xo> d (2.6) 则略去增量符Ay=K△x,or,y=K,附近的线性化方程 令Ay=y-=f(x)-f(xo), △x=(x-xo), K- af(x) dx

(2.5) 当 很小时，略去高次幂相，则 (2.6) 则略去增量符号，可得到在工作点附近的线性化方程 设连续变化的非线性函数为y = f(x)。取某平衡状态A为工作 点，即 。当 时， ，设函数f(x)在 连续可微，则在该点附近用泰勒级数展开为： 0 (x x − ） 0 0 0 ( ) ( ) ( ), ( df x y y y f x f x x x x K dx 令 ）,  = − = −  = − = 0 0 0 0 ( ) ( ) ( ) | ( x df x y y f x f x x x dx − = − = − ） 0 0 2 0 0 0 2 ( ) ( ) ( ) ( ) | ( | ( x x df x d f x y f x f x x x x x dx dx = = + − − + ）+ ） 1 2 2！  =  = y K x or y Kx , , , 0 0 y f x = ( ) 0 x x = + x 0 y y y = + 0 0 ( , x y )

y=f) u.(1 u(t) 图2-3小偏差线性化示意图 图2-4 RL网络 例2-3，设铁芯线圈电路如图2-4所示，其磁通与线圈中电 流之间的关系如图2-5所示，试写出以为输入，为输出的 微分方程。 解(1)设铁芯线圈磁通 变化时产生的感应电势为： 图2-5磁通与线圈中电流之间的关系

2 0 0 2 d d ( ) ( ) d d f f i i   , , Rn+1  0 f 0 i 图2-3 小偏差线性化示意图 图2-4 RL网络 例2-3，设铁芯线圈电路如图2-4所示，其磁通与线圈中电 流之间的关系如图2-5所示，试写出以为输入，为输出的 微分方程。 解（1）设铁芯线圈磁通 变化时产生的感应电势为： 图2-5磁通与线圈中电流之间的关系

U。=K1 do(i) (2.7) dt (2)电路微分方程为： dp(i) +Ri=K dp(i)di U.=K i +Ri dt di dt 设在平衡点的邻域内，p对的各阶导数（直至n+1) 是存在的，它可展成泰勒级数： do(i) p()=0()+( (△)2+… (2.8) 其中：△i=i-i0 当△i足够小时，略去高阶导数 p()-p(i)=( o@).△i=KA di

1 1 ( ) ( ) r d i d i di U K Ri K Ri dt di dt   = + = + （2）电路微分方程为： 设在平衡点的邻域内，  对i的各阶导数（直至n+1） 是存在的，它可展成泰勒级数： 0 0 2 2 0 2 ( ) 1 ( ) ( ) ( ) ( ) ( ) 2 ! i i d i d i i i i di di    = +  +  + (2.7) (2.8) 1 d i( ) U K dt   = 其中：Δi =i- i 0 当Δi 足够小时，略去高阶导数 0 0 ( ) ( ) ( ) ( )i d i i i i K i di   − =  = 