《计算机应用基础》课程教学资源（PPT课件讲稿）第四章 数制与信息编码

山求程王大彩 SHANDONG UNIVERSITY OF TECHNOLOGY 第二篇系统平台与计算环境 第4章数制与信息编码

第二篇系统平台与计算环境 第4章数制与信息编码

0 目录 什草凤利学与拉未学脑 数制及其转换 数值型数据的表示及处理 3. 文字的表示及处理 多媒体信息的表示及处理 5. 条形码和RFID

目录 4. 多媒体信息的表示及处理 3. 文字的表示及处理 2. 数值型数据的表示及处理 1. 数制及其转换 5. 条形码和RFID

计算机中信息的表示 林草机利学与技未学 计算机最主要的功能就是处理信息，而信息在 计算机中如何表示、存放、传递？这是首先要 解决的问题。 n 基本要求是：信息的表示、存放和传递要方便、 可靠、易处理。 显然，在计算机内部，信息只有经过数字化编 码后才能表示、存放和传递。 所谓编码，就是用少量的基本符号，根据简单 的组合规则，以表示大量复杂的信息。 二进制是一种最简单的编码系统

◼ 计算机最主要的功能就是处理信息，而信息在 计算机中如何表示、存放、传递？这是首先要 解决的问题。 ◼ 基本要求是：信息的表示、存放和传递要方便、 可靠、易处理。 ◼ 显然，在计算机内部，信息只有经过数字化编 码后才能表示、存放和传递。 ◼ 所谓编码，就是用少量的基本符号，根据简单 的组合规则，以表示大量复杂的信息。 ◼ 二进制是一种最简单的编码系统。 计算机中信息的表示

0 什草凤利学与拉未学脑 ·计算机中的信息采用二进制编码来表示。 二进制表示数字在物理上最容易实现（只有0、1）， 与电子部件的二态性相对应。 口二进制运算规则简单（逢二进一）。 口二进制数可以直接进行逻辑运算

◼ 计算机中的信息采用二进制编码来表示。 ❑ 二进制表示数字在物理上最容易实现(只有0、1), 与电子部件的二态性相对应。 ❑ 二进制运算规则简单（逢二进一）。 ❑ 二进制数可以直接进行逻辑运算

0 计草机利学与校术学网 乾 三三 三三 三三 邮

1.数制及其转换 0 件菜凤利学与拉未学腐 口常用数制 口数制的转换 口二进制的运算规则

1.数制及其转换 ❑ 常用数制 ❑ 数制的转换 ❑ 二进制的运算规则

数制及其转换 数制的概念 数制(Numbering system)即表示数值的方法，有 非进位数制和进位数制两种。 ■表示数值的数码与它在数中的位置无关的数制称为 非进位数制。 ■按进位的原则进行计数的数制称为进位数制，简称 “进制

数制及其转换 数制的概念 数制（Numbering system）即表示数值的方法，有 非进位数制和进位数制两种。 ◼ 表示数值的数码与它在数中的位置无关的数制称为 非进位数制。 ◼ 按进位的原则进行计数的数制称为进位数制，简称 “进制”

几个名词术语 什草凤利学与拉未学脑 ·数码：一组用来表示某种数制的符号。如：1、2、3、 4、A、B、C等。 ■基数：数制所使用的数码个数称为“基数” 或 “基”，常用“R”表示，称R进制。如二进制的数码 是：0、1，基为2。 ■位权：指数码在不同位置上的权值。在进位计数制中， 处于不同数位的数码，代表的数值不同

几个名词术语 ◼ 数码：一组用来表示某种数制的符号。如： 1、2、3、 4、A、B、C等。 ◼ 基数：数制所使用的数码个数称为“基数” 或 “基”，常用“R”表示，称R进制。如二进制的数码 是：0、1，基为2。 ◼ 位权：指数码在不同位置上的权值。在进位计数制中， 处于不同数位的数码，代表的数值不同

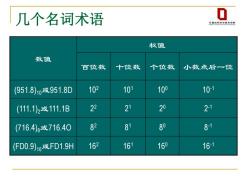
几个名词术语 0 计草机利学与校术学腐 权值 数值 百位数 十位数 个位数 小数点后一位 (951.8)10或951.8D 102 101 100 10-1 (111.1)2或111.1B 22 21 20 21 (716.4)8或716.40 82 81 80 81 (FD0.9)16或FD1.9H 162 161 160 161

几个名词术语 数值 权值 百位数 十位数 个位数 小数点后一位 (951.8)10或951.8D 102 101 100 10-1 (111.1)2或111.1B 2 2 2 1 2 0 2 -1 (716.4)8或716.4O 8 2 8 1 8 0 8 -1 (FD0.9)16或FD1.9H 162 161 160 16-1

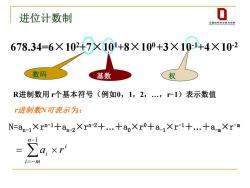
进位计数制 什草凤利学与拉未学脑 678.34=6×1024⑦×⑩+8×100+3×1044×10-2 数码 基数 权 R进制数用个基本符号（例如0,1,2，一1)表示数值 r进制数N可表示为： N=an-1Xrm-1+an-2Xr-2+.+aoXr0+a_1Xr-1+.+a-Xrm

进位计数制 =  =− − a r i i m n i 1 N=an-1×r n-1＋an-2×r n-2＋.＋a0×r 0＋a-1×r -1＋.＋a-m×r -m r进制数N可表示 为： R进制数用 r个基本符号（例如0，1，2，.，r-1）表示数值 数码 基数 权 678.34=6×102+7×101+8×100 +3×10-1+4×10-2