西安电子科技大学：《数字信号处理》课程教学课件（讲稿）02 时域离散信号和系统的频域分析（1/2）

本章主要内容 序列的傅里叶变换(DTFT) 离散傅里叶级数(DFS) 周期序列的傅里叶变换 序列的Z变换(ZT) 逆Z变换(IZT) 时域离散时不变系统的变换域分析 梳状滤波器 2

本章主要内容  序列的傅里叶变换 （DTFT ）  离散傅 叶级数 里 （DFS ）  周期序列的傅里叶变换  序列的 Z变换 （ZT ）  逆 Z变换 （IZT ）  时域离散时不变系统的变换域分析  梳状滤波 器 2

2.1引言 ■信号和系统的分析工具 口时域 ■直观 ■求解难，分析困难 ■特征不易把握 ■设计难 口频域 ■便于求解 ■分析、设计易

2 1. 引言  信号和系统的分析 具 信号和系统的分析工具  时域  直观  求解难，分析困难  特征不易把握  设计难  频域  便于求解  分析 设计易 3

频域分析的数学工具 ■模拟连续信号 口傅里叶变换→拉普拉斯变换 ■时域离散信号 口傅里叶变换→Z变换 口傅里叶变换： 时域→实频域 口Z变换： 时域→复频域

频域分析的数学工具  模拟连续信号  傅里叶变换  拉普拉斯变换  时域离散信号  傅里叶变换  Z变换  傅里叶变换： 时域 实频域  Z变换： 时域 复频域 4

回顾：信号分解 ■目的 ■基本分解函数的选择 口时域：冲激函数/单位脉冲序列 口频域：正弦函数（序列）/复指数函数 ■傅里叶级数 ■傅里叶变换

回顾：信号分解  目的  基本分解函数的选择  时域：冲激函数 / 单位脉冲序列  频域：正弦函数（序列）/ 复指数函数  傅里叶级数  傅里叶变换 5

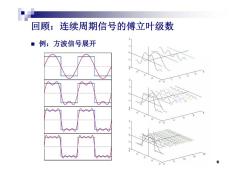
回顾：连续周期信号的傅立叶级数 ■例：方波信号展开

回顾：连续周期信号的傅立叶级数  例：方波信号展开 6

回顾：连续周期信号的傅立叶级数 ■例：方波信号展开 豫 时诚图 像 15 10 摩前一〉 7

回顾：连续周期信号的傅立叶级数  例：方波信号展开 7

回顾：连续周期信号的傅立叶级数 https://en.wikipedia.org/wiki/Fourier series Function s(x)(in red)is a sum of six sine functions of different amplitudes and harmonically related frequencies.Their summation is called a Fourier series The Fourier transform,S(f) (in blue),which depicts amplitude vs frequency, reveals the 6 frequencies (at odd harmonics)and their amplitudes(1/odd number). ·推荐：[知乎]傅里叶分析之掐死教程（完整版）https:zhuanlan.zhihu.comp/19763358

回顾：连续周期信号的傅立叶级数 https://en.wikipedia.org/wiki/Fourier_series Function s(x) (in red) is a sum of six sine functions of different amplitudes and harmonically related frequencies. Their summation is called a Fourier series. The Fourier transform, S(f) (in blue), which depicts amplitude vs frequency, reveals the 6 frequencies (at odd harmonics) and their amplitudes (1/odd number). 8 • 推荐：[知乎] 傅里叶分析之掐死教程（完整版） https://zhuanlan.zhihu.com/p/19763358

回顾：连续周期信号的傅立叶级数 ·正变换（分解）Xu2,)=值0ead= ■反变换（合成） 0)=∑X(Um2)ee 20= 2π To ■时域周期信号，频域离散频谱(T越大，频谱越稠密) ■任意周期信号x()可分解为无穷多个不同频率的复指数 信号之和，即直流分量和各次谐波分量。·（物理含义） x(t) 0 -To 2π 9

回顾：连续周期信号的傅立叶级数  正变换（分解） 0 0 0 0 j j 2 0 1 ( ) ( ) ( ), T n t n T t X n x t e dt t x e T            反变换（合成） 0 2T 0   0 j () ( ) n t x t jn X e       0 0 2 T   时域周期信号，频域离散频谱（T0越大，频谱越稠密） T0 0 n   任意周期信号 可分解为无穷多个不同频率的复指数 信号之和，即直流分量和各次谐波分量。-（物理含义） x t ( ) 0 x ( )t X jn ( )   - - 9 0 0 2 T     T0 t 0 0

回顾：连续非周期信号的傅立叶变换 ■正变换 X(j)=[x(t)edr ■反变换 x0=是∫x(U2-ed2 2π ■ 时域非周期绝对可积信号， 里叶级 巾口 频域连续频谱 H 博里叶变换 结论： ■时域连续周期→频域离散非周期 ■时域连续非周期→频域连续非周期 10

回顾：连续非周期信号的傅立叶变换  正变换 j ( ) () t X j x t e dt       正变换   反变换 1 j () ( ) 2 t x t X j d e        ( ) () j   时域非周期绝对可积信号， 2  频域连续频谱 结论：  时域连续周期  频域离散非周期  时域连续非周期  频域连续非周期 10

2.2时域离散信号的傅里叶变换 ■时域离散信号的傅里叶变换(DTFT)的定义 ■周期信号的离散傅里叶级数(DFS) ■周期信号的傅里叶变换 ■时域离散信号傅里叶变换的性质

2 2. 时域离散信号的傅里叶变换  时域离散信号的傅里叶变换（DTFT）的定义  周期信号的离散傅里叶级数（DFS）  周期信号的傅里叶变换  时域离散信号傅里叶变换的性质 11