西安电子科技大学：《高等微波网络》课程教学课件（讲稿）15 Chebyshev综合

15.Chebyshev综合 西安电子科技大学，电子工程学院

15. Chebyshev 综 合 西安电子科技大学，电子工程学院 苏 涛

Butterworth综合 G Hn 带外过于平坦 。 H/2 n=3 ·带边3dB n= Go2） H 2n

G f wc Hn Hn 2 n = 3 n = 5 Butterworth综合 ( ) n c Hn G 2 2 1 ÷ ÷ ø ö ç ç è æ + = w w w • 带外过于平坦 • 带边3dB

15.Chebyshev综合 一、 Chebyshev函数 二、Chebyshev多项式逼近 三、修正的偶数阶Chebyshev函数 四、Chebyshev综合

15. Chebyshev 综 合 一、Chebyshev函数 二、Chebyshev多项式逼近 三、修正的偶数阶Chebyshev函数 四、Chebyshev综合

15.Chebyshev综合 一、Chebyshev函数 二、Chebyshev多项式逼近 三、修正的偶数阶Chebyshev函数 四、Chebyshev综合

15. Chebyshev 综 合 一、Chebyshev函数 二、Chebyshev多项式逼近 三、修正的偶数阶Chebyshev函数 四、Chebyshev综合

Chebyshev函数 T()= cosn-cosx)≤】 chn-chx) x>1 (1)表面分段，实质连续； (2)表面超越函数，实际是整数多项式； (3)带内等波纹，带外单调；

( ) ( ) ï ( ) î ï í ì × > × £ = - - 1 cos cos 1 1 1 ch n ch x x n x x T x n Chebyshev函数 （1）表面分段，实质连续； （2）表面超越函数，实际是整数多项式； （3）带内等波纹，带外单调；

递推公式 T)=2xT,()-T(x) T,=1 T=x 证明： a =cos-x x=cosa cos(n+1a+cos(n-1)a=2cosa cosna T(x)+T(x)=2xT (x)

递推公式 ( ) ( ) ( ) T x T T x xT x T x n n n = = + = - - 1 0 1 1 1 2 证明： x 1 cos- a = x = cosa cos(n +1)a + cos(n -1)a = 2cosa cos na T (x) T (x) xT (x) n n n 2 +1 + -1 =

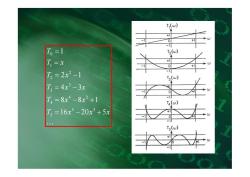
T(w) T,=1 T2(w） T=x +1 T3=2x2-1 3w) T3=4x3-3x T4=8x4-8x2+1 T=16x3-20x3+5x Ts(w)

L T x x x T x x T x x T x T x T 16 20 5 8 8 1 4 3 2 1 1 5 3 5 4 2 4 3 3 2 2 1 0 = - + = - + = - = - = =

(1)零点特性 1) neven 10 (2)带边特性 置 T@0=1 (3)奇偶特性 T,(-x)=()T.(x)

（1）零点特性 ( ) ( ) î í ì - = n odd n even T n n 0 1 0 2 （2）带边特性 (1) =1 Tn （3）奇偶特性 T ( x) ( ) T (x) n n n - = -1

(4)带外特性 道道 带外单调变化 (5)最佳特性 2'“事 当x=xn处，T.)=P6) 若带外固定，则Chebyshev带内波纹最小； 若带内波纹固定，则Chebyshev带外最陡

（4）带外特性 带外单调变化 ( ) 2 1 1 » >> - T x x x n n n （5）最佳特性 当 x = xm 处， ( ) ( ) n m n m T x = P x 若带外固定，则Chebyshev带内波纹最小； 若带内波纹固定，则Chebyshev带外最陡

15.Chebyshev综合 一、 Chebyshev函数 三、Chebyshev多项式逼近 三、修正的偶数阶Chebyshev函数 四、Chebyshev综合

15. Chebyshev 综 合 一、Chebyshev函数 二、Chebyshev多项式逼近 三、修正的偶数阶Chebyshev函数 四、Chebyshev综合