西安电子科技大学:《数字信号处理》课程教学课件(讲稿)03 离散傅里叶变换DFT及其快速算法FFT

问题: ■序列的傅里叶变换、Z变换是时域离散信号及系统分析与 设计的重要数学工具; ■但变换结果均为连续函数,无法用计算机进行处理; ■离散傅里叶变换(DFT)对有限长时域离散信号的频谱进 行等间隔采样,频域函数被离散化了,便于信号的计算机 处理。 ■DFT运算量较大,快速离散傅里叶变换算法(FFT)是解 决方案 2
问题: 序列的傅里叶变换、Z变换是时域离散信号及系统分析与 设计的重要数学工具; 但变换结果均为连续函数,无法用计算机进行处理; 离散傅里叶变换(DFT)对有限长时域离散信号的频谱进 行等间隔采样,频域函数被离散化了,便于信号的计算机 处理。 DFT运算量较大,快速离散傅里叶变换算法(FFT)是解 决方案 2
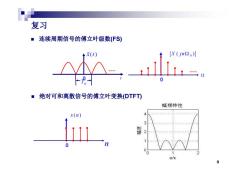
复习 ■连续周期信号的傅立叶级数(FS) x(jn2o)川 ■绝对可和离散信号的傅立叶变换(DTFT) 幅频特性 7 o/n 3
复习 连续周期信号的傅立叶级数(FS) 0 x ( )t X jn ( ) - T00 t 0 - 绝对可和离散信号的傅立叶变换(DTFT) x ( ) n 0 n 3
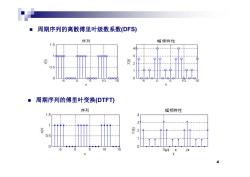
◆ 周期序列的离散傅里叶级数系数(DFS) 序列 幅频特性 15 -5 10 ■周期序列的傅里叶变换(DTFT) 序列 幅频特性 1.5 10 0/4
周期序列的离散傅里叶级数系数(DFS) 周期序列的傅里叶变换(DTFT) 4

3.1离散傅里叶变换(DFT)的定义 ■3.1.1DFT的定义 设xn)是一个长度为M的有限长序列,)的N点离散傅立叶变换: XW=DFT(-∑0me号 N 0≤k≤N-1 三0 口N称为DFT变换区间长度,N≥M ·令w=e贤 (简化书写) ■离散傅立叶变换与逆变换对为: X)=DFTO])-分0mw0≤k≤N-1 n=0 o=Tx-三r传g 0≤n≤N-1
3.1离散傅里叶变换 离散傅里叶变换( ) DFT 的定义 3.1.1 DFT的定义 设x(n)是一个长度为M的有限长序列,x(n)的N点离散傅立叶变换: 1 2j ( ) [ ( )] ( )e 0 1 N kn N X k DFT x n x n k N N称为DFT变换区间长度, 0 ( ) [ ( )] ( )e 0 1 N n X k DFT x n x n k N N M 令 (简化书写) 离散傅立叶变换与逆变换对为: 2j N W e N 离散傅立叶变换与逆变换对为: 1 ( ) [ ( )] ( ) 0 1 N kn X k DFT x n x n W k N N 0 N n 1 1 ( ) [ ( )] ( ) 0 1 N kn N x n IDFT X k X k W n N N 5 0 N N k

X(A)-DFTI-0sN-1 证明: DFTx=芝Xkw N K=0 x(m)WkW Nk=0 m=0 N-I 1 N-I wk(m-n) 由于 W)= 1, m-n=MN,M为整数 e N 0, m-n≠MN,M为整数 于是 N- IDFT[X(k)]=∑x(m)6(m-m)=x(n)0≤n≤N-1 m=0 因此离散傅立叶逆变换是唯一的 6
证明 N -1 1 kn 1 0 ( ) [ ( )] ( ) 0 1 N kn N n X k DFT x n x n W k N 证明: IDFT[ ] ( ) -kn N k=0 1 X(k) X k W N -1 1 1 [ ] N N- mk -kn ( )W W =0 =0 [ ] mk kn N N k m x(m)W W N ( ) ( ) N -1 N -1 1 k m-n xm W 由于 ( ) N m=0 k=0 xm W N 由于 N1 1 2 ( ) ( ) k0 0 1 0 N j km n k m-n N N k 1 1 m n MN,M W e= N N m n MN,M , 为整数 , 为整数 于是 1 IDFT[ ( )]= ( ) ( ) N X k xm m n xn n N () 0 1 因此离散傅立叶逆变换是唯一的 m0 xn n N () 0 1 6 因此离散傅 叶逆变换是唯 的

例3.1.1 x(n)=R(n)分别计算序列的8点、16点DFT 解:8点DFT x)-立Rw-2e5 8k=0 0k=1,2,3,.,7 16点DFT -2k8 X()-R()R 1-W 1-e ,πk -jk 1=eke/2(e2=e2 e语sin _=e 2 1-ee(e-e π sin 16 k=0,1,2,.,15
例3.1.1 x() () n Rn 8 分别计算序列的 分别计算序列的8点、16点DFT 解: 8点DFT 7 8 8 () () kn X k R nW 8 7 2 8 j kn e 8 8 n0 n0 8 0 k 16点DFT 0 1, 2, 3, , 7 k 16点DFT 15 7 8 16 8 16 () () () kn kn X k R nW R nW 2 8 16 2 1 j k e 8 16 1 k k W 8 16 8 16 0 0 () () () n n 2 16 1 j k e 16 1 k W 7 sin kk k jj j j k k 7 22 2 16 8 16 16 16 sin 1 () 2 1 ( ) sin 16 jj j j k j k jk j k j k j k k e ee e e e ee e k 7 ( ) 16 0, 1, 2, , 15 e ee e k
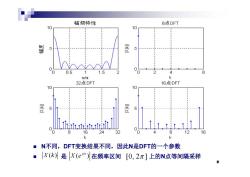
幅频特性 8点DFT 10 5 爱 5 0 0.5 1 1.5 0 /r k 32点DFT 16点DFT 10 10 5 w.o. 8 1624 32 8 12 1日 ■N不同,DFT变换结果不同,因此N是DFT的一个参数 ■X(k)是X(eo)在频率区间[0,2π]上的N点等间隔采样 8
N不同,DFT变换结果不同,因此 N 是DFT 的 一个参数 8 X k( ) 是 在频率区间 上的 ( ) N点等间隔采样 j X e [0, 2 ] 不同 变换结果不同 因此 是 的 个参数

3.1.2DFT与FT、ZT、DFS之间的关系 1.DFT与FT、ZT之间的关系 ■有限长序列 x(n) n=0,1,2,.M-1 N≥M ■DFT与FT、ZT (k)=DFTLx(a)(n)e M-1 0≤k≤N-1 i=0 Ke)=ZIx1=2m-”=2m= M- X(e)=FT[x(nl=∑xn)em=∑x(n)e- X(k)=X(e儿÷,X(k)=X(eo)儿a-k' 0≤k≤N-1 9
3.1.2 DFT与FT、ZT、DFS之间的关系 1. DFT与FT、ZT之间的关系 3 与 、 、 S之间的关系 有限长序列 xn n M ( ) 0,1,2, 1 N M DFT与FT、ZT ( ) 1 2j M kn 1 ( ) [ ( )] ( ) ( ) M n n j 0 ( ) [ ( )] ( )e 0 1 kn N N n X k DFT xn xn k N 0 ( ) [ ( )] ( ) ( ) n n n n X z ZT x n x n z x n z 1 ( ) [ ( )] ( ) ( ) M j jn jn 2 ( ) ( ) ( ) ( )| 0 1 j Xk X Xk X k N 0 ( ) [ ( )] ( ) ( ) j jn jn n n X e FT x n x n e x n e 9 2 () () ( ) ( )| 0 1 2 j k N N j z e k Xk X z Xk X e k N , ,
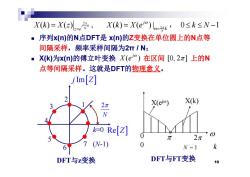
X(k)=X(e÷,X(k)=X(eo)儿ak, 0≤k≤N-1 ■序列x《)的N点DFT是xn)的Z变换在单位圆上的N点等 间隔采样,频率采样间隔为2T/N; ■X(k)为xn)的傅立叶变换X(e)在区间[0,2π]上的N 点等间隔采样。这就是DFT的物理意义。 jIm[z] 2π X(eio) X(k) K=0 Re[Z] 2π 6 (N-1) 0 N-1 DFT与z变换 DFT与FT变换 10
2 () () j k N ( ) ( )| 2 0 1 j k Xk Xz Xk Xe k N , , 序列x(n)的N点DFT是 x(n)的Z变换在单位圆上的N点等 间隔采样 频率采样间隔为2π / N; ( ) ( ) ( ) ( )| N 2 N z e k 间隔采样,频率采样间隔为2π / N; X(k)为x(n)的傅立叶变换 在区间 上的N 点等间隔采样 这就是DFT的物理意义 ( ) [0, 2 ] j X e j Z Im 点等间隔采样。这就是DFT的物理意义。 X(ejω) X(k) 1 2 3 2 R Z 3 4 N k 0 2 o 0 N 1 k 0 ReZ 5 6 7 (N-1) k=0 DFT与z变换 10 6 N 1 k DFT与FT变换

3.1.2DFT与DFS、ZT、FT之间的关系 2.DFT与DFS之间的关系 ■有限长序列 x(n)n=0,1,2,.M-1 ■将x)以N为周期进行周期延拓,得到周期序列 v(n)=∑x(n+mW)=x(n)w m=- xx(n)=x(n)Rv (n) 显然,当 N≥M,x(n)=x(n) xv(n)是x(n)的周期延拓序列 x(n)是xv(n)的主值区间序列 11
3.1.2 DFT与DFS、ZT、FT之间的关系 2. DFT与DFS之间的关系 有限长序列 将 以 为周期进行周期 拓 得到周期序列 xn n M ( ) 0,1,2, 1 将x(n)以N为周期进行周期延拓,得到周期序列 x n x n mN x n ( ) ( ) (( )) N N ( ) ( ) (( )) m x n x n mN x n () () () N NN x n x nR n 显然,当 () () () N NN x n x nR n , () () N M x n xn N x n N ( ) 是 的周期延拓序列 x( ) n 11 x( ) n 是 的主值区间序列 ( ) Nx n
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)02 时域离散信号和系统的频域分析(2/2).pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)02 时域离散信号和系统的频域分析(1/2).pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)02 时域离散信号与系统 Discrete-Time Signals and Systems in the Time-Domain.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)01 绪论(主讲:王柯俨).pdf
- 《机械工程学报》:抛物面索网天线的最佳型面设计方法(西安电子科技大学:杨东武、尤国强、保宏).pdf
- 机械电子工程中的科学计算方法(文献资料)卫星与天线相对位置 PIM CHARACTERISTICS OF THE LARGE DEPLOYABLE REFLECTOR ANTENNA MESH.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)24 总结.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)23 匹配网络设计.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)22 General Chebyshev综合.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)21 耦合谐振腔电路和耦合矩阵.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)20 交叉耦合滤波器总览.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)19 倒置变换器和微波滤波器电路.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)18 公比线带通滤波器.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)17 半集总元件微波滤波器.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)16 低通原型和滤波器原理电路综合.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)15 Chebyshev综合.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)14 Butterworth综合.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)13 网络综合概述.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)12 多模网络和模式匹配法.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)11 对称网络和奇偶模法.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)04 模拟信号数字处理.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)05 数字滤波器的基本概念及一些特殊滤波器.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)06 IIR数字滤波器(IIRDF)设计.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)07 FIR数字滤波器(FIRDF)设计.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)08 时域离散系统的实现.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)09 多采样率数字信号处理.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第一部分 概述 第1章 绪论(主讲:权义宁).pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第一部分 概述 第2章 网络模型.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 物理层和介质 第3章 物理层——数据和信号.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第4章 数字传输 Digital Transmission.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第5章 模拟传输 Analog Transmission.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第6章 带宽利用 Bandwidth Utilization:Multiplexing and Spreading.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第7章 传输介质.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第8章 交换.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第9章 使用电话网和有线电视网进行数据传输.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第10章 检错与纠错 Error Detection and Correction.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第11章 数据链路控制 Data Link Control.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第12章 多路访问 Multiple Access.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第13章 有线局域网——以太网.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第14章 无线局域网.pdf
