西安电子科技大学：《数字信号处理》课程教学课件（讲稿）08 时域离散系统的实现

8.1引言 ■时域离散系统的实现方式 口软件实现 口硬件实现 ■数字滤波器的表示方法 口数字滤波器的系统函数： b26 H(2)= Y() k=0 X(2) 1+

8 1. 引言  时域离散系统的实现方式  软件实现  硬件实现  数字滤波器的表示方法  数字滤波器的系统函数： 0 ( ) ( ) M k k k b z Y z H    0 1 ( ) ( ) ( ) 1 k N k k k H z X z a z      k1 2

■数字滤波器的表示方法 口常系数线性差分方程： m)=-∑an-)+6，xn-k) k- k=0 ■均由延迟、乘法、加法实现 ■滤波器的不同实现算法、运算结构网络结构 口计算误差（有限字长效应） 口计算复杂度（乘法、加法、存取数、比较数的次数） 口存储量（系统参数、中间结果、输入输出信号值等) 口计算速度

 数字滤波器的表示方法  常系数线性差分方程: () ( ) ( ) N M k k yn ayn k bxn k        均由延迟、乘法、加法实现 k k 1 0  滤波器的不同实现算法、运算结构/网络结构  计算误差 （有限字长效应）  计算复杂度（乘法、加法、存取数、比较数的次数）  存储量（系统参数、中间结果、输入输出信号值等）  计算速度 3

本章内容 ■理解数字滤波器结构的表示方法 ■掌握R滤波器的基本结构：直接型、级联型、并联型 ■掌握FIR滤波器的直接型、级联型、线性相位结构，理解 频率抽样型结构 ■了解数字滤波器的格型结构

本章内容  理解数字滤波器结构的表示方法  掌握IIR滤波器的基本结构：直接型、级联型、并联型  掌握FIR滤波器的直接型、级联型、线性相位结构，理解 频率抽样型结构  了解数字滤波器的格型结构 4

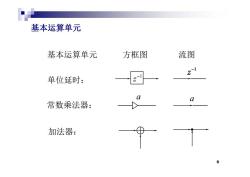
基本运算单元 基本运算单元 方框图 流图 2-1 单位延时： 常数乘法器： 加法器：

基本运算单元 基本运算单元 方框图 流图 1 z  单位延时： a a 常数乘法器： 加法器： 5

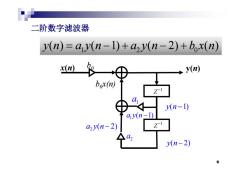
二阶数字滤波器 y(n)=ay(n-1)+azy(n-2)+box(n) →⊕ y(n) y(n-1) ay(n-1) a2y(n-2) y(n-2) 6

二阶数字滤波器 12 0 yn ayn ayn bxn ( ) ( 1) ( 2) ( )      x(n) b0 y(n) 12 0 yn ayn ayn bxn ( ) ( 1) ( 2) ( )   x(n) 0 b0x(n) y(n) 1 Z 1 a y n( 1)  1 Z 1 ayn( 1)  2 ayn(  2) y n( 1) 2 a 2 ayn( ) y n( 2)  6

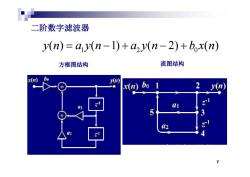
二阶数字滤波器 y(n)=ay(n-1)+ay(n-2)+box(n) 方框图结构 流图结构 r(n) x(n)bo 1 2

二阶数字滤波器 12 0 yn ayn ayn bxn yn ayn ayn bxn ( ) ( 1) ( 2) ( ) ( ) ( 1) ( 2) ( )   12 0    方框图结构 流图结构 7

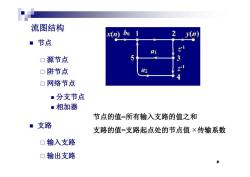
流图结构 x(n)bo 1 23(n ■节点 1 口源节点 口阱节点 42 口网络节点 ■分支节点 ■相加器 节点的值=所有输入支路的值之和 ■支路 支路的值=支路起点处的节点值×传输系数 口输入支路 口输出支路

流图结构  节点  源节点  阱节点  网络节点  分支节点  相加器  支路 节点的值=所有输入支路的值之和 支路的值 支路起点处的节点值 传输系数  输入支路 支路的值=支路起点处的节点值 传输系数  输出支路 8

8.2FIR数字滤波器的网络结构 ■直接型结构 级联型结构 ■线性相位型结构 ■频率取样型结构 ■快速卷积法

8 2 FIR 8.2 FIR数字滤波器的网络结构 数字滤波器的网络结构  直接型结构  级联型结构  线性相位型结构  频率取样型结构  快速卷积法 9

1. FIR数字滤波器的直接型结构 ■FIR数字滤波器的特点： N-1 口系统函数： H(e)=∑hn)z" 1=0 口差分方程： N y(n)= ∑hK)x(n-k) k=0 口N-1为滤波器的阶数，N为滤波器的长度 口有N-1个零点分布于z平面，z=0处是N-1阶极点 口系统的单位脉冲响应h(n)有限长，设N点 口系统函数H(z)在z>0处收敛，有限z平面只有零点，全部极 点在z=0处（因果系统) 口无输出到输入的反馈，一般为非递归型结构 10

1 FIR . FIR数字滤波器的直接型结构  FIR数字滤波器的特点：  系统函数： 1 0 () () N n n H z hnz       差分方程： 1 0 () ()( ) N k yn hk xn k       N-1为滤波器的阶数，N为滤波器的长度  有N-1个零点分布于z平面，z=0处是N-1阶极点  系统的单位脉冲响应 h(n)有限长，设N点  系统函数H(z)在 处收敛，有限z平面只有零点，全部极 点在 z = 0 处（因果系统） z  0 点在 0 处（因果系统）  无输出到输入的反馈，一般为非递归型结构 10

1. F引R数字滤波器的直接型结构（2) N- H(e)=∑n )-()x(n-) k=0 ■直接型结构（卷积型、横截型) x(n h(2 h(N-2) hN.1) ■特点： 口N-1个单位延时器，N个乘法器，N-1个加法器 口单位延时器串联，有抽头，称为延时线 11

1 FIR . FIR数字滤波器的直接型结构 数字滤波器的直接型结构（2） 1 () () N n H z hnz     1 () ()( ) N yn hk xn k      直接型结构（卷积型 横截型） 0 () () n H z hnz    0 () ()( ) k yn hk xn k    直接型结构（卷积型、横截型）  特点：  N-1个单位延时器，N个乘法器，N-1个加法器  单位延时器串联，有抽头，称为延时线 11