西安电子科技大学:《数字信号处理》课程教学课件(讲稿)09 多采样率数字信号处理

9.1引言 ■需要多采样率的场合: 口需求不同(数字电视、数字电话等) 口非平稳信号的分析 口冗余数据的存在 ■采样率转换、多采样率数字信号处理 2
9 1. 引言 需要多采样率的场合: 需求不同(数字电视、数字电话等) 非平稳信号的分析 冗余数据的存在 采样率转换 、 多采样率数字信号处理 2

采样率转换方法: ■方法一:间接转换 把离散时间信号(序列)x《n)经过D/A变换器变成模拟信 号x《t),再经AWD变换器对xt)以另一种采样率进行采样。 但经过D/A和AVD变换器都会产生量化误差,影响精度。 ■方法二:直接转换 直接在数字域对抽样信号x《)作抽样频率的变换,以得到 新的抽样信号y(m)。 x(n) y(m) F=1/T 采样率转换器 F3=1/T, 3
采样率转换方法: 方法一:间接转换 把离散时间信号(序列)x( ) n 经过D/A变换器变成模拟信 号x(t),再经A/D变换器对x(t)以另一种采样率进行采样。 但经过D/A和A/D变换器都会产生量化误差,影响精度。 方法二:直接转换 直接在数字域对抽样信号x(n)作抽样频率的变换,以得到 新的抽样信号y(m)。 采样率转换器 ( )1 x x x n F T ( ) 1 y y y m F T 3

m m 采样率转换通常分为: 采样率转换器 E=VT E=VT c抽取”(Dacimation): 高->低 c插值”(Interpolation):低->高 ■采样率转换类型 (转换前后采样率Fx和Fy的比例关系) 口整数因子抽取 F.=FD D为正整数 口整数因子插值 F,=IF 为正整数 口有理数因子采样率转换 水=% D,I互素整数 口任意因子采样率转换 水=任意有限数 4
采样率转换通常分为 采样率转换器 x( )n y m( ) 采样率转换通常分为: “抽取”(D i ti ) 高 低 采样率转换器 1 F x T x 1 F y y T “抽取”(Dacimation): 高->低 “插值”(Interpolation) 低 >高 采样率转换类型 (转换前后采样率Fx和Fy的比例关系) “插值 (Interpolation):低->高 采样率转换类型 (转换前后采样率Fx和Fy的比例关系) 整数因子抽取 F FD y x D为正整数 整数因子插值 y I F IF y x 为正整数 有理数因子采样率转换 任意因子采样率转换 , y x F I D I F D 互素整数 任意因子采样率转换 y x F F 任意有限数 4

bfLi.inbi. 20 .16 10 20 25 .i业.ii 20 -15 -10 -5 0 5 10 15 20 25 采样率转换类型? 5
采样率转换类型? 5

9.2 整数因子抽取 x(n) m 采样率转换器 F=VT E,=VT, ■问题: F,=F/D 采样率降低,导致.? 6
9 2. 整数因子抽取 x n( ) y m( ) 问题: 采样率转换器 ( ) 1 x x x n F T ( ) 1 y y y m F T 问题: 采样率降低,导致 . ? F y x F D 6

■ 原理框图 按整数因子D抽取 F,=F/D v(n) y(m)=v(Dm) D F=左 6=为% y(m)=v(Dm) n m D=2
原理框图 按整数因子D抽取 F FD y x 原理框图 按整数因子D抽取 D v n( ) y m v Dm () ( ) 1 1 F x x F T 1 x y y F F T D y m v Dm () ( ) v n( ) y( ) m D 2 7 0 n 0 m
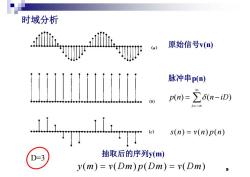
时域分析 (a) 原始信号v(n) 脉冲串p() p(n)=∑6n-iD) i=-00 TiiT s(n)=v(n)p(n) D=3 抽取后的序列y(m) y(m)=v(Dm)p(Dm)=v(Dm) 9
时域分析 原始信号v(n) 脉冲串p(n) p(n) (n iD) i p(n) (n iD) s() () () n vn pn D=3 抽取后的序列y(m) 9 D=3 y( ) y m v Dm p Dm v Dm () ( )( ) ( )

频谱关系 ■令s(n)=v(n)p(n) y(m)=s(Dm)=v(Dm)p(Dm) Y☑)=立mz“=∑sDma立s0W:n Y(Z)=>s(n)=v(p(m) DFS: =2 10
频谱关系 令 sn vn pn () () () y m s Dm v Dm p Dm () ( ) ( )( ) / ( ) ( ) ( ) () m m nD n Dm mm n Y Z y m z s Dm z s n z mm n / / ( ) () () () nD nD Y Z snz vn p n z ( ) () () () n n p 1 2 1 D j nk 0 1 : ( ) j nk D k DFS p n e D 1 2 1 / ( ) () D j nk D n D Y Z vn e z D 10 n k D 0

k=0n=-0 2)广62e v(n)台V(eo.) e)02re合e”=2rc 0,-2πk 0,=2T,0=2TxT=DT ∴0,=D0 Y(e D- D k=0 11
1 2 1 / ( ) () D j nk D n D Y Z 1 2 1 / ( ) D j nk D n D vne z / 0 ( ) () D n D n k Y Z vn e z D 0 ( ) D k n vne z D 2 2 1 1 0 1 / ( ) n j k D D k D z D vn e 1 2 0 1/ ( ) 1 j k D Dk D Ve z D D k0 n D k0 () ( ) x j vn V e 1 2 1/ 2 1 1 ( ) 1 () ( ) y y y D k j j D D j k D j Ve e D Ye Ve () ( ) 0 0 () ( ) ( ) k k Ve e D Ye Ve D y y x xy x T T T DT D ( ) 1 2 1 () ( ) y x k D D j j Y V y x D 0 11 () ( ) y D j k Y e V e D

2πk 0,=D0 2π @x-D →0,=2π 过整数因子D抽取,使数字须率区间0≤。,≤扩屉 成相应的频率区间0≤o,≤π 原采样信号频谱中o,>D 的非零频谱就会在0,=π 附近产生频谱混叠 12
2 k y x D ( ) 1 2 0 1 () ( ) y x k D D j j k Ye Ve D D k0 2 2 x y D 经过整数因子D抽取 使数字频率区间 0 扩展 经过整数因子D抽取,使数字频率区间 扩展 成相应的频率区间 0 x D 0 y 原采样信号频谱中 的非零频谱就会在 y x D y 附近产生频谱混叠 D 12
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)08 时域离散系统的实现.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)07 FIR数字滤波器(FIRDF)设计.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)06 IIR数字滤波器(IIRDF)设计.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)05 数字滤波器的基本概念及一些特殊滤波器.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)04 模拟信号数字处理.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)03 离散傅里叶变换DFT及其快速算法FFT.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)02 时域离散信号和系统的频域分析(2/2).pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)02 时域离散信号和系统的频域分析(1/2).pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)02 时域离散信号与系统 Discrete-Time Signals and Systems in the Time-Domain.pdf
- 西安电子科技大学:《数字信号处理》课程教学课件(讲稿)01 绪论(主讲:王柯俨).pdf
- 《机械工程学报》:抛物面索网天线的最佳型面设计方法(西安电子科技大学:杨东武、尤国强、保宏).pdf
- 机械电子工程中的科学计算方法(文献资料)卫星与天线相对位置 PIM CHARACTERISTICS OF THE LARGE DEPLOYABLE REFLECTOR ANTENNA MESH.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)24 总结.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)23 匹配网络设计.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)22 General Chebyshev综合.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)21 耦合谐振腔电路和耦合矩阵.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)20 交叉耦合滤波器总览.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)19 倒置变换器和微波滤波器电路.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)18 公比线带通滤波器.pdf
- 西安电子科技大学:《高等微波网络》课程教学课件(讲稿)17 半集总元件微波滤波器.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第一部分 概述 第1章 绪论(主讲:权义宁).pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第一部分 概述 第2章 网络模型.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 物理层和介质 第3章 物理层——数据和信号.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第4章 数字传输 Digital Transmission.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第5章 模拟传输 Analog Transmission.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第6章 带宽利用 Bandwidth Utilization:Multiplexing and Spreading.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第7章 传输介质.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第8章 交换.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第二部分 第9章 使用电话网和有线电视网进行数据传输.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第10章 检错与纠错 Error Detection and Correction.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第11章 数据链路控制 Data Link Control.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第12章 多路访问 Multiple Access.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第13章 有线局域网——以太网.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第14章 无线局域网.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第15章 连接局域网、主干网和虚拟局域网 Connecting LANs, Backbone Networks, and Virtual LANs.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第16章 无线WAN——移动电话和卫星网络 Cellular Telephone and Satellite Networks.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第17章 广域网SONET、SDH.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第三部分 数据链路层 第18章 虚电路网络——帧中继和ATM.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第四部分 网络层 第19章 逻辑寻址.pdf
- 西安电子科技大学:《计算机通信与网络》课程教学课件(讲稿)第四部分 网络层 第20章 IP协议.pdf
