《信号与系统》课程教学资源（实验指导）实验一 连续时间信号的MATLAB表示

信号与系统实验指导书 实验一连续时间信号的matlab表示 一、实验目的 1、熟悉典型信号的波形和特性。 2、熟悉MATLAB的运行环境，学会使用MATLAB表示连续时间信号的方法。 3、观察并熟悉典型信号的波形和特性。 二、 实验原理 从严格意义上讲，MATLAB数值计算的方法并不能处理连续时间信号。然而，可利用 连续信号在等时间间隔点的取样值来近似表示连续信号，即当取样时间间隔足够小时，这些 离散样值能够被MATLAB处理，并且能较好地近似表示连续信号。 MATLAB提供了大量生成基本信号的函数。比如常用的指数信号、正余弦信号等都是 MATLAB的内部函数。为了表示连续时间信号，需定义某一时间或自变量的范围和取样时 间间隔，然后调用该函数计算这些点的函数值，最后画出其波形图。 、指数信号f()=ke“, 若a>0,信号随时间增大而衰减： 若a<0,信号随时间增大而增大： 若α=0，信号不随时间而变化，为直流信号： 常数K表示指数信号在产0点的初始值。 越大指数信号增长或减的速越慢。 2、正弦信号f(u)=ksin(wt+) 正弦信号和余弦信号二者仅在相位上相差统称为正弦信号，其中k为振幅，W是角频率， 0为初相位。 正弦信号是周期信号，其周期T与角频率w和频率∫满足下列关系： 3、复指数信号f(0)=ke 如果指数信号的指数因子为一复数，则称之为复指数信号，其中s=σ+N为复数。借 助欧拉公式展开，可得ke”=keo+m"=ke”cos(wl)+kesin(wD） 此结果表明 一个复指数信号可分解为实、虚两部分。其中，实部包含余弦信号，虚部 则为正弦信号。指数因子实部表征了正弦与余弦函数振幅随时间变化的情况。指数因子的 -1-

信号与系统实验指导书 -1- 实验一 连续时间信号的 matlab 表示 一、 实验目的 1、 熟悉典型信号的波形和特性。 2、 熟悉 MATLAB 的运行环境，学会使用 MATLAB 表示连续时间信号的方法。 3、 观察并熟悉典型信号的波形和特性。 二、 实验原理 从严格意义上讲，MATLAB 数值计算的方法并不能处理连续时间信号。然而，可利用 连续信号在等时间间隔点的取样值来近似表示连续信号，即当取样时间间隔足够小时，这些 离散样值能够被 MATLAB 处理，并且能较好地近似表示连续信号。 MATLAB 提供了大量生成基本信号的函数。比如常用的指数信号、正余弦信号等都是 MATLAB 的内部函数。为了表示连续时间信号，需定义某一时间或自变量的范围和取样时 间间隔，然后调用该函数计算这些点的函数值，最后画出其波形图。 1、指数信号 at f t ke ( )  ， 若 a  0 ，信号随时间增大而衰减； 若 a  0 ，信号随时间增大而增大； 若 a  0 ，信号不随时间而变化，为直流信号； 常数 K 表示指数信号在产 0 点的初始值。 a 1   ， 越大，指数信号增长或衰减的速率越慢。 2、 正弦信号 f (t)  k sin(wt ) 正弦信号和余弦信号二者仅在相位上相差统称为正弦信号，其中 k 为振幅， w 是角频率，  为初相位。 正弦信号是周期信号，其周期 T 与角频率 w 和频率 f 满足下列关系： w f T 2 1    3、复指数信号 st f t ke ( )  如果指数信号的指数因子为一复数，则称之为复指数信号，其中 s   jw 为复数。借 助欧拉公式展开，可得 cos( ) sin( ) ( ) ke ke ke wt jke wt st  jw t t t      此结果表明，一个复指数信号可分解为实、虚两部分。其中，实部包含余弦信号，虚部 则为正弦信号。指数因子实部 d 表征了正弦与余弦函数振幅随时间变化的情况。指数因子的

信号与系统实验指导书 虚部w则表示正弦与余弦信号的角频率。 若σ>0，正弦、余弦信号是增幅振荡： 若。>0，正弦及余弦信号是衰减振荡： 若σ=0，即s为虚数，则正弦、余弦信号是等幅振荡： 若=0，即s为实数，则复指数信号成为一般的指数信号 若σ=0，=0，即s等于零，则复指数信号的实部和虚部都与时间无关，成为直流 信号。 虽然实际上不能产生复指数信号，但是它概括了多种情况，可以利用复指数信号来描述 各种基本信号，如直流信号、指数信号、正弦或余弦信号以及增长或衰减的正弦与余弦信号。 利用复指数信号可使许多运算和分析得以简化。 4、抽样信号a0=sn Sa()信号是一个偶函数，t=土π，2π，士nπ时，函数值等于零，在1的正、负两 方向振幅都逐渐衰减。 5、单位斜变信号f)=tu() 斜变信号也称斜坡信号或斜升信号，指从某一时刻开始随时间正比例增长的信号。如果 增长的变化率是1，就称作单位斜变信号 6、单位阶跃信号u() u(t) (0)一般无定义，通常认为在1=0瞬间信号值从0跳变到1，有时为分析问愿方便在 某些情况下也定义u(O)=号 阶跃信号具有较强的单边特性。即信号在接入时刻以前幅度为0。 7、矩形脉冲信号R()=(-(1-T) 为书写方便，常利用阶跃信号及其延时信号之差来表示矩形脉冲，其中下标T表示矩形 脉冲出现在0到T时刻之间。 8、单位冲微信号 0=+空-u- Tsodr=1 6(t)=0(t≠0)

信号与系统实验指导书 -2- 虚部 w 则表示正弦与余弦信号的角频率。 若   0 ，正弦、余弦信号是增幅振荡； 若   0 ，正弦及余弦信号是衰减振荡； 若   0 ，即 s 为虚数，则正弦、余弦信号是等幅振荡； 若 w  0 ，即 s 为实数，则复指数信号成为一般的指数信号； 若   0 ， w  0 ，即 s 等于零，则复指数信号的实部和虚部都与时间无关，成为直流 信号。 虽然实际上不能产生复指数信号，但是它概括了多种情况，可以利用复指数信号来描述 各种基本信号，如直流信号、指数信号、正弦或余弦信号以及增长或衰减的正弦与余弦信号。 利用复指数信号可使许多运算和分析得以简化。 4、抽样信号 t t Sa t sin( ) ( )  Sa(t) 信号是一个偶函数， t  ,2,.,n 时，函数值等于零，在 t 的正、负两 方向振幅都逐渐衰减。 5、单位斜变信号 f (t)  tu(t) 斜变信号也称斜坡信号或斜升信号，指从某一时刻开始随时间正比例增长的信号。如果 增长的变化率是 1，就称作单位斜变信号 6、单位阶跃信号 u(t) u(0) 一般无定义，通常认为在 t  0 瞬间信号值从 0 跳变到 1，有时为分析问题方便在 某些情况下也定义 2 1 u(0)  。 阶跃信号具有较强的单边特性。即信号在接入时刻以前幅度为 0。 7、矩形脉冲信号 R (t) u(t) u(t T) T    为书写方便，常利用阶跃信号及其延时信号之差来表示矩形脉冲，其中下标 T 表示矩形 脉冲出现在 0 到 T 时刻之间。 8、单位冲激信号                 ( ) 0 ( 0) ( ) 1 )] 2 ) ( 2 [ ( 1 ( ) lim 0 t t t dt t u t u t       

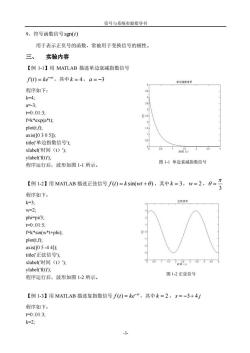
信号与系统实验指导书 9、符号函数信号sg(t) 用于表示正负号的函数，常被用于变换信号的极性。 三、实验内容 【例I-I】用MATLAB描述单边衰减指数信号 f0)=kem,其中k=4,a=-3 单达拥数信号 程序如下： k=4 a=.3: 133 =0.01:3 f-k*exp(a*t); plot(tf): axis([0305]). tile(单边指数信号)， 0 xlabel'(时间(t))方 05 时。22西 ylabel(f(tY): 程序运行后，波形如图11所示。 图11单边衰减指数信号 【例121用MAB指达正弦信号f0=ks1+),共中k=3,W=2,g-骨 程序如下： k=3: w=2: phi-pi/3. =0:.01:5: f=k*sin(w*t+phi) plot(t,f); axis([0 5-441): title(正弦信号)； xlabel('时间(t)) ylabel('f(t)); 图12正弦信号 程序运行后，波形如图1-2所示。 【例1-3】用MATLAB描述复指数信号f)=ke,其中k=2,S=-3+4j 程序如下： t001:3: k=2: 3

信号与系统实验指导书 -3- 9、符号函数信号 sgn(t) 用于表示正负号的函数，常被用于变换信号的极性。 三、 实验内容 【例 1-1】用 MATLAB 描述单边衰减指数信号 at f t ke ( )  ，其中 k  4，a  3 程序如下： k=4; a=-3; t=0:.01:3; f=k*exp(a*t); plot(t,f); axis([0 3 0 5]); title('单边指数信号'); xlabel('时间（t）'); ylabel('f(t)'); 程序运行后，波形如图 1-1 所示。 【例 1-2】用 MATLAB 描述正弦信号 f (t)  k sin(wt ) ，其中 k  3， w  2 ， 3    程序如下： k=3; w=2; phi=pi/3; t=0:.01:5; f=k*sin(w*t+phi); plot(t,f); axis([0 5 -4 4]); title('正弦信号'); xlabel('时间（t）'); ylabel('f(t)'); 程序运行后，波形如图 1-2 所示。 【例 1-3】用 MATLAB 描述复指数信号 st f t ke ( )  ，其中 k  2 ， s  3 4 j 程序如下： t=0:.01:3; k=2; 图 1-1 单边衰减指数信号 图 1-2 正弦信号

信号与系统实验指导书 a=3 b=4: f-k*exp((a+b*i)*t) subplot(2,2,1): plot(t,rcal(D)).title(实部)，xlabel(时间(t)方 subplot(2.2.2): plot(t,.imag(,tite('虚部)，xlabel(r时间(t) subplot(2.2.3): plot(,tabs(D).tite((模)，xlabel(r时间(t)方 subplot(2.2.4): plot(t.angIe(),e(相角'):xlabel(r时间(t) 程序运行后，波形如图1-3所示。 实部 虚部 05 050 时间() 相角 4 05 2 06 时间() 时间(t) 图1-3复指数信号 【例1-4】用MATLAB描述单位斜变信号u()。 程序如下： t0.013: k=2: f=k*t plot(t,f); tile(斜变信号)

信号与系统实验指导书 -4- a=-3 b=4; f=k*exp((a+b*i)*t); subplot(2,2,1); plot(t,real(f));title('实部');xlabel('时间（t）'); subplot(2,2,2); plot(t,imag(f));title('虚部');xlabel('时间（t）'); subplot(2,2,3); plot(t,abs(f));title('模');xlabel('时间（t）'); subplot(2,2,4); plot(t,angle(f));title('相角');xlabel('时间（t）'); 程序运行后，波形如图 1-3 所示。 【例 1-4】用 MATLAB 描述单位斜变信号 tu(t)。 程序如下： t=0:.01:3; k=2; f=k*t; plot(t,f); title('斜变信号'); 图 1-3 复指数信号 图 1-3 复指数信号

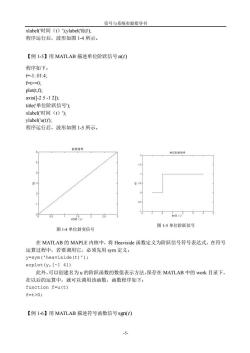
信号与系统实验指导书 xlabel'(时间(t))ylabel('f(t')): 程序运行后，波形如图14所示 【例1-5】用MATLAB描述单位阶跃信号() 程序如下： t=1:.014 f-t>-0; plot(t,f); axis-25-12 title(单位阶跃信号)： xlabel('时间(t) ylabel('u(t)); 程序运行后，波形如图1-5所示 变信号 单收翰跃信号 1 图14单位斜变信号 图1-5单位阶跃信号 在MATLAB的MAPLE内核中，将Heaviside函数定义为阶跃信号符号表达式，在符号 运算过程中，若要调用它，必须先用sym定义： y=sym('heaviside(t)'); ezp1ot(y,[-14]) 此外，可以创建名为u的阶跃函数的数值表示方法，保存在MATLAB中的wok目录下， 在以后的运算中，就可以调用该函数，函数程序如下： function f=u(t) f=t>0: 【例1-6】用MATLAB描述符号函数信号sgn(t)

信号与系统实验指导书 -5- xlabel('时间（t）');ylabel('f(t)'); 程序运行后，波形如图 1-4 所示。 【例 1-5】用 MATLAB 描述单位阶跃信号 u(t) 程序如下： t=-1:.01:4; f=t>=0; plot(t,f); axis([-2 5 -1 2]); title('单位阶跃信号'); xlabel('时间（t）'); ylabel('u(t)'); 程序运行后，波形如图 1-5 所示。 在 MATLAB 的 MAPLE 内核中，将 Heaviside 函数定义为阶跃信号符号表达式，在符号 运算过程中，若要调用它，必须先用 sym 定义： y=sym('heaviside(t)'); ezplot(y,[-1 4]) 此外，可以创建名为 u 的阶跃函数的数值表示方法，保存在 MATLAB 中的 work 目录下， 在以后的运算中，就可以调用该函数，函数程序如下： function f=u(t) f=t>0; 【例 1-6】用 MATLAB 描述符号函数信号 sgn(t) 图 1-4 单位斜变信号 图 1-5 单位阶跃信号

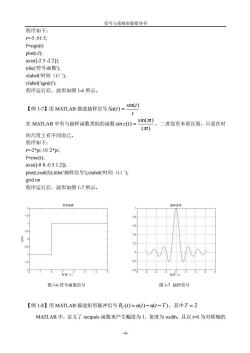
信号与系统实验指导书 程序如下： t=-5.01:5: f-sign(t) plot(t,f); axis[-25-22 title(符号函数)， xlabel(时间(t) ylabel('sgn(t)); 程序运行后，波形如图1-6所示 【例1-7】用MATLAB描述抽样信号Sa0=sin 在MATLAB中有与抽样函数类似的函数sinc0=Sim ，二者没有本质区别，只是在时 (m) 间尺度上有不同而己。 程序如下： t=-2pi:.01:2*pi f=sinc(t), axis(-88-0.51.2 plot(treal(f),tie(抽样信号)，xlabel(时间(t)), grid on 程序运行后，波形如图1-7所示。 游号运策 图16符号函数信号 图17抽样信号 【例1-8】用MATLAB描述矩形脉冲信号R,()=(t)-(t-T),其中T=2 MATLAB中，定义了rectpuls函数来产生幅度为l,宽度为width,且以O为对称轴的

信号与系统实验指导书 -6- 程序如下： t=-5:.01:5; f=sign(t) plot(t,f); axis([-2 5 -2 2]); title('符号函数'); xlabel('时间（t）'); ylabel('sgn(t)'); 程序运行后，波形如图 1-6 所示。 【例 1-7】用 MATLAB 描述抽样信号 t t Sa t sin( ) ( )  在 MATLAB 中有与抽样函数类似的函数 ( ) sin( ) sin ( ) t t c t    ，二者没有本质区别，只是在时 间尺度上有不同而已。 程序如下： t=-2*pi:.01:2*pi; f=sinc(t); axis([-8 8 -0.5 1.2]); plot(t,real(f));title('抽样信号');xlabel('时间（t）'); grid on 程序运行后，波形如图 1-7 所示。 【例 1-8】用 MATLAB 描述矩形脉冲信号 R (t) u(t) u(t T) T    ，其中 T  2 MATLAB 中，定义了 rectpuls 函数来产生幅度为 1，宽度为 width，且以 t=0 为对称轴的 图 1-6 符号函数信号 图 1-7 抽样信号

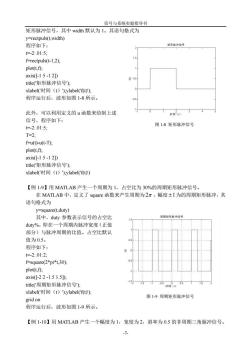
信号与系统实验指导书 矩形脉冲信号，其中widh默认为1。其语句格式为 y=rectpuls(t,width) 程序如下： 师无冲情可 te2015 f白rectpuls(t-l,2: plot(tf); axis(-15-12 e(矩形脉冲信号)方 xlabel(时间(t))ylabel('f(t): 程序运行后，波形如图1-8所示 此外，可以利用定义的山函数来绘制上述 时世， 信号，程序如下： t=-2.01:5 图1-8矩形脉冲信号 T=2: =u)-u(t-T方 plot(t,f); axis([-1 5-1 21) tile矩形脉冲信号， xlabel(时间(t))ylabel(f) 【例1-9】用MATLAB产生一个周期为1，占空比为30%的周期矩形脉冲信号。 在MATLAB中，定义了square函数来产生周期为2π，幅度±1为的周期矩形脉冲，其 语句格式为 v=square(tduty) 其中，duy参数表示信号的占空比 商期矩市感冲信号 duy%,即在一个周期内脉冲宽度（正值 部分)与脉冲周期的比值。占空比默认 值为0.5。 程序如下： =-2:.01:2 f-square(2*pi*t.30): plot(t,f): axis[-22-1515 title(周期矩形脉冲信号)， xlabel'(时间(t)ylabel('f(t)) grid on 图19周期矩形脉冲信号 程序运行后，波形如图19所示 【例1-10】用MATLAB产生一个幅度为1，宽度为2，斜率为0.5的非周期三角脉冲信号

信号与系统实验指导书 -7- 矩形脉冲信号，其中 width 默认为 1。其语句格式为 y=rectpuls(t,width) 程序如下： t=-2:.01:5; f=rectpuls(t-1,2); plot(t,f); axis([-1 5 -1 2]) title('矩形脉冲信号'); xlabel('时间（t）');ylabel('f(t)'); 程序运行后，波形如图 1-8 所示。 此外，可以利用定义的 u 函数来绘制上述 信号，程序如下： t=-2:.01:5; T=2; f=u(t)-u(t-T); plot(t,f); axis([-1 5 -1 2]) title('矩形脉冲信号'); xlabel('时间（t）');ylabel('f(t)') 【例 1-9】用 MATLAB 产生一个周期为 1，占空比为 30%的周期矩形脉冲信号。 在 MATLAB 中，定义了 square 函数来产生周期为 2 ，幅度 1 为的周期矩形脉冲，其 语句格式为 y=square(t,duty) 其中，duty 参数表示信号的占空比 duty%，即在一个周期内脉冲宽度（正值 部分）与脉冲周期的比值。占空比默认 值为 0.5。 程序如下： t=-2:.01:2; f=square(2*pi*t,30); plot(t,f); axis([-2 2 -1.5 1.5]); title('周期矩形脉冲信号'); xlabel('时间（t）');ylabel('f(t)'); grid on 程序运行后，波形如图 1-9 所示。 【例 1-10】用 MATLAB 产生一个幅度为 1，宽度为 2，斜率为 0.5 的非周期三角脉冲信号。 图 1-8 矩形脉冲信号 图 1-9 周期矩形脉冲信号

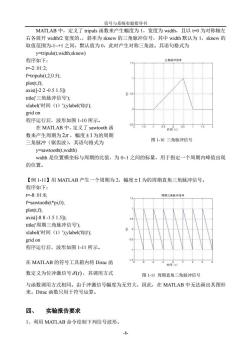
信号与系统实验指导书 MATLAB中，定义了tripuls函数来产生幅度为l,宽度为widh,且以0为对称轴左 右各展开width/2宽度的、，斜率为sknew的三角脉冲信号，其中width默认为l,sknew的 取值范围为1+1之间，默认值为0，此时产生对称三角波。其语句格式为 y=tripuls(t,width,sknew) 程序如下 三角航冲信号 =-2:.01:2: f-tripuls(t.2.0.5): plot(t,f); axis(-22-0.51.5]） title(三角脉冲信号， xlabel(时间(t)):ylabel('f(t)) grid on 程序运行后，波形如图1-10所示。 在MATLAB中，定义了sawtooth函 an间o 数来产生周期为2π，幅度±1为的周期 三角脉冲（锯齿波），其语句格式为 图1-10三角脉冲信号 y-sawtooth(t,width) widh是位置横坐标与周期的比值，为0~1之间的标量，用于指定一个周期内峰值出现 的位置。 【例1-11】用MATLAB产生一个周期为2，幅度±1为的周期直角三角脉冲信号。 程序如下： t=-8:.018: 期三角酸冲信 f=sawtooth(t*pi,0); plot(t,f): axis-88-1.51.5J title(周期三角脉冲信号)： xlabel'(时间(t)ylabel('f(t))方 grid on 程序运行后，波形如图1-11所示。 在MATLAB的符号工具箱内将Dirac函 15 数定义为位冲激信号δ)，其调用方式 图111周期直角三角脉冲信号 与函数调用方式相同。由于冲激信号幅度为无穷大，因此，在MATLAB中无法画出其图形 来。Dirac函数只用于符号运算。 四、实验报告要求 I、利用MATLAB命令绘制下列信号波形

信号与系统实验指导书 -8- MATLAB 中，定义了 tripuls 函数来产生幅度为 1，宽度为 width，且以 t=0 为对称轴左 右各展开 width/2 宽度的、，斜率为 sknew 的三角脉冲信号，其中 width 默认为 1，sknew 的 取值范围为-1~+1 之间，默认值为 0，此时产生对称三角波。其语句格式为 y=tripuls(t,width,sknew) 程序如下： t=-2:.01:2; f=tripuls(t,2,0.5); plot(t,f); axis([-2 2 -0.5 1.5]) title('三角脉冲信号'); xlabel('时间（t）');ylabel('f(t)'); grid on 程序运行后，波形如图 1-10 所示。 在 MATLAB 中，定义了 sawtooth 函 数来产生周期为 2 ，幅度 1 为的周期 三角脉冲（锯齿波），其语句格式为 y=sawtooth(t,width) width 是位置横坐标与周期的比值，为 0~1 之间的标量，用于指定一个周期内峰值出现 的位置。 【例 1-11】用 MATLAB 产生一个周期为 2，幅度 1 为的周期直角三角脉冲信号。 程序如下： t=-8:.01:8; f=sawtooth(t*pi,0); plot(t,f); axis([-8 8 -1.5 1.5]); title('周期三角脉冲信号'); xlabel('时间（t）');ylabel('f(t)'); grid on 程序运行后，波形如图 1-11 所示。 在 MATLAB 的符号工具箱内将 Dirac 函 数定义为位冲激信号  (t) ，其调用方式 与函数调用方式相同。由于冲激信号幅度为无穷大，因此，在 MATLAB 中无法画出其图形 来。Dirac 函数只用于符号运算。 四、 实验报告要求 1、利用 MATLAB 命令绘制下列信号波形。 图 1-10 三角脉冲信号 图 1-11 周期直角三角脉冲信号

信号与系统实验指导书 (D3sin21+7 (2)ecos(10m)t-)-t-2] (3)(2-e')ut) 2、利用MATLAB命令绘制下列复信号的实部、虚部、模和相角。 (1)( 2f0=e+e月

信号与系统实验指导书 -9- （1） ) 3 3sin(2  t  （2） cos(10 ) ( 1)  (  2)  e t u t u t t  （3） (2 e )u(t) t  （4） sin( ) sin(8 ) 2 1 1 wt wt        2、利用 MATLAB 命令绘制下列复信号的实部、虚部、模和相角。 （1） j t f t e 2) 5 ( ( )    （2） j t j t f t e e 3 2 ( )     图 1-6 符号 函数信号