《信号与系统》课程教学资源（实验指导）实验五 周期信号的合成与分解

信号与系统实验指导书 实验五周期信号的分解与合成 一、实验目的 1、熟悉信号的合成、分解原理，加深对傅里叶级数的理解。 2、了解和认识吉布斯现象(Gibbs)。 3、学会使用MATLAB分析傅立叶级数展开。 二、实验原理 根据周期信号的傅里叶级数展开式可知，任何非正弦周期信号，只要满足狄利克雷条件， 都可以分解为三角形式的傅立叶级数，即一直流分量和由基波及各次谐波（基波的整数倍） 分量的叠加，这些正弦、余弦分量的频率必定是基频W,的整数倍。通常把频率？，称为基波， 频率为2州，、3.等分量分别称为二次谐波、三次谐波.。显然，直流分量的大小以及基 波与各次谐波的幅度、相位取决于周期信号的波形。 f)=a。+∑[a cos(mw,)+bsin(mw,t 其中： 直流分量：a= 余孩分量的度：a,-0ema 正弦分量的度：6.=0smh 此外，任何满足满足狄利克雷条件的周期信号，也可以分解为指数形式的傅立叶级数 f)=∑F(mw,)em 其中： F(m)r 合成波形所包含的谐波分量愈多，除间断点附近外，它愈接近于原方波信号，在间断点

信号与系统实验指导书 -1- 实验五 周期信号的分解与合成 一、实验目的 1、熟悉信号的合成、分解原理，加深对傅里叶级数的理解。 2、了解和认识吉布斯现象(Gibbs)。 3、学会使用 MATLAB 分析傅立叶级数展开。 二、实验原理 根据周期信号的傅里叶级数展开式可知，任何非正弦周期信号，只要满足狄利克雷条件， 都可以分解为三角形式的傅立叶级数，即一直流分量和由基波及各次谐波（基波的整数倍） 分量的叠加，这些正弦、余弦分量的频率必定是基频 w1 的整数倍。通常把频率 w1 称为基波， 频率为 2w1 、3w1 .等分量分别称为二次谐波、三次谐波.。显然，直流分量的大小以及基 波与各次谐波的幅度、相位取决于周期信号的波形。        1 0 1 1 ( ) cos( ) sin( ) n n n f t a a nw t b nw t 其中： 直流分量：    0 1 0 ( ) 1 1 0 t T t f t dt T a 余弦分量的幅度：    0 1 0 ( )cos( ) 1 1 1 t T t n f t nw t dt T a 正弦分量的幅度：    0 1 0 ( )sin( ) 1 1 1 t T t n f t nw t dt T b 此外，任何满足满足狄利克雷条件的周期信号，也可以分解为指数形式的傅立叶级数。      n jnwt f t F nw e 1 ( ) ( )1 其中：     0 1 0 1 ( ) 1 ( ) 1 1 t T t jnwt f t e dt T F nw 合成波形所包含的谐波分量愈多，除间断点附近外，它愈接近于原方波信号，在间断点

信号与系统实验指导书 附近，随着所含谐波次数的增高，合成波形的尖峰愈靠近间断点，但尖峰幅度并未明显减小， 可以正明，即使合成波形所含谐波次数n→∞时，在间断点附近仍有约9%的偏差，这种现 象称为吉布斯现象(Gibbs)。 三、实验内容 【例5-1】已知周期矩形脉冲信号的傅立叶级数为： π 其中，E=1,T=1请编程实现其各次谐波的叠加。 程序如下： close all e-1.001:1 w=2+pi; y=square(2*pi*t.50) plot(ty); gridon xlabel('t: ylabel(周期方波信号) axis-11-l.51.5J nmax-[1351147 N=length(n_max). for k=1:N n=1:2:n max(k): x=(4./(pi*n))*sin(w*n'*t): figure; plot(L.y): hold on: plot(t.x): hold off: xlabel(t): ylabel(部分和的波形 axis-l1-1.51.5] grid on title(『最大谐波数=，num2str(_maxk) end 程序运行后，波形如图51所示

信号与系统实验指导书 -2- 附近，随着所含谐波次数的增高，合成波形的尖峰愈靠近间断点，但尖峰幅度并未明显减小， 可以证明，即使合成波形所含谐波次数 n  时，在间断点附近仍有约 9%的偏差，这种现 象称为吉布斯现象(Gibbs)。 三、实验内容 【例 5-1】已知周期矩形脉冲信号的傅立叶级数为： sin(7 )) 7 1 sin(5 ) 5 1 sin(3 ) 3 1 (sin( ) 4 ( ) 1 1 1 1 w t w t w t w t E f t      其中，E=1，T=1 请编程实现其各次谐波的叠加。 程序如下： close all t=-1:.001:1; w=2*pi; y=square(2*pi*t,50); plot(t,y); grid on xlabel('t'); ylabel('周期方波信号'); axis([-1 1 -1.5 1.5]); n_max=[ 1 3 5 11 47]; N=length(n_max); for k=1:N n=1:2:n_max(k); x=(4./(pi*n))*sin(w*n'*t); figure; plot(t,y); hold on ; plot(t,x); hold off; xlabel('t'); ylabel('部分和的波形'); axis([-1 1 -1.5 1.5]); grid on title(['最大谐波数=',num2str(n_max(k))]) end 程序运行后，波形如图 5-1 所示

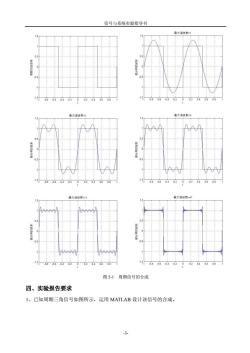
信号与系统实验指导书 最大增一 06040.2 02.040608 15006040立040 0664D2 0204050 图51周期信号的合成 四、实验报告要求 1、已知周期三角信号如图所示，运用MATLAB设计该信号的合成

信号与系统实验指导书 -3- 图 5-1 周期信号的合成 四、实验报告要求 1、已知周期三角信号如图所示，运用 MATLAB 设计该信号的合成

信号与系统实验指导书 ↑r() -1 0 1 图5-2周期三角信号 2、已知周期全波余弦信号的傅立叶级数如下，试用MTALAB实现3次、5次、9次和25 次谐波的合成波形。 f0=2E+45,1 1 -15o20+357os3wp0+J -2E+4E (4n-1 cos(2mt)

信号与系统实验指导书 -4- 2、已知周期全波余弦信号的傅立叶级数如下，试用 MTALAB 实现 3 次、5 次、9 次和 25 次谐波的合成波形。 cos(2 ) (4 1) 1 ( 1) 2 4 cos(3 ) .] 35 1 cos(2 ) 15 1 cos( ) 3 1 [ 2 4 ( ) 0 1 2 1 1 1 1 nw t n E E wt wt wt E E f t n n                   图 5-2 周期三角信号 图 1-6 符号 函数信号