《结构力学》课程教学资源（习题解答）第十二章 矩阵位移法

第十二章矩阵位移法 一、基本概念 矩阵位移法，又称之为杆系结构的有限元法。有限元法解题思路分两大步，一是单元 分析，即写出单元杆端力和杆端位移的关系矩阵，也称单元刚度方程：二是整体分析，即利 用平衡条件写出结构的刚度方程，它表示结点荷载和结点位移的关系矩阵。由整体分析求结 点位移，将求得的结点位移带入单元刚度方程求杆端力，这就是矩阵位移法的总体思路。 二、部分题解 12-1（a)试用先处理法建立图示各连续梁的结构刚度矩阵。设E=常量。 1 k上 k上以 解(1)结点编号、单元编号如图 (2)单元定位向量 {ay"=[0102 {242=[0203 {2=[0304 (3)单元刚度矩阵 「12EI 6EI 奖 _12EL 了曲了 迎地了 引入边界条件并换码： k 1

第十二章 矩阵位移法 一、基本概念 矩阵位移法，又称之为杆系结构的有限元法。有限元法解题思路分两大步，一是单元 分析，即写出单元杆端力和杆端位移的关系矩阵，也称单元刚度方程；二是整体分析，即利 用平衡条件写出结构的刚度方程，它表示结点荷载和结点位移的关系矩阵。由整体分析求结 点位移，将求得的结点位移带入单元刚度方程求杆端力，这就是矩阵位移法的总体思路。 二、部分题解 12-1（a）试用先处理法建立图示各连续梁的结构刚度矩阵。设 EI=常量。 解 （1）结点编号、单元编号如图 （2）单元定位向量     (1) 0 1 0 2 T  =     (2) 0 2 0 3 T  =     (3) 0 3 0 4 T  = （3）单元刚度矩阵 (1) 3 2 3 2 (1) 2 2 (1) 11 12 21 22 3 2 3 2 2 2 12 6 12 6 6 4 6 2 12 6 12 6 6 2 6 4 EI EI EI EI l l l l EI EI EI EI k k l l l l k k k EI EI EI EI l l l l EI EI EI EI l l l l   −       −     = =         − − −       −     引入边界条件并换码： (1) (1) (1) 11 12 21 22 4 2 2 4 EI EI k k l l k k k EI EI l l       = =            

使 只 9 引入边界条件并换码： 12 I: P N m- F场L 1 引入边界条件并换码： [「4E 2E17 2 (4)结构的刚度矩阵 k, 7 「420 0 k) [K]= 0 EI261 016 2 10 0 0024 若是后处理法，要有单元刚度矩阵子块对号入座，形成结构的原始刚度矩阵[K]

(2) 3 2 3 2 (2) 2 2 (2) 22 23 32 33 3 2 3 2 2 2 3 3 3 3 2 2 2 3 2 3 2 3 3 3 3 2 2 2 2 3 3 2 2 2 EI EI EI EI l l l l EI EI EI EI k k l l l l k k k EI EI EI EI l l l l EI EI EI EI l l l l   −       −     = =         − − −       −     引入边界条件并换码： (2) (2) (2) 22 23 32 33 2 2 EI EI k k l l k k k EI EI l l       = =             (1) 3 2 3 2 (3) 2 2 (3) 33 34 43 44 3 2 3 2 2 2 12 6 12 6 6 4 6 2 12 6 12 6 6 2 6 4 EI EI EI EI l l l l EI EI EI EI k k l l l l k k k EI EI EI EI l l l l EI EI EI EI l l l l   −       −     = =         − − −       −     引入边界条件并换码： (3) (3) (3) 33 34 43 44 4 2 2 4 EI EI k k l l k k k EI EI l l       = =             （4）结构的刚度矩阵   (1) (1) 11 12 (1) (1) (2) (2) 21 22 23 (2) (2) (3) (3) 32 33 34 (3) (3) 43 44 0 0 4 2 0 0 0 2 6 1 0 0 0 1 6 2 0 0 0 0 2 4 k k k k k EI K k k k l k k + +         = =                   若是后处理法，要有单元刚度矩阵子块对号入座，形成结构的原始刚度矩阵 K0 

[k9[k"⊥0⊥0 k1aP。 [k2 [k3][k] 00[k]9[k] 再引入边界条件，将零位移对应的行和列删除，即得到结构刚度矩阵K】 12-1(b)试用先处理法建立图示各连续梁的结构刚度矩阵。设E常量。 解(1)结点编号、单元编号、结点位移编号如图 会&金 (2)单元定位向量 {2"=[000 {22=[0123 {2}-[2304 {a)-[0456 (3)单元刚度矩阵 单元(1)：{"=[000 「24E1 12EI: 1 2 L- 12EI I; 出 1 1 引入边界条件并换码： e-r- 单元2：-[0123

                      (1) (1) 11 12 (1) (1) (2) (2) 21 22 23 0 (2) (2) (3) (3) 32 33 34 (3) (3) 43 44 0 0 0 0 0 0 k k k k k K k k k k k + +       =           再引入边界条件，将零位移对应的行和列删除，即得到结构刚度矩阵 K  12-1（b）试用先处理法建立图示各连续梁的结构刚度矩阵。设 EI=常量。 解 （1）结点编号、单元编号、结点位移编号如图 （2）单元定位向量     (1) 0 0 0 1 T  =     (2) 0 1 2 3 T  =     (3) 2 3 0 4 T  =     (4) 0 4 5 6 T  = （3）单元刚度矩阵 单元（1）：     (1) 0 0 0 1 T  = (1) 3 2 3 2 (1) 2 2 (1) 11 12 21 22 3 2 3 2 2 2 24 12 24 12 12 8 12 4 24 12 24 12 12 4 12 8 EI EI EI EI l l l l EI EI EI EI k k l l l l k k k EI EI EI EI l l l l EI EI EI EI l l l l   −       −     = =         − − −       −     引入边界条件并换码：   (1) (1) (1) 11 8EI k k l   = =     单元（2）：     (2) 0 1 2 3 T  =

题人 0 12EI 1 引入边界条件并换码： 8EI 72 k2=k 12ET 2 单元(3：{2}=[2 30 4 12EI 黑 下 引入边界条件并换码 下 兽 单元(4)2}=[0 456

(2) 3 2 3 2 (2) 2 2 (2) 22 23 32 33 3 2 3 2 2 2 24 12 24 12 12 8 12 4 24 12 24 12 12 4 12 8 EI EI EI EI l l l l EI EI EI EI k k l l l l k k k EI EI EI EI l l l l EI EI EI EI l l l l   −       −     = =         − − −       −     引入边界条件并换码： (2) 2 (2) 11 12 13 (2) 21 22 23 2 3 2 31 32 33 2 8 12 4 12 24 12 4 12 8 EI EI EI l l l k k k EI EI EI k k k k l l l k k k EI EI EI l l l   −           = = − −             −     单元（3）：     (3) 2 3 0 4 T  = (1) 3 2 3 2 (3) 2 2 (3) 33 34 43 44 3 2 3 2 2 2 12 6 12 6 6 4 6 2 12 6 12 6 6 2 6 4 EI EI EI EI l l l l EI EI EI EI k k l l l l k k k EI EI EI EI l l l l EI EI EI EI l l l l   −       −     = =         − − −       −     引入边界条件并换码： (3) 3 2 2 (3) 22 23 24 (3) 32 33 34 2 42 43 44 2 12 6 6 6 4 2 6 2 4 EI EI EI l l l k k k EI EI EI k k k k l l l k k k EI EI EI l l l             = =                 单元（4）     (4) 0 4 5 6 T  =

0 2 引入边界条件并换码： 4EI [ka e 6EI (4)结构的刚度矩阵 「kH2 0 0 0 [K]= k 0 0 0 0 0 0 专 6 4 0 0 0 碧 0 0 4 0 0 0 n -9 2 0 0 - 0 0 0 2 4 12一8试用先处理法计算图示平面刚架（忽略周向变形），并作其弯矩图。E=常量 解(1)建立坐标，结点编号、单元编号、结点位移编号如图

(4) 3 2 3 2 (4) 2 2 (4) 44 45 54 55 3 2 3 2 2 2 12 6 12 6 6 4 6 2 12 6 12 6 6 2 6 4 EI EI EI EI l l l l EI EI EI EI k k l l l l k k k EI EI EI EI l l l l EI EI EI EI l l l l   −       −     = =         − − −       −     引入边界条件并换码： (4) 2 (4) 44 45 46 (4) 54 55 56 2 3 2 64 65 66 2 4 6 2 6 12 6 2 6 4 EI EI EI l l l k k k EI EI EI k k k k l l l k k k EI EI EI l l l   −           = = − −             −     （4）结构的刚度矩阵   (1) (2) (2) (2) 11 12 13 (2) (2) (3) (2) (3) (3) 21 22 23 24 (2) (2) (3) (2) (3) (3) 31 32 33 34 (3) (3) (3) (4) (4) (3) 42 43 44 45 46 (4) (4) (4) 54 55 56 (4) (4) (4) 64 65 66 0 0 0 0 0 0 0 0 0 0 0 0 0 0 k k k k k k k k k k k K k k k k k k k k k k k + + + + + +     =   2 2 12 16 4 0 0 0 12 36 6 6 0 0 6 4 12 2 0 0 6 6 0 2 8 2 6 12 6 0 0 0 6 0 0 0 2 4 l l l l l EI l l l l l l l l   −   − − − = − − − −   12—8 试用先处理法计算图示平面刚架（忽略周向变形），并作其弯矩图。EI=常量 解 （1）建立坐标，结点编号、单元编号、结点位移编号如图

4444 (b)图结点位移 单元 单元定位向量 1-2 {4}=[0102 (2) 2→3 {2}=0203 (3) 4-3 {4}=[0003 (4) 3→5 {8}=0300] 结点位移列阵 {△}=[A△2△ (2)单元刚度矩阵 单元(1)：{}"=[000 「12E1 6EI. 12E1 6EI 3 13 _6EI k0= 1.2 1. 12 12E 1 6EI 2EI 6EI 1 引入边界条件并换码： 1 1 单元(2)：{}2=[0203

单元 i → j 单元定位向量 (1) 1→2  1 [0102]T  = (2) 2→3  2 [0203]T  = (3) 4→3  3 [0003]T  = (4) 3→5  4 [0300]T  = 结点位移列阵    1 2 3  T  =    (2) 单元刚度矩阵 单元（1）：     (1) 0 0 0 1 T  = 3 2 3 2 2 2 (1) 3 2 3 2 2 2 12 6 12 6 6 4 6 2 12 6 12 6 6 2 6 4 EI EI EI EI l l l l EI EI EI EI l l l l k EI EI EI EI l l l l EI EI EI EI l l l l   −   − = − − − −   引入边界条件并换码： (1) (1) (1) 11 12 21 22 4 2 2 4 EI EI k k l l k k k EI EI l l       = =             单元（2）：     (2) 0 2 0 3 T  =

g k) 岂 下 引入边界条件并换码： k 单元(3)：{2}=[0003 「12E 6EI 12 P 是 12E 迎人杨T初丁 P 引入边界条件并换码： =k[ 单元(4)：{)=[0300 -12 是 覺 是 12E1 6EI 下！ 引入边界条件并换码： -kr-[T

3 2 3 2 2 2 (2) 3 2 3 2 2 2 12 6 12 6 6 4 6 2 12 6 12 6 6 2 6 4 EI EI EI EI l l l l EI EI EI EI l l l l k EI EI EI EI l l l l EI EI EI EI l l l l   −   − = − − − −   引入边界条件并换码： (2) (1) (2) 22 23 32 33 4 2 2 4 EI EI k k l l k k k EI EI l l       = =             单元（3）：     (3) 0 0 0 3 T  = 3 2 3 2 2 2 (3) 3 2 3 2 2 2 12 6 12 6 6 4 6 2 12 6 12 6 6 2 6 4 EI EI EI EI l l l l EI EI EI EI l l l l k EI EI EI EI l l l l EI EI EI EI l l l l   −   − = − − − −   引入边界条件并换码：   (3) (3) (3) 33 4EI k k l   = =     单元（4）：     (3) 0 3 0 0 T  = 3 2 3 2 2 2 (4) 3 2 3 2 2 2 12 6 12 6 6 4 6 2 12 6 12 6 6 2 6 4 EI EI EI EI l l l l EI EI EI EI l l l l k EI EI EI EI l l l l EI EI EI EI l l l l   −   − = − − − −   引入边界条件并换码：   (4) (4) (4) 33 4EI k k l   = =    

(3)结构刚度矩阵 「k,k 01 [K]=k" k) 0k22 7022 (4)等效结点荷载 0器 (5)结构刚度方程{P}=[K]{△ (6)解方程 2 320E 42-3 (7)求杆端弯矩 单元(1)： 4E副 -4320E7 39 M. 2 2 单元(2)： 1 M. '320E 单元(1)： M 器 0 -4320E 12.6(a) 试用先处理法计算图示桁架的内力和反力。各杆EA=常数

(3) 结构刚度矩阵   (1) (1) 11 12 (1) (1) (2) (2) 21 22 23 (2) (2) (3) (4) 32 33 0 4 2 0 2 8 2 0 0 2 12 k k EI K k k k l k k + + +         = =             （4）等效结点荷载   2 0 0 12 T ql P   = −     （5）结构刚度方程 P K  =     1 2 2 3 0 4 2 0 2 8 2 12 0 2 12 0 ql EI l                    − =                   （6）解方程 1 3 2 3 2 4 320 2 3 ql EI                 = −            （7）求杆端弯矩 单元（1）： (1) 3 1 2 2 4 2 0 2 3 2 4 4 320 80 EI EI M l l ql ql M EI EI EI l l             = =              − −        单元（2）： 2 (2) 3 2 2 2 3 4 2 3 4 12 80 2 2 4 1 320 3 12 10 EI EI ql M l l ql ql M EI EI EI ql l l          −             = + =                      − −             单元（1）： (1) 3 1 2 2 4 2 0 2 3 2 4 4 320 80 EI EI M l l ql ql M EI EI EI l l             = =              − −        12- 6 (a) 试用先处理法计算图示桁架的内力和反力。各杆 EA=常数

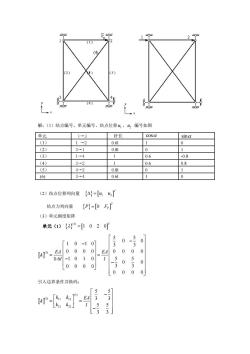
解：(1)结点编号、单元编号、结点位移私、山，编号如图 单元 ii 杆长 cosa sing (1) 12 0.6 (2) 3→1 0.8 (3) 1→4 1 0.6 -0.8 4} 3→2 1 06 0.8 (5) 4.2 08 (6) 3-4 0.61 (2)结点位移列向量{△}=[44] 结点力列向量 {P}=[0F (3)单元刚度矩阵 单元(1){}"=1020 「10-10] ["=0000E40000 Γ0.61-101015 L0000 3 09 0 L0000 引入边界条件并换码：

解：（1）结点编号、单元编号、结点位移 1 u 、 2 u 编号如图 单元 i→j 杆长 cos sin （1） 1 →2 0.6l 1 0 （2） 3→1 0.8l 0 1 （3） 1→4 l 0.6 -0.8 （4） 3→2 l 0.6 0.8 （5） 4→2 0.8l 0 1 (6) 3→4 0.6l 1 0 （2）结点位移列向量    1 2  T  = u u 结点力列向量   0  T P F = P （3）单元刚度矩阵 单元（1）     (1) 1 0 2 0 T  =   (1) 5 5 0 0 1 0 1 0 3 3 0 0 0 0 0 0 0 0 0.6 1 0 1 0 5 5 0 0 0000 3 3 0000 EA EA k l l   − −           = =       −   −           引入边界条件并换码：   (1) (1) 11 12 21 22 5 5 3 3 5 5 3 3 k k EA k k k l   −     = =         −    

单元(2){22=[0010 「00001 「00001 r-8-8 50 、 0-101J 0-0 4 引入边界条件并换码： [2-[0 单元(3){2"=[1000 「0.36-0.48-0.360.48 [k9-E4-048064 0.48 -0.64 1-0.360.480.36 -0.48 0.48-0.64 -0.480.64 引入边界条件并换码： ”=kP-和3 单元(1){2"-=[0020 「0.360.48-0.36-0.48 [=0480.64 -0.48-0.64 1-0.36-0.480.360.48 -0.48-0.640.48 0.48 引入边界条件并换码： [k=[k”-E03] 单元(5){2}2=[0020 「0000 「00001 [=4010-1 E0 4 0 -0.87000010000 0-101 引入边界条件并换码： [k]=[o]

单元（2）     (2) 0 0 1 0 T  =   (2) 0000 0000 5 5 0 0 0 1 0 1 4 4 0.8 0 0 0 0 0 0 0 0 0 1 0 1 5 5 0 0 4 4 EA EA k l l           − −   = =             −   −     引入边界条件并换码：     (2) k = 0 单元（3）     (1) 1 0 0 0 T  =   (3) 0.36 0.48 0.36 0.48 0.48 0.64 0.48 0.64 0.36 0.48 0.36 0.48 0.48 0.64 0.48 0.64 EA k l   − −   − − =     − −     − − 引入边界条件并换码：       (3) (3) 11 0.36 EA k k l = = 单元（1）     (1) 0 0 2 0 T  =   (4) 0.36 0.48 0.36 0.48 0.48 0.64 0.48 0.64 0.36 0.48 0.36 0.48 0.48 0.64 0.48 0.48 EA k l   − −   − − =     − −     − − 引入边界条件并换码：       (4) (4) 22 0.36 EA k k l = = 单元（5）     (2) 0 0 2 0 T  =   (5) 0000 0000 5 5 0 0 0 1 0 1 4 4 0.8 0 0 0 0 0 0 0 0 0 1 0 1 5 5 0 0 4 4 EA EA k l l           − −   = =             −   −     引入边界条件并换码：     (5) k = 0