山东理工大学：《画法几何与工程制图》课程PPT教学课件（十一五教材Ⅰ，机械制图第二版）第2章 几何元素的投影_第2章 几何元素的投影（5）综合问题

曾通高等教育“十一五”国家级规划敕材 SHANDONG UNTVERSITY OF TECHNOLOGY 机饿制图 少素承木到 第2章几何元素的投影 2.1投影方法 2.2点的投影 2.3直线的投影 2.4平面的投影 2.5几何元素的相对位置 2.6点、线、面综合问题解题示例

1 第2章 几何元素的投影 2.2 点的投影 2.3 直线的投影 2.4 平面的投影 2.5 几何元素的相对位置 2.1 投影方法 2.6 点、线、面综合问题解题示例

曾通高等教育“十一五”国家级规划教材 SHANDONG UNTVERSITY OF TECHNOLOGY 机饿制图 少素承之木军 2.6综合问题解题示例 2.6.1解题的一般步骤 ★ 分析题意 nn■a■a■aaa000aaa1■a01 BERNBEEn00nn1 ★ 确定解题的方法和步骤 ★投影作图 2.6.2 题目分类及分析方法 题目分类：相对位置题、距离题、角度题、综合题 分析方法 相对位置题：轨迹法和逆推法。 距离题（定距离和等距离)：轨迹法。 角度题：直角定理的应用。 综合题：轨迹法、逆推法、多种辅助方法

2 2.6 综合问题解题示例 2.6.1 解题的一般步骤 ★ 分析题意 ★ 确定解题的方法和步骤 ★ 投影作图 题目分类：相对位置题、距离题、角度题、综合题 2.6.2 题目分类及分析方法 分析方法 相对位置题：轨迹法和逆推法。 距离题（定距离和等距离）：轨迹法。 角度题：直角定理的应用。 综合题：轨迹法、逆推法、多种辅助方法

曾通高等教育“十一五”国家级规划敕材 SHANDONG UNTVERSITY OF TECHNOLOGY 机饿制图 少素承上大军 例：求点C到直线AB的距离，并求垂足K。 0 02 b的 解题步骤： 1.将线AB变换为投影面垂直线。将点C随之变换， a2 c2'就是点到线的距离。 2.由c1a与X轴平行得到，作投影连线求出k',k。 3

3 例：求点C到直线AB的距离，并求垂足K。 解题步骤： 2.由c1 k1与X2轴平行得到k1 ，作投影连线求出k′ 、k。 1.将线AB变换为投影面垂直线。将点C随之变换，a2′ c2′ 就是点到线的距离

曾通高等教育“十一五”国家级规划教材 SHANDONG UNTVERSITY OF TECHNOLOGY 机饿制图 少素承之木军 例：过点K作直线KL,使其垂直于交叉直线AB、CD。 b 1.过B点作BE∥CD,则 a AB和BE建立一个平面。 2.作KL⊥△ABE

b′ c′ d′ k′ a′ b c d k a 4 例：过点K作直线KL，使其垂直于交叉直线AB、CD。 e ● e ● ′ 1. 过B点作BE∥CD，则 AB和BE建立一个平面。 2. 作KL⊥△ABE。 ●l ● l′

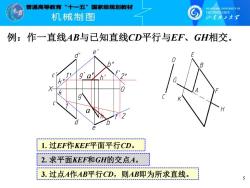
曾通高等教育“十一五”国家级规划敕材 SHANDONG UNTVERSITY OF TECHNOLOGY 机饿制图 少素承上木军 例：作一直线AB与已知直线CD平行与EF、GH相交。 1.过EF作KEF平面平行CD。 2.求平面KEF和GH的交点A。 3.过点A作AB平行CD,则AB即为所求直线

5 例：作一直线AB与已知直线CD平行与EF、GH相交。 1. 过EF作KEF平面平行CD。 3. 过点A作AB平行CD，则AB即为所求直线。 2. 求平面KEF和GH的交点A。 k′ k 1′ 2′ 1 2 a′ a b′ b

曾通高等教育“十一五”国家级规划教材 SHANDONG UNTVERSITY OF TECHNOLOGY 机饿制图 少东用之大军 例：求△ABC与△ABD之间的夹角 解题步骤： 1.将交线AB 变换为新投 X 影面的垂直线 b 两平面随之变换 3.角6即为所求 d1 b1 X1V19; aa(b2)

例：求△ABC 与△ABD 之间的夹角 解题步骤： 2.两平面随之变换 1.将交线AB 变换为新投 影面的垂直线 3.角 即为所求

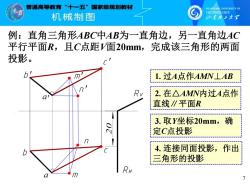
曾通高等放育 ”十一五”国家级规划敕材 SHANDONG UNTVERSITY OF TECHNOLOGY 机饿制图 例：直角三角形ABC中AB为一直角边，另一直角边AC 平行平面R,且C点距V面20mm,完成该三角形的两面 投影。 b 1.过A点作AMN⊥AB 2.在△AMN内过A点作 直线∥平面R 3.取Y坐标20mm, 确 定C点投影 b 4.连接同面投影， 作出 三角形的投影 RH 0 7

b′ b RH RV 7 例：直角三角形ABC中AB为一直角边，另一直角边AC 平行平面R，且C点距V面20mm，完成该三角形的两面 投影。 c′ ● 1. 过A点作AMN⊥AB 2. 在△AMN内过A点作 直线∥平面R c ● ●m ● m′ ●` n n′ ● 3. 取Y坐标20mm，确 定C点投影 4. 连接同面投影，作出 三角形的投影

曾通高等教育“十一五”国家级规划教材 SHANDONG UNTVERSITY OF TECHNOLOGY 机饿制图 少素承之木军 例：已知点M到△ABC的距离15mm,求m。 1.含点C在△ABC内作CD∥H面 CE∥面 2.含点C作CK⊥△ABC,即 ck⊥cd;c'k'⊥c'e' 3.用直角三角形法求CK实长， 并确定实长为15mm的水平投影 长，求出ff。 4.含点F作平面平行于△ABC GF∥BC,FH∥AB 5.在所作的平面内含点M作直线 GJ,在GJ上据m'求出m

m′ a′ b′ c′ a b c 4.含点F作平面平行于△ABC GF∥BC，FH∥AB 8 2.含点C作CK⊥△ABC，即 ck⊥cd； c′k′ ⊥ c′e′ 1.含点C在△ABC内作CD∥H面， CE∥V面 3.用直角三角形法求CK实长， 并确定实长为15mm的水平投影 长，求出f、f′ 。 5.在所作的平面内含点M作直线 GJ,在GJ上据m′求出m。 d′ d e e′ k k′ g′ f f′ g h′ h j′ j m 例：已知点M到△ABC的距离15mm，求m

曾通高等教育“十一五”国家级规划教材 SHANDONG UNTVERSITY OF TECHNOLOGY 机饿制图 少素用木军 例：已知直线DE、FG、HⅡ、JK。等腰△ABC的底边AB平行于 DE,且点A在FG上，点B在HI上，顶点C在JK上。完成△ABC 的两面投影。 1.含FG作平面FGM平行于DE 2.辅助平面法求作FGM与HⅡ的 交点，即点B 3.过点B作线平行于DE,交FG于 一 点，即点A。连接AB 4.用换面法将AB换为投影面平 行线，JK一起变换。点C在AB 的垂直平分面上，据此求得点C 5.连线得到△ABC两面投影

4.用换面法将AB换为投影面平 行线，JK一起变换。点C在AB 的垂直平分面上，据此求得点C 2.辅助平面法求作FGM与HI的 交点，即点B 1.含FG作平面FGM平行于DE 3.过点B作线平行于DE,交FG于 一点，即点A。连接AB 5.连线得到△ABC的两面投影 例：已知直线DE、FG、HI、JK。等腰△ABC的底边AB平行于 DE，且点A在FG上，点B在HI上，顶点C在JK上。完成△ABC 的两面投影。 c′ a′ b′ m′ a c b m