中南大学：《金属塑性加工原理》课程教学资源（PPT课件）第四篇 金属塑性变形力学解析方法 第8章 滑移线理论及应用

第8章 滑移线理论及应用 §8.1概述 §8.2平面应变问题和滑移线场 §8.3汉盖(Hencky)应力方程 滑移线 的沿线力学方程 §8.4滑移线的几何性质 §8.5应力边界条件和滑移线场的绘制 §8.6三角形均匀场与简单扇形场 组合问题及实例

第8章 滑移线理论及应用 §8.1 概述 §8.2 平面应变问题和滑移线场 §8.3 汉盖（Hencky）应力方程——滑移线 的沿线力学方程 §8.4 滑移线的几何性质 §8.5 应力边界条件和滑移线场的绘制 §8.6 三角形均匀场与简单扇形场 组合问题及实例

s8.1概述 滑移线理论是根据平面应变的变形力学特点，通过联 解精确平衡微分方程与精确塑性条件，求得理想刚塑性体 平面应变问题变形力以及变形区内应力分布的一种图解与 数值计算相结合的方法

滑移线理论是根据平面应变的变形力学特点，通过联 解精确平衡微分方程与精确塑性条件，求得理想刚塑性体 平面应变问题变形力以及变形区内应力分布的一种图解与 数值计算相结合的方法。 §8.1 概述

滑移线理论是二十 世纪二十年代初，基于 以下实验现象而发展起 来的：当金属进入塑性 变形的初期，人们可以 从光滑的金属试样表面 观察到一些规则取向的 条纹，即所谓的滑移 带”现象

滑移线理论是二十 世纪二十年代初，基于 以下实验现象而发展起 来的：当金属进入塑性 变形的初期，人们可以 从光滑的金属试样表面 观察到一些规则取向的 条纹，即所谓的“滑移 带”现象

实验表明，条纹上各点的切线方向正好是该点的最大 切应力方向。同时，金属塑性变形的微观机理研究表明， 这些条纹也恰好是金属晶体滑移变形的实际滑移面与金属 试样表面的交线，滑移线的名称即由此而来。据此，塑性 力学上把塑性流动平面内，最大切应力等于屈服切应力的 轨迹线称为滑移线。由于各点的最大切应力平面是成对正 交的，因此滑移线在塑性流动平面内为两族正交的曲线

实验表明，条纹上各点的切线方向正好是该点的最大 切应力方向。同时，金属塑性变形的微观机理研究表明， 这些条纹也恰好是金属晶体滑移变形的实际滑移面与金属 试样表面的交线，滑移线的名称即由此而来。据此，塑性 力学上把塑性流动平面内，最大切应力等于屈服切应力的 轨迹线称为滑移线。由于各点的最大切应力平面是成对正 交的，因此滑移线在塑性流动平面内为两族正交的曲线

实验表明，条纹上各点的切线方向正好是该点的最 大切应力方向。同时，金属塑性变形的微观机理研究表 明，这些条纹也恰好是金属晶体滑移变形的实际滑移面 与金属试样表面的交线，滑移线的名称即由此而来。据 此，塑性力学上把塑性流动平面内，最大切应力等于屈 服切应力的轨迹线称为滑移线。由于各点的最大切应力 平面是成对正交的，因此滑移线在塑性流动平面内为两 族正交的曲线

实验表明，条纹上各点的切线方向正好是该点的最 大切应力方向。同时，金属塑性变形的微观机理研究表 明，这些条纹也恰好是金属晶体滑移变形的实际滑移面 与金属试样表面的交线，滑移线的名称即由此而来。据 此，塑性力学上把塑性流动平面内，最大切应力等于屈 服切应力的轨迹线称为滑移线。由于各点的最大切应力 平面是成对正交的，因此滑移线在塑性流动平面内为两 族正交的曲线

由于金属塑性变形的基本机制是晶体在切应力作用 下沿着特定的晶面和晶向而产生滑移，滑移结果在试样 表面显露出滑移合阶，因此，滑移线是金属塑性变形时， 发生晶体滑移的可能地带。只有特定的晶面和晶向的切 应力达到金属的临界屈服切应力时才会使晶体产生滑移 变形

由于金属塑性变形的基本机制是晶体在切应力作用 下沿着特定的晶面和晶向而产生滑移，滑移结果在试样 表面显露出滑移台阶，因此，滑移线是金属塑性变形时， 发生晶体滑移的可能地带。只有特定的晶面和晶向的切 应力达到金属的临界屈服切应力时才会使晶体产生滑移 变形

现在，滑移线理论成为了求解理想刚塑性体平面应变问 题的重要方法之一，广泛应用于长宽比较大的矩形工件的平 锤压缩、宽板平辊轧制和板条平面挤压、拉拔等变形力和应 力分布的计算上。 近二十多年来，又推广到了主应力互为异号的平面应力 问题和轴对称问题等等方面

现在，滑移线理论成为了求解理想刚塑性体平面应变问 题的重要方法之一，广泛应用于长宽比较大的矩形工件的平 锤压缩、宽板平辊轧制和板条平面挤压、拉拔等变形力和应 力分布的计算上。 近二十多年来，又推广到了主应力互为异号的平面应力 问题和轴对称问题等等方面

ds. §8.2平面应变问题和滑移线场 对于平面塑性流动问题，由于某一方向上的位移分量为零 (设duZ0) ,故只有三个应变分量(dex、dey、dyg) 也称平面应变问题。平面应变问题的最大切应力为 t=(o1-03)/2=V(ox-o,)/2]+ 这是一个以tmax为半径的圆方程，这个圆便称为一点的 应力状态的莫尔圆

§8.2平面应变问题和滑移线场 对于平面塑性流动问题，由于某一方向上的位移分量为零 （设duZ=0），故只有三个应变分量（ 、 、 ）， 也称平面应变问题。平面应变问题的最大切应力为： d x d x  x d d y  d xy  2 2 max 1 3 ( )/ 2 [( )/ 2] x y xy  =  − =  − + 这是一个以τmax为半径的圆方程，这个圆便称为一点的 应力状态的莫尔圆

a b C 图8-1平面应变问题应力状态的几何表示 (a)塑性流动平面（物理平面）， (b)Q:证交曲线坐标系的应力特点， (c)应力莫尔圆

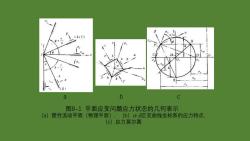
图8-1 平面应变问题应力状态的几何表示 （a）塑性流动平面（物理平面），（b）α-β正交曲线坐标系的应力特点， （c）应力莫尔圆 a b c

根据平面流动的塑性条件，Tmx=K(对Tresca塑性条件k= G/2;对Mises塑性条件k=o,/3 由图8-1(C)的几何关系可知，有 ox=-p-ksin2Φ oy=-p+ksin2Φ ty=kc0s2Φ 式中静水压力p(=-om=(ox+o,)/2) 中一定义为最大切应力tmx(仁k方向与坐标轴Ox的夹角

根据平面流动的塑性条件， τmax = k（对Tresca塑性条件k = σT /2；对Mises塑性条件 由图8-1(C)的几何关系可知，有  x = − p − k sin 2  y = −p + k sin 2  xy = k cos 2 式中静水压力 Ф——定义为最大切应力τmax (= k)方向与坐标轴Ox的夹角 k =  T / 3 ( ( ) / 2) p = − m = −  x + y